早稲田大学商学部数学の勉強法、対策について
商学部の数学は空所補充形式解答と記述式解答で、結果だけでなくそれに至るまでの過程を書く記述力が求められます。全て解き切るのは時間的にあまり余裕がないので、手際よく正確に解いていくことが大切になります。
ページ目次

- 【何からはじめたらいい?という人向け】
【まず始めることをお伝えします】 - 早慶に合格するための戦略とは?
1,2年生から合格するための戦略を立てるには? - 【高1】早慶現役合格の勉強法を徹底解説
志望校に合格するためにやるべきこと紹介 - 【高2】現役で早慶GMARCHに合格
必要な勉強法(勉強時間、参考書)を紹介 - 【高2】早慶絶対合格!!のためにすること
勉強時間、スケジュール、参考書、勉強法の紹介
早稲田大学商学部数学の全体概観
配点60点 時間90分
例年大問は3問で、[1]は小問、[2],[3]では記述式になっています。
早稲田商学部数学の出題範囲・頻出分野
出題範囲は数学ⅠAⅡB(確率分布と統計的推測を除く)となっています。
頻出分野は数列、ベクトル、図形と三角関数、三角関数、微積分、整数問題です。
近年整数問題の出題頻度が非常に高く、難易度も文系ではトップレベルに難しいです。
また微積分ついては2014、2016年度の[2]で出題されています。
難易度については基礎から応用まで幅広く出題されています。本質的な理解を問う問題や思考力を問う問題が出されるのも特徴です。
早稲田商学部数学の対策
早稲田商学部数学の問題を解いていくにあたって、どのように考えていくのが良いのかをお伝えしていきます。

基礎問題の演習
文系学部としては、かなり難しく準備を十分にできたかどうかで差がつくといえます。
そのため、数学受験の人は十分に準備してください。
数学力を身につけることが大事となりますが、そのためには基本的な問題が解けるようになることが重要です。公式を単純に適用する問題が少なく、基本事項を本質的に理解していないと対応できない問題が多いので、公式を覚える際にはどの定義から導き出されてどのように公式を使うのかを常に考えながら問題演習をしていくのが良いでしょう。
こうした思考をすることで、後々応用問題を解く際にも役に立つ論理力を身につけることができます。

頻出分野の問題演習

- 早慶は浪人しても難しい!?
根本的に変えていく必要性とその方法を伝授 - 【早慶浪人】伸びないのはなぜ?
伸ばし方を説明 - ヒロアカの浪人生必勝必勝コース
基礎から合格するための勉強法 - 【早慶浪人】年間スケジュール
浪人生が早慶に合格するための計画の立て方とは - 【早慶】女子浪人が絶対に合格には
志望校に合格するためにやるべきこと紹介 - 【早慶】3月にやっておくこと
早慶を目指す浪人生が絶対に3月にやっておくことを紹介
出題範囲を満遍なく勉強をすることは当然として、頻出分野は特に意欲的に問題演習をしていく必要があります。特に数列、微積分、場合の数・確率、三角関数は得意分野になっているようにしておきましょう。
整数問題についても頻出分野となっています。勉強しにくい分野ですが基本パターンは存在するので、習熟しておくと良いでしょう。先述の通り、早稲田商学部ではかなり難度の高い整数問題が出題されます。試験時間との兼ね合いから完答する受験生は限りなく少ないでしょうから部分点を稼ぎにいくスタイルでいいと思います。問題もガウス記号、不定方程式、格子点と様々ですから対策はしにくいです。
またベクトル、図形と方程式も頻出分野です。この分野については図やグラフを実際に書いてイメージを養うトレーニングをしていくのが良いでしょう。

記述式と同様に考えて解答作成の練習をする
答えのみの回答だからといって記述練習を怠るのではなく、普段から途中式や導出過程、細かい条件まで含めた解答作成を心がけましょう。
記述式では答えより答えに至るまでの道筋の方が重要視されます。答えがあっていたとしても、記述がめちゃくちゃなら点数はほとんど0に等しいと思った方がいいです。
循環論法に気を付けたり、必要十分性を常に考えながら議論を進めると論理の穴は少なくなるでしょう。
というものの記述の大問2、3は文系にとっては難しく、ほとんど差がつかないことが予想されます。
ある程度議論に飛躍や不備があったとしてもあまり気にせず、答えまでの考え方や論述の骨組みを明確に示し、他の受験生との差別化を図るのも作戦です。自分で色々シュミレーションして本番に備えると大きな失点は防げるとおもいます。

速く正確に解くための計算力をつける
大問が3題で60分と、1問あたりにかけられる時間は単純計算で20分です。問題量や難易度を考えると決して余裕があるとは言えません。そのため、迅速かつ正確な計算力が必要となります。日ごろの問題演習で要領よく正確に計算していくとともに、最後の答えまでたどり着けるように練習していきましょう。
過去問を解く際には・・・
問題演習に慣れてきたら、実際に過去問に取り組みましょう。この際、本番通りの時間で解くことが大切です。数学ではどの分野が何問目に出るかが分からないので、時間を測って問題演習をし、自分が解きやすいと思った問題から解き始めることが重要です。
あまり1つの大問を完答することにこだわりすぎるとかえって点数が下がってしまいます。大問前半の比較的易しい問題を確実に解答することで、得点を伸ばしていきましょう。ただし、時間内に解けなかった問題もその後に問題演習として解くことも大事です。時間内に解けなかった問題は必然的に苦手な問題であるため、苦手をつぶす意味でも解けなかった問題の復習をしましょう。
早稲田大学商学部数学の出題例から考える

小問集合の問題です。
(1)まず、(ii)の式を実際に解いてみましょう。
![Rendered by QuickLaTeX.com n= \int_ {a_{n} }^ {a_{n+1}} (x+ \frac{1}{2} ) dx\\= \frac{1}{2} \int_ {a_{n} }^ {a_{n+1}} (2x+ 1 ) dx\\= \frac{1}{2} \left[x^2+x\right]^ {a_{n+1}} _ {a_{n}}\\ = \frac{1}{2} \big( a^{2} _{{n+1}}+ a_{n+1}- a^{2} _{{n}}- a_{n} \big) \\\therefore a^{2} _{{n+1}}+ a_{n+1}- a^{2} _{{n}}- a_{n} =2n](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-afbf87662f28b3aafe953268b76c29a8_l3.png)
となります。実際にこのように積分してもいいのですが、被積分関数が一次関数なのでこの積分は要するに台形の面積を求めろということなので、実際にそれをイメージして解くのもいいでしょう。
次に漸化式が求まったので、実際にn=1から調べてみましょう。

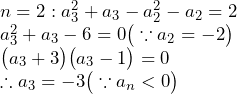
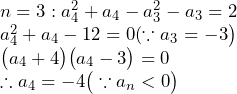
この時点で![]() であると予想できます。答えも
であると予想できます。答えも![]() です。
です。
本来なら数学的帰納法を使って証明してから答えを埋めるべきでしょうが、本番だったら答えを書いて時間があれば証明してみるといいと思います。
帰納法で証明についてはここでは割愛します。
(ii)∑のままだと今回計算が進まないので、Σをばらしましょう。
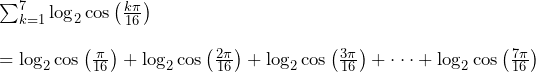
ここで、前から順番に足していくのはあまりいい方法ではありません。
今回対数と三角関数が絡んでいます。
・対数はlogA+logB=logAB
・三角関数同士の足し算、掛け算は三角関数で書ける(和積、積和公式のこと)
・三角関数はsin,cosは位相をずらせばどっちでも書ける
という性質があります。
その性質を考えたうえで以下の式変形を考えるとこうするべきというのがお判りでしょうか?

次に{ }の中の後ろにあるcosをsinで書き換えてみましょう。そうすると倍角の公式が公式が使えるというのが見えてきます。
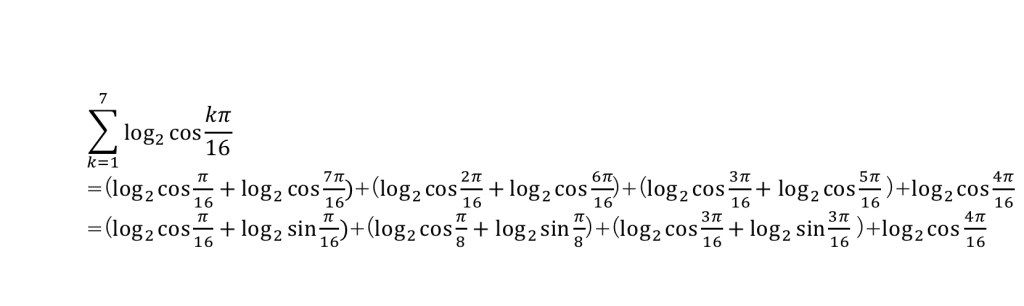
倍角の公式を使うと
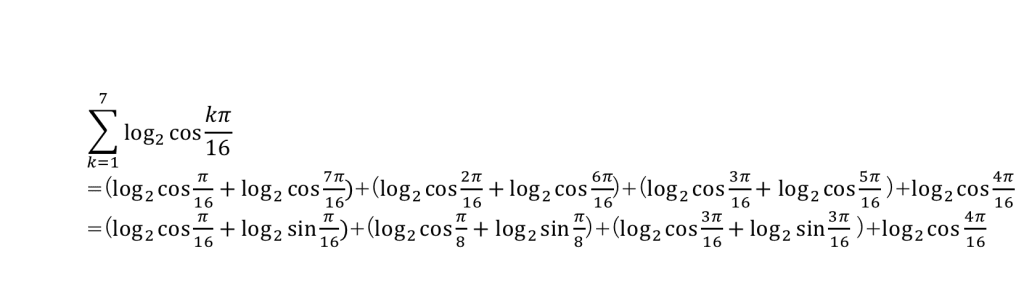
(与式)![]()
対数の中身をばらしてまとめると
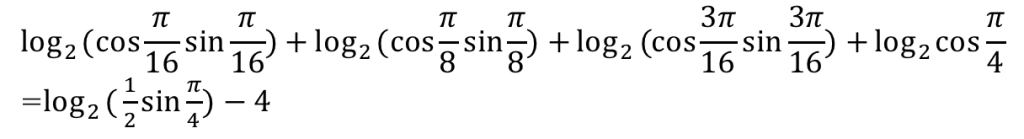
![]()
となります。
早稲田商学部に合格するための参考書
当塾で使用していて早稲田大学商学部に合格へ必要な参考書を紹介します。もちろん、当塾の場合は一人一人個別にカリキュラムを作成するため下記のようなカリキュラムは一例となります。参考書は何をやるかよりも、どのような目的で使用するかというが大事です。闇雲に行って情報量に圧倒されてしまうのではなく、1つ1つ目的意識を持って勉強していきましょう。
早稲田大学商学部に圧倒的な実力で合格できる専門対策をします
まずは資料請求・お問い合わせ・学習相談から!
早慶専門個別指導塾HIRO ACADEMIAには、早稲田大学専門として商学部への圧倒的な合格ノウハウがございます。
少しでもご興味をお持ちいただいた方は、まずは合格に役立つノウハウや情報を、詰め込んだ資料をご請求ください。
また、早稲田大学商学部に合格するためにどのよう勉強をしたらよいのかを指示する学習カウンセリングも承っています。学習状況を伺った上で、残りの期間でどう受かるかを提案いたしますので、ぜひお気軽にお電話いただければと思います。
⇒ 早稲田大学・商学部に合格したい方は、まずは当塾の資料をご請求ください。


















Published by