早稲田大学教育学部が2/19に入試を迎えました。 このブログ記事では英語の問題を分析していきます。 ページ目次2024年早稲田大学教育学部英語全体講評2024年早稲田大学教育学部英語大問Ⅰ2024年早稲田大学教育学部英語大問Ⅱ2024年早稲田大学教育学部英語大問Ⅲ2025年早稲田大学教育学部を受ける

• …続きを読む
• 早稲田大学教育学部が2/19に入試を迎えました。

  このブログ記事では英語の問題を分析していきます。

  2024年早稲田大学教育学部英語全体講評

  

  近年早稲田教育学部は大きくレベルが上がり、
  今年度も同じ形式で出題されました。

  昨年ほどの長さではなかったのですが、
  文章自体が平均で1000wordsと長いので、読むのが大変です。

  問題自体はパラグラフで解ける問題がほとんどで、解ける問題を解けるようにして欲しかったです。

  [toc]

  解答作成には万全を期していますが、間違えている可能性は十分にありえます。速報ですので、参考程度に留めておいてください。少しですが解説・考え方も載せていますので参考にしてください。
  重要：大学側から配点が公式に発表されてませんので、どれくらいあっていたら合格できるかはわかりません。

  2024年早稲田大学教育学部英語大問Ⅰ

  1 b
  2 a
  3 b
  4 d
  5 c
  6 b
  7 c
  8 b
  9 c
  10 a
  11 a
  12 d
  13 b
  14 b

  解答根拠

  (1)

  傍線内の比喩表現を理解する必要がある問題です。
  本文の最後の部分である「goodness, the difference between right and wrong, the nature of fairness — are sunk in conceptual quicksand」というフレーズが示しているのは、”善良さ、正と不正の違い、公平性の本質といった概念が概念上の流砂に沈んでいる”、
  つまりこれらの日常的な概念が本質的に定義が困難であるという意味です。これは、第2段落の最後の文に該当します。

  選択肢(a)「これらの考えは非常に特異である」には根拠がありません。文章中でこれらの概念が特異であるとは述べられていません。

  選択肢(c)「共通の考えが文化を超えて普遍的な意味を持たない」という意見も文章から直接導き出すことはできません。文化間の普遍性については言及されておらず、概念が深い理論的な混沌に陥っているという点に焦点を当てています。

  選択肢(d)「これらの考えが日常会話で見つけるのは非常に珍しい」という選択肢も文章の内容とは合致していません。むしろ、子どもたちが日常的にこれらの言葉を使っていると述べており、それは日常会話でよく使われる概念であることを示しています。

  (3)

  選択肢(b)「公平さの理論を説明する」が、下線部(3)「その瞬間の特定のコミュニケーションの課題」としては例として挙げられないものです。

  この文章は、「公平さ」や「善良さ」といった抽象的な概念について、哲学者たちが普遍的な理論を提供しようと苦闘している一方で、子供や大人はその瞬間のコミュニケーションの課題に対処するために十分に明確な意味を理解するだけでよいと述べています。具体的には、「It’s not fair!」と叫ぶことで子供が感じている不公平感を表現する必要がありますが、そのために全般的な公平さの理論を心に留めておく必要はないと説明しています。これは、本文の第2段落の第2文から第5文にかけての記述です。

  選択肢(a)「自分が何を望んでいるかを表現する」、選択肢(c)「自分の感情を伝えるための正しい言葉を見つける」、選択肢(d)「もっと大きなケーキのピースを求める」という行為は、いずれもその瞬間における特定のコミュニケーションの課題対する対処と見なすことができるため、下部(3)の例として適切です。

  (4)

  文章の中で、「fairness」（公平さ）についての明確な定義を提供している部分はありません。
  哲学者たちが「公平さ」を含む深い概念の普遍的な理論を構築しようとする挑戦について語っており、それがどのような状況や文脈でも機能するようなものでなければならないと述べています（第2段落の第1文）。
  しかし、子供たちや大人は、その瞬間、その瞬間の特定のコミュニケーションの課題に対処するのに十分な意味を捉えるだけで良いとも説明されています（第2段落の第2文と第3文）。
  例えば、「It’s not fair!」という叫びが子供がケーキの小さい切れ端を渡されたり、列で待たされたりしたときの憤りを表現する必要があるとされていますが、これは公平さの一般的な理論を心に留めておく必要はないとされています（第2段落の第4文と第5文）。

  選択肢(a)「全員がケーキの等しい部分を受け取ること」、選択肢(b)「贔屓なく公正な扱い」、選択肢(c)「プリスクールの子供たちが一人ひとり順番に列に並ぶこと」は、文章中で「fairness」の定義として明確に提供されているものではありません。

  (5)

  ここではエリザの例から、「子どもたちの概念理解における矛盾」を示すために使われていることがわかります。
  例えば、エリザがおもちゃの熊について言及している部分では、彼女は次のように述べています:
  “E: No —she’s dead. HOW CAN THAT BE?”
  “E: No, she’s middle-sized in between alive and dead. She moves sometimes.”（第3段落）。

  エリザが生きているものと死んでいるものの間の概念的な矛盾に直面していることを示しています。
  彼女の理解では、おもちゃの熊は動くことがあるため、「生きても死んでもない中間の状態」にあると解釈しています。

  さらに、エリザが死んだ人々の行動についての誤解を示す部分では、彼女は次のように質問します:
  “E: How do dead people go to the bathroom?”
  これに対して、「S: Dead people don’t have to go to the bathroom. They don’t do anything; they just lie there.」と応答されますが、
  エリザはそれでもなお、「E: But they ate or drank before they died — they have to go to the bathroom from just before they died.」と返答します（第3段落）。

  これらの引用は、子どもたちが生と死の概念をどのように理解し、それに疑問を持っているかを明確に示しています。
  彼女の疑問は、生きているものと死んでいるものの定義に関する成人の概念とは異なる、独自の解釈を反映しています。

  (6)

  b「Things that do not move or cannot be seen are not alive」がエリザの生と死に関する理解に最も適していると考えられます。これは、エリザが生きているものと死んでいるものをどのように区別しているかを示す文から明らかです。

  エリザがテレビで撃たれた人について言及した際、「”He’s dead — I can tell because he’s not moving.”」と述べています（第3段落）。この発言は、動かないものは生きていないというエリザの基本的な理解を示しています。
  さらに、エリザは、「”Isn’t it funny — statues aren’t alive, but you can still see them?”」と発言しています（第3段落）。この発言からは、エリザが見えるが動かないもの、この場合は像を、生きていないものと認識していることがわかります。

  これらの点から、エリザの生と死の理解は、動きや見えるかどうかに基づいていることが示されています。
  このため、bが彼女の観点を最もよく表していると考えられます。

  他の選択肢については、本文から確認できません。
  a「Statues are alive when you do not look at them.」は、エリザの観察からは支持されません。彼女は像が生きていないと認識していますが、見るか見ないかに基づくという考えは示されていません。
  c「People who are shot on TV are not real, and cannot die.」については、エリザがテレビ上での死を現実の死と同じように解釈していることから、この選択肢は彼女の理解を反映していないと言えます。
  d「Life and death are the same thing.」はエリザの観察に反するものです。彼女は生と死を区別しようとしており、それらが同じだとは考えていないようです。

  (8)

  この文脈での「charades」は、言葉を使った遊びやゲーム、特にコミュニケーションの状況において使用される比喩的な表現を指しています。
  第7段落で、「Both pre-school children and adults use words as players use gestures in charades — in creative, contradictory ways that are good enough to get through the language games of the moment.」と述べられています。
  ここでは、「charades」という言葉が、言語を使用したゲームや遊びを指していることを示しています。
  具体的には、子どもたちと大人が言葉を使って創造的かつ矛盾する方法でコミュニケーションを取り、その瞬間の言語ゲームを成功させることを指しています。

  a「language changes」はこの文脈では適切ではありません。「charades」が言語の変化や進化を指しているという直接的な証拠は文中にありません。
  c「sign languages」もまた、この文脈においては不適切です。文章は手話や特定のサイン言語を指しているのではなく、一般的なコミュニケーションの文脈での言語使用について語っています。
  d「language signs」も正確な表現ではありません。「charades」は言語の記号やサインを直接的に指すのではなく、言葉を使った遊びやゲーム、コミュニケーションの戦略を示しています。

  (10)

  第5段落では、生命の定義に関して「But this leaves tricky cases such as viruses (not composed of cells, not able to reproduce independently), viroids (circular RNA strands that replicate autonomously inside a host plant), prions (infectious proteins), and even the androids of the future (could a machine be conscious without being alive?). The definition of life, like the definitions of good, justice, right and wrong, has been the subject of endless and unresolved debates for millennia.」と述べられています。
  この引用は、生命の定義に関する質問が複雑であり、簡単な答えが存在しないことを示しています。

  b「questions that no philosophers have considered」は不正確です。文中で哲学者がこれらの問題を考慮していないとは言及されておらず、むしろ「endless and unresolved debates for millennia」と述べられています。
  c「questions that only scientists can answer」も不正確です。文中で科学者だけがこれらの問題に答えられるとは述べられておらず、実際にはこれらの質問が長い間議論されてきたことが示されています。
  d「questions with clear spiritual and religious answers」も文脈に合っていません。第5段落では、生命の定義に関する質問が宗教的または霊的な明確な答えを持っているとは述べられておらず、むしろこれらの問題が未解決のままであると説明しています。

  (11)

  第6段落には、「These types of questions(5段落の内容) are mostly irrelevant in the vast majority of linguistic charades we play in everyday communication — the tricky cases just don’t arise much in ordinary conversation. What matters is that we can get along well enough when dealing with the situations that actually occur in daily life.」と記述されています。この引用は、日常生活でのコミュニケーションでは、哲学的な意味の問題がほとんど関係なく、実際に発生する状況を上手く扱えることが重要であるという著者の主張を明確にしています。

  b「We need to memorize the definitions of words that other people use」については、第6段落では他人が使用する単語の定義を暗記する必要性について言及していません。
  c「People have numerous reasons to negotiate the meanings of life and death」も、この段落の主なメッセージではありません。実際には、日常会話では生と死の意味について交渉する多くの理由があるとは述べられていません。
  d「Children’s games are an important part of learning about life and death」に関しては、第6段落では子どものゲームが生と死について学ぶ重要な部分であるとは特に言及されていません。

  (12)

  第6段落「We no more need a mental definition of life to talk about living relatives or dead pets than we need a biological definition of gorillas to mime King Kong.」
  no more のいわゆるクジラ構文です。

  これは、生きている親族や亡くなったペットについて話す際に、生命の厳密な定義が必要でないのと同じように、キングコングを真似るためにゴリラの生物学的な定義を必要としないことを示しています。このアナロジーは、特定の活動やコミュニケーションにおいて、高度な専門知識よりも、状況を処理するための基本的な理解がより重要であることを強調しています。

  a「an understanding of the planet Mars to study the sun」は、太陽を研究するために火星の理解が必要でないという点でアナロジーが成立するものの、日常的な活動やシンプルなタスクと直接的な関連性が薄いため、この文脈でのアナロジーとしては適切ではありません。
  b「the classification of pipes to play the videogame Super Mario Brothers」は、ビデオゲームをプレイする際に特定の分類知識が必要でないという点で面白い比喩ですが、本文のコンテキストにおいて生命やコミュニケーションのシンプルさを示すアナロジーとしては直接的ではありません。
  c「the meaning of gorillas to say that they are 200 kilogram primates」は、本文引用部分に実際に登場するゴリラに関するアナロジーを使っていますが、この選択肢はアナロジーそのものを説明しており、置き換えるアナロジーとしては機能しません。

  (13)

  下線の表現は、コミュニケーションの過程で表面上は見えないが、実際の意味や理解に影響を与える大きな要素を指しています。

  第7段落から解答の根拠を具体的な引用すると、「And playing those conversational games requires paying attention to likely communicative objectives, the contents of the environment, and past linguistic usage — the hidden parts of the communication iceberg are just as important as the words themselves.」です。
  これは、会話ゲームをする際には、コミュニケーションの目的、環境の内容、過去の言語使用といった、一見すると見えないコミュニケーションの側面に注意を払う必要があると述べています。これらの「隠された部分」は、言葉自体と同じくらい重要であると強調しています。

  a「the differences in mother tongue that are a titanic obstacle to communication」は、文中で特に言及されているわけではなく、bのように広範なコミュニケーションの側面を包括しているわけではありません。
  c「the communication between children and adults that is often deep, cold, and damaging」は、第7段落での表現や文脈とは異なり、コミュニケーションの隠れた側面を説明する際に使用されているメタファーに合致しません。
  d「the true intentions that are not revealed in intergenerational communication」も、隠れた部分を指すメタファーとしては適切ではありますが、第7段落で述べられている「隠された部分」の説明はもっと広範なコミュニケーションの要素に関連しています。
  したがって、bが「the hidden parts of the communication iceberg」の意味を最も正確に反映しており、コミュニケーションの過程で見えない、しかし重要な部分を指しています。

  (14)

  記事全体を通じて、日常のコミュニケーションにおいて人々が共有する意味や概念は、その場その場のコンテキストに基づいて適応的に理解され、交渉されることが強調されています。第2段落で、「But children and adults only have to get meaning sufficiently clear to deal with the specific communicative challenge of the moment.」と述べられています。これは、日常のやり取りの中で人々が意味を常に交渉していることを示しています。

  a「People are able to communicate clearly using words because we already share a common understanding」は、記事が示すコミュニケーションの複雑さを過小評価しています。共有された理解があるとはいえ、その理解は状況に応じて変化し、交渉されることが強調されています。
  c「Young children play charades because they are not good at using language the same way as adults」は、子どもたちの言語使用に関する記事の主旨を誤解しています。実際には、子どもたちが成人とは異なる方法で言葉を使う能力について議論しつつ、それがコミュニケーションの交渉の一環であることを示しています。
  d「People in different countries use different nonverbal strategies to communicate when they lack the vocabulary to speak」は、この記事の焦点ではありません。記事は、非言語的戦略よりも言葉を使った意味の交渉に重点を置いています。

  出典

  “The Language Game: How improvisation created language and changed the world”

  by Morten H. Christiansen , Nick Chater

  2024年早稲田大学教育学部英語大問Ⅱ

  1 c
  2 b
  3 d
  4 d
  5 a
  6 b – a
  7 a
  8 a
  9 c
  10 d

  解答根拠

  (1)

  第1段落の最後の文から明らかです。「the invention of the first device ever that permitted us to henceforward stop using a part of our brains」では、Cal-Tech電子計算機が私たちが脳の一部を使うのを止めることを可能にした最初の装置であると著者が考えていることを示しています。

  aについては、著者が1967年に感傷的である、またはその年を特別なものとして懐かしんでいるという明確な証拠は文中にありません。
  bに関しては、Cal-Tech電子計算機の「impeccable accuracy」について第2段落で言及されていますが、それが著者が詳細に議論する主な理由ではないことが第1段落で示されています。
  dについては、電子計算機が私たちの生活を容易にしたという事実は第2段落で示唆されていますが、これが著者がCal-Techについて詳細に議論する主な理由ではなく、むしろ脳の使用を減らすことの影響に焦点を当てているためです。

  (2)

  第2段落「they still required you to make some use your grey matter; the Cal-Tech freed you up entirely」という部分で、Cal-Tech電子計算機が人々を「grey matter」、つまり脳胞を使う必要から解放したと述べています。この文脈で「grey matter」は脳の活動、特に計算を行う際の脳細胞の使用を指していると解釈できます。

  a「arithmetical instinct」についは、本文中では直接的に算数的直感につて言及されていないため、これを「grey matter」と考えるのは適切ではありません。
  c「vague ideas」も同様に、本文中で脳の活動や思考としての「vague ideas」につては言及されておらず、論理的な対応物は考えられません。
  d「electronic calculatorは、Cal-Tech 電子計算機が人々を脳細胞をう必要から解放したという文脈で言及されています、これは「grey matter」の代替というよりは、その使用を不要にしたツールと述べられています。したがって、これも「grey matter」の置き換えとしては適していないと言えます。

  (3)

  この選択肢を選んだ理由は、第6段落における「This has in recent months led to widespread hand-wringing. Our minds, it is said, will inevitably fall out of use, atrophying, or distending, whichever is worse」という文から明らかです。ここで表現されている「widespread hand-wringing」とは、人々が電子計算機やその他の技術革新が私たちの脳を使う方法に及ぼす影響について広範囲にわたって心配していることを指しています。

  aについては、長文のどこにも日々の忙しい作業が手に影響を与えるという心配に関する言及はありません。
  bに関しても、疲れるほどの精神的作業に関する心配が直接的に表現されているわけではなく、著者が言及しているのは、私たちが脳を使用する必要がなくなるという懸念です。
  cは、ディストピア的なビジョンが私たちに汚染された世界を放棄させるかもしれないという心配について述べていますが、これは第7段落の映画「Wall-E」の描写に基づく例えであり、直接的な心配の原因としては言及されていません。

  (4)

  この選択肢を選んだ理由は、第7段落と第8段落に基づいています。第7段落で、著者は「Wall-E」という映画を引き合いに出して、物理的な怠惰がもたらすディストピア的な未来像を描いています。引用すると、「the nightmare model – for our bodies – is a movie like Wall-E」とあります。そして直後の第8段落では、「So now there comes a similarly dire vision for our minds」と続けており、これは映画で描かれた身体の未来に対する悲観的な視点と精神の未来に対する悲観的な視点を比較していることを示しています。

  aについては、著者が「Wall-E」を引用しているのは夢を見ることに関する警告のためではなく、未来に対する一般的な悲観的なビジョンを示すためです。bについては、著者は実際に人々が映画のような生活をすることに対する心配を表明しているわけではなく、比喩的な意味で映画を参照しています。cは、映画で起こったことが現実の人々の心に起こると著者が確信しているように解釈される可能性がありますが、著者は比較を行っているに過ぎず、必然性を主張しているわけではありません。

  (7)

  下線部はthoughの倒置になります。意味が同じなので、asの倒置よりもわかりやすいとは思いますがGeniusの引用をしておきます。

  ⑸［倒置される場合］ 倒置した Late though it was, the meeting still continued. （遅くなったが, 会議はまだ続いていた）の語順で用いるのは｟主に文｠. この場合にthough ではなくalthoughを使うのはきわめてまれ（→as接6a））. 名詞句が前置された場合は無冠詞となる：Genius though he was, he had no common sense. 彼は天才だったが, 常識というものがなかった. 動詞（句）の前置は｟やや古｠：Fail though I did, I would not give up my dream. 失敗したが夢はあきらめない.
  出典：Genius6 though　部分

  ここで著者は、AIによる変革がもたらすであろう知的生活に対する楽観的なビジョンを提示しており、同時に自身の見解が空想的に聞こえるかもしれないと予想しています。これは、著者がそのビジョンに対する批判や懐疑的な反応を予測していることを示唆しています。

  bは、著者が「renewed innocence」について疑念を抱いているとは文中で示されておらず、むしろそのような状態の到来を期待しているように読み取れます。
  cは著者がアリストテレスの関連性について不確かであるかのように語っていますが、文脈からは著者が古代ギリシャの知識人に言及しているのは、彼らが持っていた知の純粋さを現代でも追求すべきだという示唆のためであり、その関連性を疑っているわけではありません。
  dは、AIが新たな哲学者の出現を引き起こすと著者が考えているかのように読めますが、その表現は第15段落において「Fanciful though it may sound」という前置きを経て、可能性の一つとして提示されているに過ぎません。

  (8)

  第12段落で著者は古代ギリシャの知識人の心について言及していますが、「Their minds, though steeped in the totality of contemporary knowledge, were thus almost tabulae rasae – nearly empty, ready to take it all in, ready to think, primed for purpose.」と述べています。これは、古代ギリシャの知識人の心が、当時知られていた知識によって満たされていたが、まだ知られざることが多く、新しい情報を取り入れる準備ができているという意味です。現代の心が「ほとんど空」とはどこにも書かれていません。

  bについては、第4段落において「GPS has given us all the direction we might ever need.」と述べられており、GPSが従来の方位を測るツールを置き換えたことが明示されています。
  cは第14段落に基づいており、「a more reasonable sound-to-noise ratio, gifting us with a renewed innocence」とAI技術によって知的生活が改善される可能性が示唆されています。
  dは第2段落で、電子計算機がアバカスや計算尺とは異なり、完全に自動化されていて使い者の心を使う必要がないと説明されています。「The abacus and the slide rule might have been mental labour-saving devices, but they still required you to make some use of your grey matter; the Cal-Tech freed you up entirely.」

  (9)

  第13段落と第14段落に基づいています。著者は「Which is why our modern minds, once they have been purged of all that today’s algorithms might now deem unnecessary information, will be as ready as theirs were to think, to inquire, to wonder, to contemplate, to imagine, to create.」と述べています。これはAIが不必要な情報を取り除くことで、私たちの知的能力をより完全に行使することを可能にするという著者の楽観的な見解を反映しています。
  さらに著者は「So I see today’s algorithmic revolution as a necessary cleansing, a movement by which we rid ourselves of all the accumulated bricolage of modern intellectual life, returning us to a more reasonable sound-to-noise ratio, gifting us with a renewed innocence, filled with potential.」とも述べており、これもAIの肯定的な影響に対する彼の見方を示しています。

  aについては、著者がAIによって人間が怠惰な夢想家になることを恐れているという直接的な証拠はありません。第9段落で著者は「But I am not a doomsayer – not so far as our minds are concerned, at least.」と述べており、これは彼がAIに対して恐れを持っているわけではないことを示しています。bに関しては、著者がAIに関して全く懸念を抱いていないわけではないものの、第9段落での言及は、AIに関する彼の全体的な姿勢が楽観的であることを示しています。dは、著者がAIアルゴリズムが古代ギリシャの哲学者たちの独創性を超えると考えているかのように読めますが、文中ではそうした比較を行っていません。

  出典

  The big idea: will AI make us stupid?

  2024年早稲田大学教育学部英語大問Ⅲ

  1 c
  2 c
  3 c
  4 b
  5 c
  6 a
  7 d
  8 a
  9 b
  10 b
  11 d
  12 a
  13 d

  解答根拠

  (4)

  b「Terminal lucidity occurs when neural networks that were regarded as damaged are restored.」が本文の記述と一致しないという主張は、文中の情報とは合致しません。これを説明するためには、4段落の「It suggests there may be neural networks that are remaining, and/or pathways and neural function, that could help potentially restore cognitive abilities to individuals we otherwise think are permanently impaired」という部分を引用します。
  この文は、損傷したと考えられていた神経回路が復活するということではなく、依然として残っているかもしれないと可能性を示唆しています。
  これは神経回路が復元されるというよりは、まだ機能している神経回路が存在すること示されているため、bは文の内容とは一致しせん。

  a. 5段落「research into this phenomenon is still in its early phases」という記述から、終末期の明瞭さが我々に患の脳内で起きていることを理解する手がりを与えていると解釈できます。
  c. 1段落の「Such “terminal lucidity” is defined the return of cognitive faculties」という部分は、終末期の明瞭さが認知能力の突然の回復として明されていることを明示しています。
  d. 2段落の「they’re aware not merely of their surroundings … but understanding what their relationships to other people are」という記述は、終末期の明瞭さが者に予期せぬ形で他人との関係を思いさせることを示しています。

  (5)

  c「A surge of organized brain activity was observed in the last few days of life.」が6段落の実験の記述に言及されていない内容です。本文では、「Gamma-wave activity surged within the first few minutes of cardiac arrest and then ceased」と述べられており、これは心停止の最初の数分間にガンマ波の活動が急増したことを指していますが、最終日の数日間については言及されていません。
  a. 「including a 2013 PNAS study that revealed a similar surge in synchronized brain activity in rats exposed to a cardiac toxin」という部分が、毒素を投与された後の脳活動が観察されたことを示しています。
  b. 「and a 2015 study in which rats were killed by asphyxiation」という部分が、酸素欠乏によって死亡したラットでガンマ波の活動が観察されたことを示しています。
  d. 「Gamma waves are a frequency of brain wave typically associated with wakefulness, alertness and memory recall」という部分が、心停止後の瞬間にラットがより警戒していた可能性を示唆しています。

  (6)

  a「In experiments including both humans and animals, the brain activity of the subjects decreased after a sudden drop in oxygen levels.」は、ジモ・ボルジギンの主張と一致しません。
  8段落で、ボルジギンは「the subjects’ brain showed a spike in activity after the sudden reduction of oxygen supply」と述べており、これは酸素供給の急激な減少後に脳活動が増加したことを意味します。したがって、脳活動が減少したというこの選択肢は、実際には逆の状況を示しています。

  b. 7段落では、「Some other researchers believe this region may also be essential to conscious experience. The parts of the brain in this area are related to visual, auditory and motion perception—a phenomenon Borjigin believes is involved in the out-of-body experiences reported by people who come close to death and recover」と述べられており、頭蓋骨の後ろ近くにある脳の領域が臨死体験に関与していることが示されています。

  c. 7段落の「She adds that gamma-wave activation patterns akin to those observed in the comatose people are associated with activities that include the recognition of a familiar image—such as a human face—in healthy people」という部分が、昏睡状態の患者のガンマ波活動パターンが健康な人が馴染みのある画像を認識する時のそれと似ていることを示しています。

  d. 8段落でボルジギンは、「I believe dementia patients’ terminal lucidity may be due to these kinds of last-ditch efforts of the brain」と述べており、脳が酸素不足を感知したときに生物学的平衡を回復しようとする試みが終末期の明瞭さの原因である可能性があることを示唆しています。

  (8)

  a「Several seconds before cardiac arrest, brain activity was found to disappear.」は、AWARE II研究の記述に適切ではありません。本文には「Within 20 seconds of cardiac arrest, the brain flatlines」とあり、これは心停止の20秒以内に脳の活動がフラットライン（活動が見られなくなる状態）になると述べていますが、心停止の数秒前に脳活動が消失するとは記述されていません。
  したがって、この記述は不適切です。

  b. 「researchers monitored the brain activity of more than 500 critically ill people」という文が、重症患者の脳活動を研究者が監視したことを示しています。
  c. 「The patients were exposed to audiovisual stimuli while undergoing CPR to test their memory of events after cardiac arrest」という文が、心停止後の出来事に関する患者の記憶を探るために、CPR中に視聴覚刺激を受けたことを示しています。
  d. 「The AWARE II team also observed an unexpected spike in brain activity during CPR」という文が、CPR中に予期しない脳活動の急増を研究者が観察したことを示しています。

  (11)

  根拠は3段落にあります。カーロウィッシュは、「what we found is lucidity was more common than it was the exception in dementia patients, which would suggest that the idea of it being terminal is not entirely correct」と述べています。
  さらに、「We’ve actually found that a variety of these episodes occurred months, even years, before the person died」とも述べています。これらの引用は、彼が認知症患者の意識について、完全には失われていないと考えていることを示しており、その意識が部分的には変わらずに存在するという見解を支持しています。

  a「彼らの意識は非常に活発である」、b「彼らの意識は徐々に消えていく」、c「彼らの意識は永久に損なわれる」については、カーロウィッシュの意見を直接反映している引用は文中に見つかりません。彼は認知症患者の意識について、一部が未だに存在し、病気の経験の一部として見るべきであると述べていますが、これらの意識が「非常に活発」であるとか、「徐々に消えていく」とか、「永久に損なわれる」といった具体的な状態を指摘しているわけではありません。

  (12)

  a「questions the idea that cognitive decline is a one-way process」は、記事から合理的に推測できる内容です。11段落でカーロウィシュは、「rather than assuming their consciousness has been irrevocably changed, “we should still pay close attention to their mind because some aspects are still there, though they may be quite damaged.”」と述べており、これは認知機能の衰えが一方通行のプロセスであるという考え方に疑問を投げかけています。彼は認知症の人々の意識が不可逆的に変わってしまったと仮定するのではなく、まだ存在する側面に注意を払うべきだと述べています。

  b. 超自然的な信念や迷信についての言及はなく、科学的な考え方に基づいて死についての見解を述べています。
  c. 新しい技術を開発したという内容は記事には述べられておらず、研究や観察についての言及が主です。
  d. 心臓病の治療への投資を支持するという立場は記事からは直接読み取れません。記事は死の過程や認知症患者の意識についての研究に焦点を当てています。

  出典

  Why Dying People Often Experience a Burst of Lucidity

  2025年早稲田大学教育学部を受ける人はどうするか？

  

  一見すると難しい問題が多いのですが、
  下線問題と空所補充が鍵になるので、教育学部の対策をしっかりと行うことで合格点の点数を取ることは難しくないです。

  絶対に早稲田大学教育学部に合格したい方はお気軽にご相談ください。

早稲田大学人間科学部が2/18に入試を迎えました。 このブログ記事では英語の問題を分析していきます。 ページ目次2024年早稲田人間科学部英語全体講評2024年早稲田人間科学部英語大問I2024年早稲田人間科学部英語大問Ⅱ2024年早稲田人間科学部英語大問Ⅲ2025年早稲田人間科学部を受ける人はどう

• …続きを読む
• 早稲田大学人間科学部が2/18に入試を迎えました。

  このブログ記事では英語の問題を分析していきます。

  2024年早稲田人間科学部英語全体講評

  長文は全体的に紛らわしい問題が多く、昨年度よりも難易度が上がりました。

  また文章の内容についても、相変わらず理系の文章が多くて知識がないとわからないような文章も多くて読みづらいです。

  十分に注意して読む必要があったでしょう。

  解答作成には万全を期していますが、間違えている可能性は十分にありえます。速報ですので、参考程度に留めておいてください。少しですが解説・考え方も載せていますので参考にしてください。
  重要：大学側から配点が公式に発表されてませんので、どれくらいあっていたら合格できるかはわかりません。

  [toc]

  2024年早稲田人間科学部英語大問I

  (1)
  1 C
  2 D
  3 D
  4 D

  (2)
  5 D
  6 A
  7 D

  (3)
  8 B
  9 D
  10A

  (4)
  11 D
  12 D
  13 A

  (5)
  14 C
  15 A
  16 C

  (6)
  17 A
  18 C
  19 C

  (7)
  20 D
  21 D
  22 D

  (8)
  23 B
  24 C
  25 D

  解答根拠

  (I)

  (1)

  選択肢(C)「彼らの降下速度を遅らせるため」が正解です。本文の第2パラグラフにある「Both the wandering salamander and its relative, the arboreal salamander (A. lugubris), often spread their limbs like a skydiver in freefall, maximizing drag. This slowed their descent by as much as 10%, the researchers report today in Current Biology.」という文言がこれを裏付けています。ここで述べられている「maximizing drag」は空気抵抗を最大化することを意味し、「This slowed their descent by as much as 10%」とあることから、彼らが四肢を広げることで降下速度が遅くなることが明示されています。

  選択肢(A)「捕食者から逃れるため」というのも一見正しいように思われますが、本文には「Skydiving could be an effective way to avoid predators.」とあり、これは「スカイダイビングは捕食者を避る効果的な方法である可能性がある」という仮説を示しているに過ぎず、彼らが四肢を広げる主な理由としては直接的に述べられていません。これ第4パラグラフの第1文目です。

  couldを使った助動詞による主観表現と過去形の客観表現を見分けることができるかがポイントです。設問もWhy do なので事実表現を確認しています。

  選択肢B)「より速く降下するため」は、選択肢Cで見た部分の情報と矛盾します。彼らが四肢を広げるこで空気抵抗が増し、実際に降下速度がくなることが明確に述べられているためです。

  選択肢(D)「上記すべての理由」は不適切です。

  (2)

  選択肢(D)「体をくねらせる」が正解です。本文の第2パラグラフには「Other times, the salamanders glided and turned in various directions by wiggling their legs and tail.」とあります。これは、サンショウウオが「legs and tail（脚と尾）」を「wiggling（くねらせる）」ことによって、様々な方向に滑空し、方向転換することを示しており、これが彼らが落下中に方向を変える方法です。

  選択肢(A)「曲げる」、(B)「交差させる」、(C)「伸ばす」という方法については、落下中にサンショウウオが方向を変えるために用いるとは、本文中には記載されていません。したがって、これらの選択肢は不適切です。

  (3)

  本文の第2パラグラフに「Both the wandering salamander and its relative, the arboreal salamander (A. lugubris), often spread their limbs like a skydiver in freefall, maximizing drag.」と述べられており、これは両種が落下中に四肢を広げて空気抵抗を最大化し、落下速度を遅らせるという同様の行動を取ることを示しています。また、「This slowed their descent by as much as 10%, the researchers report today in Current Biology」と続いており、この行動が実際に落下速度を遅らせる効果があることも裏付けています。

  他の選択肢については、本文において直接的に比較されている記述がありません。選択肢(A)「アーボリアルサンショウウオはモントレーエンサティナよりも速く降下できる」、選択肢(B)「モントレーエンサティナはスペックルドブラックサンショウウオよりも落下中のコントロールが劣る」、選択肢(C)「スペックルドブラックサンショウウオはモントレーエンサティナよりも速く木を降りる」という記述は、本文中では見当たりません。

  (4)

  選択肢(D)「情報が不足している」が正解です。本文には、ワンダリングサンショウウオがその名前を得た理由についての直接的な言及はありません。提供された情報は、ワンダリングサンショウウオが高い木に生息し、空中で四肢を広げて降下速度を遅らせる能力についてのみですが、これらの特性が名前の由来に関連しているかどうかは述べられていません。したがって、名称の由来を説明するためには、追加の情報が必要です。

  他の選択肢について検討しますと、選択肢(A)「捕食者を避ける能力」、選択肢(B)「スカイダイバーのように四肢を広げること」、選択肢(C)「登る能力」については、それぞれワンダリングサンショウウオの特徴を述べていますが、これらが名前の由来とされる根拠は文中にはありません。

  出典

  “Watch salamanders ‘skydive’ in a wind tunnel” in Science by ERIK STOKSTAD

  (Ⅱ)

  (5)

  甘い食べ物が若い子供たちに利益をもたらした可能性がある理由は、上記の文章からいくつかの点を引用することで論理的に説明されます。まず、甘い食べ物は「Sugar from fruit or honey was a quick source of complex carbohydrates」と第1パラグラフの3文目で述べられており、複合炭水化物の迅速な源であったことを示しています。これは(a)に関係しています。

  次に、「This preference was once an evolutionary advantage」と第1パラグラフの2文目に記載されており、進化上の利点であったとされています。これは(b)の選択肢の根拠となります。

  最後に、「And fruit that was sweet and ripe gave a person more nutritional value」と第1パラグラフの3文目に述べられており、甘くて熟した果物が人により多くの栄養価を提供したことが明記されています。これは(c)の選択肢の根拠となります。

  上記の引用と説明から、甘い食べ物が若い子供たちにもたらした利益は、複合炭水化物の源、進化上の利点、および栄養価の提供という3つの要素すべてに関連しているため、(d)選択肢「All of the above」が最も適切な答えとなります。

  (6)

  空欄(6)の後And older teens and people in their early twenties discover they no longer care for grape flavored Big League Chew or strawberry Nerds.を考えると、もはや甘いものに対してのpreferenceはないので、下がっているdiminishesと考えられます。
  late adolescence は後期青年期 = older teensという言い換え関係。

  (7)

  味覚の好みが年齢とともに変化する方法について説明する際、選択肢 (a)、(b)、(c) はすべて文章の中に情報を含んでいます。

  (a)については、「We associate different tastes with different consequences」と第2パラグラフの5文目に記述されています。これは、年齢と共に異なる味に対する結果や経験を関連付けて学習するというプロセスを示しており、味覚の好みの変化を説明します。

  (b)に関しては、「A person, for example, might learn that bitter tastes aren’t harmful」と第2パラグラフの6文目,また次の文のThis can prompt a person to try more bitter tastes. で人が苦い味に対する耐性を高める可能性があることを意味します。

  (c)の部分は、先ほどの(b)で引用した同じ文からも根拠を見つけることができます。人々は苦い味が害にならないことを学ぶことができ、これは特定の食品が害を及ぼさないことを学ぶプロセスの一部と言えます。

  出典

  “How Our Sense of Taste Evolves and Adapts” in Discover by　Emilie Le Beau Lucchesi

  Ⅲ

  (8)

  選択肢(a)「全米で初」という記述は、テキストに「first-in-the-nation project」と明記されております（第1パラグラフ3文目）。

  選択肢(b)「世界で初」という記述に関しては、テキストには「first-of-its-kind」という表現が使われており、これはプロジェクトが独自のものであることを示していますが、必ずしも「世界で初」という意味ではないため、この選択肢は誤りです（第1パラグラフ1文目）。また、他の場所で行われている類似の取り組みについての言及もないため、このプロジェクトが世界で初めてであることを裏付ける情報は提供されていません。

  選択肢(c)「初の種類」という表現は、テキストの「first-of-its-kind」という言葉に対応しています（第1パラグラフ1文目）。

  選択肢(d)「どれも誤りでない」という選択肢に関しては、選択肢(b)が不正確であることから、この選択肢も誤りです。

  (9)

  選択肢(a)「いくつかの深刻な水利用の問題を解決する」という記述については、文章ではプロジェクトが「serious water use problems」という問題を修正するとは明言されていません。文章には、「It won’t fix the West’s serious water use problems」との記述があるため、この選択肢は不正確です（第4パラグラフ）。

  選択肢(b)「ソーラーアレイの周囲のスペースを最大限に活用する」という記述に関しては、文章中に明確な言及がないため、このプロジェクトの特異性を表すものではありません。ただし、文章の中で「Figuring out how to maximize space around and under solar arrays is nothing new」と記されており、これはプロジェクトの新規性とは異なる既存のアイデアを指しています（第4パラグラフ1文目）。

  選択肢(c)「気候変動の脅威を解決する」という記述については、文章ではこのプロジェクトが気候変動の脅威を解決するとは述べられておらず、むしろ「the mounting threat climate change poses to water supply」と気候変動が水供給に与える脅威について言及しているため、この選択肢も不正確です（第4パラグラフ、最後の文）。

  選択肢(d)「運河を保護するためにソーラーパネルを使用する」という記述は、文章中で「constructing solar panels as a protection measure for irrigation canals is a new idea」と述べられています（第4パラグラフ、3文目）。これは、ソーラーパネルを使って運河を覆い、水の蒸発を防ぐというプロジェクトの独特な側面を指しており、この選択肢はプロジェクトのユニークな特徴を正確に表しています。

  (10)

  選択肢(a)「パネルが水の汚染を防ぐ」という記述については、文章中では水質汚染の防止について言及されていません。このプロジェクトが水質汚染を防止するという情報は提供されていないため、この記述は水とソーラーパネルがどのように連携するかを説明していないと言えます。

  選択肢(b)「ソーラーパネルが蒸発を減少させる」という記述は、テキストに「Covering all the canals in the state with solar panels … could save 63 billion gallons of water annually」とあるため、これは水の蒸発を減らすことを示しています（第3パラグラフ2文目）。従って、この選択肢は水とソーラーパネルの連携を正確に説明しています。

  選択肢(c)「水路がソーラーパネルを冷却するのに役つ」という記述もまた、テキストに「The water’s cooling effect in turn, could help keep those solar panels working more effectively」と記載されているため、正確な記述です（第3パラグラフ、最後の文）。

  出典

  “How installing solar canopies over canals can help California fight drought” in The Hill

  Ⅳ

  (11)

  “choose”：選択肢の中から選ぶという一般的な行動を示しており、フォーマルでもカジュアルでも使用できます。
  “agree”：提案されたことや条件に対して同意することを意味し、他者からの提案に対する反応として使われることが多いです。
  “elect”：選択肢の中から意識的に選ぶことを意味し、しばしば公式な文脈や選挙などの文脈で使われます。

  (12)

  ECoG（脳皮質電極記録）プロセスが人間に対して稀にしか使用されない理由は、その侵襲性の高さにあります。本文の第2パラグラフにおいて、「Electrocorticography is not typically performed in humans because of its invasiveness」と明記されています。
  これは、ECoGプロセスが侵襲的であるため、通常は人間に対して行われないことを意味しています。

  a)「Can induce epileptic seizures」、(b)「Expensive to conduct」、及び(c)「Requires brain surgery」のいずれも、本文中に「Electrocorticography is not typically performed in humans because of its invasiveness」と直接関連する情報は含まれていません。

  (13)

  この記事の主なアイディアは、特定の脳の部分が歌声によって活性化されるという発見です。従って、選択肢(a)「One part of the brain activated by singing」が正しい答えです。本文の第1パラグラフの最初の文、「Researchers from the Massachusetts Institute of Technology have discovered that a specific set of neurons located in the auditory cortex in the brain respond to singing but not other sounds like speaking or instrumental music」と述べています。これは、聴覚皮質に位置する特定のニューロン群が歌声に反応することを示しており、本文の主要なアイディアをしています。

  選択肢(b)「Researchers find a brain function anomaly」については、記事では脳機能の異常が発見されたとは述べられていませんので、不適切です。選択肢(c)「Scientists study how the brain processes sounds」はこの研究の一部を表していますが、記事の主なアイディアではありません。選択肢(d)「The challenges of studying neural responses」についても、本文では研究の挑戦についての詳細は述べられておらず、主なアイディアとは言えません。

  出典

  “Some Neurons in Your Brain Respond to Singing but Not Other Music”in Smithsonian Magazine

  Ⅴ

  (14)

  最も深刻な脱水の副作用は(c)Stroke、つまり脳卒中です。この情報は本文の第1パラグラフの最後の文、「Dehydration comes with a slew of nasty side effects like mental fog, overeating and even higher stroke risk.」に基づいています。ここで言及されている「higher stroke risk」というフレーズは、脳卒中のリスクが他の副作用よりも特に深刻な健康問題を示唆しています。したがって、脱水が引き起こす可能性のある最も重篤な副作用として脳卒中が挙げられます。

  他の選択肢に関してですが、(a)Mental fogと(b)Overeatingは確かに脱水による副作用ですが、本文ではこれらが最も深刻であるとは述べられていません。これらの表現も第1パラグラフにありますが、脳卒中のリスクが特に強調されているため、これらは(c)Strokeに次ぐ副作用と考えられます。

  最後に(d)Not enough information givenについては、上記の理由により不適切です。なぜなら脳卒中が最も深刻な副作用であるという情報は文中に明記されているため、情報が不足しているわけではありません。

  (15)

  選択肢の中で、脱水に役立たない可能性があるのは(a)Coffeeです。
  本文には、最も良い水分補給方法として、水分を多く含んだ食品を摂ることが推奨されています。第2パラグラフに「hydrating foods like watermelon, tomatoes and beans (most raw fruits and vegetables have a high water content)」とあり、これには(b)Raw fruits、つまり生の果物と(d)Tomatoes、が含まれています。これらは水分補給に役立つとされています。

  また、(c)Tea、つまりお茶も水分補給に有効であると本文の第2パラグラフ最終文に記述されています。「They found that milk, tea and orange juice were slightly more hydrating than water alone」との記載があります。したがって、お茶は水分補給に役立つ飲料の一つです。

  (16)

  脱水を避ける最善の方法は(c)Have a mix of hydrating foods and water、つまり水分を多く含む食品と水を組み合わせることです。本文の第2パラグラフにおいて、水分を多く含む食品として「watermelon, tomatoes and beans (most raw fruits and vegetables have a high water content)」が挙げられており、これらの摂取が推奨されています。また、第2パラグラフ最後から２文目では「other drinks might be more hydrating than water alone」とあり、水だけではなく他の飲料も水分補給に有効であることが述べられています。
  これらの情報は、水分補給には水だけでなく、水分を含む食品や他の飲料も取り入れることが重要であることを示しています。

  他の選択肢についてですが、(a)Avoid high-intensity exercise、つまり高強度の運動を避けることが脱水を防ぐ方法として本文には述べられていません。
  そして(b)Drink lots of water、つまり多くの水を飲むことは脱水を避ける一つの方法ですが、本文では「Chugging as much water as you can all day is likely not the best or most efficient way to stay hydrated」と述べられており、一日中大量の水を飲むことが最も効率的な方法ではないと指摘されています。

  最後に(d)Reduce alcoholic drinksについては2パラグラフ最後のwhile beer was slightly (but not significantly) less hydrating.にてhydrateとは逆のことが書いてあります。

  出典

  Why Drinking Water All Day Long Is Not the Best Way to Stay Hydrated

  Ⅵ

  (17)

  3パラグラフ2文目に「“What they define as an ‘optimal’ diet is not quite optimal; it’s just a whole lot better than typical,’” Katz said」とあります。これは、彼が研究で提案されている事を「最適」とは考えていないが、「典型的なものよりはるかに良い」としていることを示しています。
  その後の文章でも、彼はその食事をさらに改善することで、さらなる利益をもたらす可能性があると感じており、「much improved（大幅に改善された）」食事であっても、まだ相当量の肉と乳製品を許容していると指摘しています。したがって、選択肢の中でDr. Katzの見解に最も適合するのは(a) Betterです。

  (b) Considerable この単語はKatzが食事について述べたの評価としては使用されていません。
  (c) Optimal: これはKatzが研究で定された食事に対して使用している言葉ではなく、彼は「optimal」という言葉を使って食事を否定的評価しています（「”optimal” diet is not quite optimal」と述ています）。
  (d) Typical: Katzは研究で提案されてる食事を「typical（典型的な西洋食）」よも優れていると評価しており、したがってこの選択肢も彼の見解とは異なります。

  (18)

  本文2パラグラフ、2文目には「A man eating the healthier diet from age 20 could add 13 years to his life.（20歳から健康的な食事を始めた男性は、彼の寿命に13年を加えることができる）」とあります。これは、この最適化された食事を最も早く始める若い男性が最も多くの寿命の延長を見込むことができることを示しています。。したがって、選択肢の中では(c) Younger menが最も恩恵を受けるグループとして選ばれるべきです。

  (a) 80-year-olds: 彼らも恩恵を受けることができますが、本文によるとその増加は約3.5年とされており、他のグループと比べると恩恵が少ないです。
  (b) Older women: 彼らも寿命を延ばすことができますが、60歳から始めた場合の増加は8年であり、若い男性と比べると少ないです。
  (d) Younger women: 20歳の若い女性も寿命を大きく延ばすことができますが、その増加は10年以上であり、若い男性の13年よりは少ないです

  (19)

  提案されている「最適化された食事」においては、肉や加工食品よりも植物ベースの食品に焦点を当て、肉や加工食品を減らし、果物、野菜、豆類、全粒穀物、ナッツに置き換えることが推奨されています。しかし、提案された食事内容には「肉を魚に置き換える」という具体的な記述はありません。したがって、選択肢の中で行わないことは(c) Replace meat with fish, vegetables, legumes, grains and nutsです。

  (a) Focus on plant-based foods over meat and processed foods: これは、最適化された食事の一部として明示されています。本文の1つ目のパラグラフ、2文目で「less red and processed meat and more fruits and vegetables, legumes, whole grains, and nuts」と記述されており、植物ベースの食品に焦点を当てることが提案されています。

  (b) Increase plant-based foods, decrease meat and processed foods:これも本文の1つ目のパラグラフ、2文目の記述に基づいて、最適化された食事の特徴として挙げられています。

  (d) Shift emphasis from red meat to fruits and vegetables: 1つ目のパラグラフ2文目「less red and processed meat and more fruits and vegetables」とあることから、赤肉から果物や野菜への重点シフトも提案された食事の要素であることがわかります。

  出典

  Changing your diet could add up to 13 years to your life, study says

  Ⅶ

  (20)

  Aviation Englishの目的として挙げられていないものを選ぶ問題です。まず、各選択肢を検討しましょう。

  (a)「誤解を避ける」: Aviation Englishは、パイロットと航空交通管制官との間の誤解を避けるために、標準的なフレーズを使用します。これは文の中で、「Because a misunderstanding between a pilot and a controller can lead to catastrophe, aviation English relies upon a standard phraseology」と第3パラグラフの2文目で述べられています。

  (b)「コミュニケーションを促進する」: Aviation Englishは、国際的なフライトでは特殊なバージョンの言語として利用され、パイロットと航空交通管制官が無線でコミュニケーションを取る際に使用されます。これは、第1パラグラフの最後の文、「pilots on international flights and air traffic controllers on their routes are required to speak a specialized version of the language known as aviation English when they communicate over the radio」と記載されており、コミュニケーションを促進するためのものであることがわかります。

  (c)「安全を促進する」: 航空英語の主な目的の一つは安全を促進することです。これは、誤解が「災害につながる可能性がある」と第3パラグラフの2文目で述べられており、安全性の確保が重要であことが示されています。

  (d)「時間を節約する」: この選択肢に関しては、文章中時間の節約について直接的に言及されている部分はされてません。Aviation Englishの複雑さとニュアンス多さが強調されており（第3パラグラフ時間の節約よりは誤解を避け、明確なコミニケーションを図ることが目的とされています。

  以上の分析に基づき、(d)「時間を節約する」がAviation Englishの目的として挙げられていないものです。

  (21)

  (a)「複雑（Complex）」: Aviation Englishは、「in some ways it’s much more complex and nuanced」と第3パラグラフで述べられています。これは、言語が持つ独特の複雑さや微妙なニュアンスを指摘しており、そのため、Aviation Englishは複雑であると言えます。

  (b)「国際的（International）」: Aviation Englishは「pilots on international flights and air traffic controllers on their routes are required to speak a specialized version of the language」と第1パラグラフの最後の文で述べられており、国際的な航空フライトおよび航空交通管制における標準言語として機能していることがわかります。これにより、Aviation Englishは国際的な特性を持っています。

  (c)「実用的（Practical）」: Aviation Englishの使用は、実際のパイロットと航空交通管制官間のコミュニケーションにおいて非常に実用的です。これは、「a prescribed, highly constrained set of phrases to be used insofar as possible」と第4パラグラフの2文目で定義されており、実際の飛行オペレーションにおける明確性と理解のための実用的な言語であることを示しています。

  (d)「すべての上記（All of the above）」: 上記の(a)、(b)、(c)の各説明から、Aviation Englishが複雑であり、国際的であり、実用的であることが示されているため、最も適切な選択肢は(d)「すべての上記」です。

  (22)

  (a)「Aviation English Helps Passengers Communicate with Flight Crew」: この選択肢は不適切です。本文は、乗客とフライトクルー間のコミュニケーションに焦点を当てていません。むしろ、パイロットと航空交通管制官間のコミュニケーションについて述べています。第1パラグラフには、「pilots on international flights and air traffic controllers on their routes are required to speak a specialized version of the language known as aviation English when they communicate over the radio」とあり、乗客ではなくパイロットと管制官のやり取りについて説明しています。

  (b)「How Simplified Morse Code Changed the Safety of Air Travel」: この選択肢も不適切です。本文は、モールス信号の簡略化が航空の安全にどのように影響を与えたかについて詳述しているわけではありません。第2パラグラフでは、初期の航空通信にモールス信号が使われていたことと、その後の発展について簡単に触れていますが、これがタイトルとして本文全体を代表するものではありません。

  (c)「International Language Promotes Intercultural Communication」: この選択肢も本文の主題を正確には反映していません。確かに航空英語が国際的な言語であることは第1パラグラフに記載されていますが、この言語が異文化間コミュニケーションを促進するというよりは、特定の専門的なコンテキスト、つまり航空交通の安全性を高めるために用いられています。

  (d)「Pilots use Universal Language to Enhance Flight Safety」: この選択肢が本文の内容を最も適切に表しています。本文は、航空英語がいかにして国際的な航空通信の標準として確立されたか、そしてそれがパイロットと航空交通管制官間の明確なコミュニケーションを通じて飛行の安全性をいかに向上させるかに焦点を当てています。第4パラグラフにある「Because a misunderstanding between a pilot and a controller can lead to catastrophe, aviation English relies upon a standard phraseology」という文言が、このタイトルの妥当性を裏付けています。

  出典

  ‘Tree-niner-fife’: The Global Language of Pilots

  Ⅷ

  (23)

  ヒエログリフ（象形文字）が最初にどのように使用されたかについて言及している部分は、3番目のパラグラフの1文目にあります。「Archaeologists have taught us that before the alphabet was invented, “written” communication was in the form of pictures, known as hieroglyphics. They are believed to have originated around 3100 BCE., not as a way to capture history, but as a method for documenting business transactions during the rise of the city-state.」この文は、象形文字が歴史を記録するためではなく、都市国家の台頭中にビジネス取引を文書化する方法として起源を持っていると説明しています。従って、選択肢 (a) Capture history や (c) Record news はこの文に基づいて否定されます。

  また、選択肢 (d) All of the above についても否定されるべきです。なぜなら、文書にはヒエログリフがビジネス取引の文書化以外に使われたという言及がなく、選択肢 (a) や (c) の内容が含まれていないためです。

  したがって、正しい答えは (b) Document business であり、これが象形文字が最初にどのように使用されたかについての文書からの引用に基づいた論理的な説明です。

  (24)

  4パラグラフの最後の文に、「While it’s not clear exactly when or how, researchers say sometime in the second millennium — between 1900 and 1700 BCE — an alphabetic system was developed that enabled more people to read and write.」とあります。これは、紀元前1900年から1700年の間の第二千年紀に、より多くの人が読み書きできるようにするアルファベットシステムが開発されたことを示しています。

  選択肢 (a) Easier to communicate at a distance については、文章中で直接的な言及がないため、これを根拠とすることはできません。選択肢 (b) History could be more easily recorded も、直接的な言及がないため、根拠とはなりません。選択肢 (d) Scribes were no longer panda については、文章中にスクライブ（筆記者）が「パンダ」でなくなったという記述はどこにも存在せず、また「パンダ」という言葉は文脈上無関係なため否定されます。

  (25)

  最後のパラグラフで、イービング・フィンクルはアルファベットシステムへの移行を記述しており、「The giant leap came when somebody conceived of this matter, that you could draw a picture which represented something that someone could recognize but at the same time that sign could be used just for the sound of the thing it looked like, so the sound became drawn out or separated from the picture」と述べています。これは、象形文字からアルファベットシステムへの移行が「giant leap」と表現されていることを示しています。

  また、同じ文でこの移行が「rather simple」とも述べられており、これは選択肢 (a) Conceptually simple の根拠になります。さらに、最後の部分には「nevertheless is of great lasting significance」とあり、これは選択肢 (c) Significant の根拠となります。

  したがって、文中の引用に基づき、選択肢 (a) Conceptually simple、(b) Giant leap、(c) Significant はすべてこの移行を説明するのに適切な形容詞であり、それぞれの言葉が文章の中で直接的に使われているため、正解は (d) All of the above となります。

  出典

  Why Was the Alphabet Invented, Anyway?

  2024年早稲田人間科学部英語大問Ⅱ

  26,G of
  27,J to
  28,G of
  29, I out
  30,F in
  31,J to
  32,L No WORD
  33,D for
  34,B about
  35,I out
  36,C by
  37,E from
  38,A at
  39,K up
  40,A at

  2024年早稲田人間科学部英語大問Ⅲ

  41,B
  42,C
  43,B
  44,A
  45,E
  46,A
  47,C
  48,B
  49,E
  50,D

  解答根拠

  41,文中の “it is no point in” は文法的に正しくありません。正しくは “there is no point in” となるべきです。”It is no point” では主語と述語が不適切に使われています。
  42, “much troubles” は不正確です。不可算名詞の “trouble” を使うべきで、”much trouble” が正しい形です。
  43,”for aged” は不適切な表現です。 “for the aged” または “for elderly” が正しい表現です。
  44,”so please” は誤りです。 “so pleased” が正しい形容詞の使用です。
  45,No Error
  46,”I find” は現在形が不適切であり、過去形の “I found” が正しい可能性があります。
  47,”some of whose” は不正確です。正しくは “some of which” となります。
  48,”equipments” という単語は誤りです。”Equipment” は不可算名詞であり、複数形は存在しません。
  49,No Error
  50,”sun raise” は誤りで、正しくは “sunrise” または “sun rise” となります。

  2025年早稲田人間科学部を受ける人はどうするか？

  

  来年度より人間科学部は受験方式が変わりますが、英語については同じ傾向が続くと考えられます。

  主観、客観表現を正確に読み分けられるのと、文章を照らし合わせていく力が必要です。

  早稲田大学人間科学部で合格するためには人間科学部に合格するための読み方、解き方が必要です。

  お気軽にご相談ください。

早稲田大学法学部が2/15に入試を迎えました。 このブログ記事では英語の問題を分析していきます。 2024年早稲田法学部英語全体講評 大問1の長文が読みづらいのと(3)が新形式で解きづらかったと思います。 新形式の問題は後で落ち着いて見れば、できても当日の緊張感で解くのはかなり大変だったと思います。

• …続きを読む
• 早稲田大学法学部が2/15に入試を迎えました。

  このブログ記事では英語の問題を分析していきます。

  2024年早稲田法学部英語全体講評

  大問1の長文が読みづらいのと(3)が新形式で解きづらかったと思います。
  新形式の問題は後で落ち着いて見れば、できても当日の緊張感で解くのはかなり大変だったと思います。
  そもそも日本史選択は何の話をしているのかわからなかった生徒もいたかもしれません。
  ＊早稲田法学部は過去にも歴史上の出来事の問題を出題しています。

  また、大問2はここ数年出題されてなかったパラグラフ形式が復活しましたね。
  「今年はでない！」と思って鷹を括っていた人は急に出てきて辛かったかもしれません。

  作文については例年通りなので、長文で点数をいかにつけられなかったかが勝負となっています。

  2024年早稲田法学部英語大問1

  (1)
  1A
  2C
  3D
  4A
  (2)
  1,C
  2,B
  3,D
  4,B
  (3)
  1,D
  2,D
  3,B
  (4)
  1B
  2A
  3B
  4C

  解答根拠

  (1) 1

  A. 「特別な政府のコインを使用して支払うことができた」
  これについての直接的な言及はありませんが、「a token like the one above」という記述は第2パラグラフにあります。しかし、これは「政府のコイン」という意味ではなく、ひげ税を支払った証としてのトークンに関するものです。

  B. 「ツァーリの日常生活への浸透の程度を示している」
  「His inspectors stalked the streets of St. Petersburg, shaving beards and snipping inches off coats.」という記述は第1パラグラフにあり、ツァーリの影響が日常生活に及んでいたことを示しています。

  C. 「政治権力の行使についての疑問を提起している」
  この選択肢については直接的な引用はありませんが、政治権力の行使とその影響に関する全体的な議論は、本文全体を通じて存在します。

  D. 「人の地位に応じて異なる税率で徴収された」
  「a few kopecks for peasants, a hundred rubles or more for nobles or military officials」という記述は第2パラグラフにあり、税率が地位によって異なっていたことを明示しています。

  E. 「ロシアの文化変革を加速するために設計された」
  「The beard tax was just one part of a larger project: Peter the Great’s aesthetic reinvention of Russian culture.」という記述は第3パラグラフにあり、ひげ税が文化変革の一環であったことを示しています。

  (1) 2

  A. 「外交的な呼びかけと華やかな社交集会を含んでいた」
  これについては第4パラグラフに「He visited heads of state, collections of natural curiosities, and anatomical theaters, and threw legendarily wild parties.」という記述があります。これは外交的な訪問と豪華な社交イベントを含んでいたことを示しています。

  B. 「その土地についての好奇心旺盛な訪問者についての誇張が触発された」
  これに関しては第4パラグラフに「excited rumors of his visit spread from town to town, heralding him as a giant: 7 feet tall, brilliant, and only half-civilized.」とあることから、ピョートルの訪問についての誇張された噂が広まったことがわかります。

  C. 「新しいロシアのツァーリの戴冠を祝うことを目的としていた」
  この選択肢に関連する記述は文中には存在しません。ピョートルの1697年のツアーは、新しいツァーリの戴冠を祝う目的ではなく、外国の知識を得るためのものでした。

  D. 「ピョートルに外国についての直接的な知識を得させた」
  第4パラグラフには「For a time, he worked at a Dutch shipyard to learn ship-building techniques.」とあり、ピョートルが直接的に外国で知識を得たことが示されています。

  E. 「物議を醸すロシアの文化政策の結果となった」
  第5パラグラフに「Upon returning from his travels, he launched immediately into the process of “Europeanizing” his homeland.」とあります。これは彼の旅行がロシアの文化政策に影響を及ぼしたことを示しています。

  (1) 3

  A. 「服装や身だしなみのような日常的な慣習にまで及んだ」
  これについては第3パラグラフにある「The tsar ordered his subjects to replace their familiar long Russian overcoats with French or Hungarian jackets.」や「His inspectors stalked the streets of St. Petersburg, shaving beards and snipping inches off coats.」という記述が、日常的な慣習にも及んだことを示しています。

  B. 「既存の美的規範の全面的な見直しを意味した」
  これについては第3パラグラフに「Peter the Great’s aesthetic reinvention of Russian culture.」という記述があり、美的規範の見直しを意味していたことが示されています。

  C. 「ロシアの確立された構造に挑戦をもたらした」
  これについては第1パラグラフと第2パラグラフにある、ひげ税の導入や服装の変更要求が既存の構造への挑戦を示しています。

  D. 「改革の犠牲として彼の個人的な嗜好を促進した」
  この選択肢に関しては、文中にピョートル大帝が個人的な嗜好を推し進めた結果として改革が犠牲になったという記述はありません。改革は彼の欧州旅行の経験に基づいており、個人的な趣味趣向を反映するものではなく、より広範な「Europeanization」プログラムの一環でした。

  E. 「一部のロシア人にとって不快なものであった」
  これに関しては第3パラグラフにある「anyone walking the streets in an old-fashioned robe was liable to have it shorn short by the Tsar’s inspectors.」や最後のパラグラフにある「The implicit choice was clear: Peter or the Church.」という記述が、一部のロシア人がプログラムに対して不快感を持ったことを示唆しています。

  (1) 4

  A. 「ピョートルの統治をスキャンダルを避ける限り受け入れた」
  この選択肢に関しては文中にはロシア正教会がピョートルの統治を受け入れたかどうかについての明確な記述はありません。ただし、文中には教会が彼のいくつかの行動について否定的な意見を持っていたことが示唆されていますが、「スキャンダルを避ける限り」という条件については言及されていません。

  B. 「ピョートル大帝の近代化努力によって脅かされたと感じた」
  第4パラグラフには「The beard tax was just one way that the Tsar sparred with the Church.」という記述があり、ピョートル大帝の政策が教会との対立を示しています。

  C. 「信者に対して宗教的な理由からひげを価値あるものと教えた」
  第7パラグラフに「the teachings of the Russian Orthodox Church, which considered uncut facial hair a reflection of piety.」とあり、教会がひげを宗教的な理由で価値あるものと教えていたことが示されています。

  D. 「ひげ税をロシアの宗教生活への乱れと見なした」
  第8パラグラフには「To the pious, the beard tax was a shocking scandal.」とあり、ひげ税が信心深い人々にとっては大きな問題であったことが示されています。

  E. 「アストラハンの反乱兵によって守られた」
  第8パラグラフには「Finally, in 1705, the Russian military division initiated an open revolt in the town of Astrakhan. A letter from the rebels proclaimed that they were taking a stand for the Christian faith, and against shaving and foreign dress.」とあり、反乱兵が宗教的な理由でピョートル大帝の政策に反対したことが示されています。

  (3) 1

  引用文は、ピョートル大帝の政策に反対した人々の立場を表しているようです。それぞれの選択肢を検討してみましょう。

  A. キャプテン・ジョン・ペリー（Captain John Perry）
  キャプテン・ジョン・ペリーは文中で引用されていますが、彼は訪問者としての視点で情報を提供しており、この引用は彼の立場を代表するものではありません。

  B. サンクト・ニコラス（Saint Nicholas）
  サンクト・ニコラスはロシア正教会の聖人であり、彼による引用とは考えにくいです。

  C. 全てを笑い飛ばすものと酔っ払いの宗教的集会（the All-Jesting and All-Drunken Religious Assembly）
  この集団は、ピョートル大帝によって創設されたものであり、彼の政策を支持するために存在したものです。この引用が彼らに帰属する可能性は非常に低いです。

  D. アストラハンで反乱を起こした兵士たち（the soldiers who revolted in Astrakhan）
  第8パラグラフで、「Finally, in 1705, the Russian military division initiated an open revolt in the town of Astrakhan. A letter from the rebels proclaimed that they were taking a stand for the Christian faith, and against shaving and foreign dress.」とあります。これは反乱を起こした兵士たちがキリスト教の信仰を守り、剃毛や外国の服装に対して立ち上がったことを示しています。この引用はその立場を反映しているため、最も可能性が高いです。

  E. V.M.ジヴォフ（V. M. Zhivov）
  V.M.ジヴォフは「Cultural Reforms in Peter I’s System of Transformations」という論文の著者であり、彼の立場から引用されたものではないでしょう。

  (3)2

  文章に基づいて、ピョートル大帝が「見せて教える」方法を用いて、彼の政策に関する無知を理由に公衆が自らを免罪することを防いだ例を挙げる問題ですね。

  A. ピョートルが秘密裏にヨーロッパを訪れた方法
  第4パラグラフに「In 1697, when he set out on a grand tour, Peter chose to travel incognito, adopting the name “Sergeant Pyotr Mikhaylov.”」とありますが、これは公衆に彼の政策を知らせるための手法とは関連していません。

  B. ツァーリが主催した伝説的に野放図なパーティー
  これについては第4パラグラフに記述がありますが、「見せて教える」手法とは直接的な関連が見られません。

  C. 大工にひげを保持させたこと
  第6パラグラフには大工の話がありますが、彼のひげを保持させるという行為は、政策への理解を促進するための「見せて教える」方法とは異なります。

  D. モスクワ市の門の外に設置されたマネキン
  第3パラグラフに「Mannequins set outside the Moscow city gates illustrated the new fashions for all to see.」とあります。これは、新しい服装の方針を公衆が見て理解することを可能にするための、まさに「見せて教える」手法の一例です。

  E. 偽の宗教的儀式とセレモニー
  9パラグラフには、ピョートル大帝が宗教的な集会を行ったことが記述されていますが、これは彼の政策を知らせるためではなく、忠誠のテストとしての要素が強いです。

  (3)3

  この質問における文脈から推測すると、ツァーリの不在中に彼の高官の妻たちが古風なガウンを教会で着用していたこと、そしてそれを隠すためにスカートを重ね着していたことが示されています。彼女たちがツァーリの命令を呪いながらこれを行っていたことから、そのスカートは何らかの反抗の意を表していた可能性があります。

  A. ヨーロッパ風のスタイル。
  B. 抗議の意味を持っていた。
  C. エリートの印。
  D. 伝統的なロシア式。
  E. 誇りを持って着用されていた。

  文中には「everyone wore German dress」とあるので、ツァーリの政策に従ってヨーロッパ風のドレスを着ていたことが示されています。しかし、この文はまた、「the wives of some of the Tsar’s leading officials wore old-fashioned gowns to church」とも述べており、これは彼女たちが伝統的なロシアの服装を身につけていたことを示しています。さらに、「even though they put skirts over them」とあるので、彼女たちがそれらの古風なガウンを隠すためにスカートを重ね着していたことがわかります。

  この情報から推測するに、スカートは伝統的なロシア式のガウンを隠すために用いられたものであり、ツァーリの命令に反対していたことを示唆しているため、Bが答えとなります。

  出典

  Amelica Soth “Peter The Great’s Beard Tax” JSTOR Daily

  2024年早稲田法学部英語大問2

  (1)
  1 C
  2 K
  3 H
  4 I
  5 J
  6 G
  7 D

  (2)
  1 E
  2 A
  3 D
  4 D

  (3)
  1D
  2C
  3A

  (4)
  1B
  2C
  3E

  出典

  Thomas A DiPrete and Claudia Buchman, The Rise of Women

  解答の根拠

  (1) 第1段落

  第1段落では、20世紀の初めから女の子が男の子を学業成績で上回っていたという歴史的証拠を概説しています。「Even then, girls earned higher grades than boys and were promoted to the next year level more readily.」という部分で、女の子がより高い成績を得て、より容易に次の学年に進級したことが示されています。

  (1) 第2段落

  第2段落では、19世紀の大部分にわたり若い女性が大学への入学が禁じられていたこと、そして女性の大学への入学が初めて許可されたのが1837年であること、南北戦争が女性の大学入学者数増加にどのように影響したかについて詳述しています。「By 1900, more than twice as many women were enrolled in coeducational institutions as were enrolled in women’s colleges.」という部分で、共学の大学に入学する女性の数が女子大に入学する女性の数の2倍以上になったことが示されています。

  (1) 第3段落

  第3段落では、幼稚園から大学に至るまで、全主要科目で女の子が男の子よりも良い成績を取っていること、そしてこのことが男の子の教育成績をどのように改善できるかについての疑問を提起しています。「From kindergarten through high school and into college, girls get better grades than boys in all major subjects, including math and science.」と記述されています。また、選択肢のleading to の部分は本文のThis leads us to ask if school-based policies can help improve the educational performance of boys.に 一致。

  (1) 第4段落

  第4段落では、教師、学生文化、および教授法と評価技術に焦点を当てた学校政策の介入が学生の成果を改善する可能性がある三つの主要な領域について説明しています。「Three promising arenas of school policy intervention have the potential to improve student outcomes: teachers, student culture, and instructional and evaluation techniques.」という部分でこれらの領域が概説されています。

  (1) 第5段落

  第5段落では、学業成績を軽蔑する一般的な認識に反して、学生が実際には学業成績を価値あるものと見なしていることが示されています。「…students do not generally disparage academic achievement, so long as it is accompanied by other desirable behaviors…」という部分で、学業成績に対する学生の肯定的な態度が強調されています。

  (1) 第6段落

  第6段落では、8年生の生徒がどの程度成績を重視しているか、また彼らが自分の親が成績をどれほど重視していると認識しているかについての調査結果が紹介されています。「Eighth-grade students were asked how important grades were to them and how important they perceived grades to be to their parents.」という部分で、教育価値観に関する生徒の認識が説明されています。

  (1) 第7段落

  第7段落では、女性が教育成果で優位に立つ現象が現れた今、学校の政策がどのように性別不平等に影響を与えるか、そして男女両方に役立つ政策が必要であるかについて検討しています。「Now that a female advantage in educational achievement has emerged, it is natural to ask whether and how schools affect gender inequality.」という部分で、性別に基づく不平等に対処するための学校政策の必要性が強調されています

  (2) 1

  本文では女の子が幼稚園から高校、さらに大学に至るまで、全ての主要科目で男の子よりも良い成績を取っていると述べられています。

  3段落目で、「As early as kindergarten, girls demonstrate more advanced reading skills than boys, and boys continue to have problems with reading in elementary school. From kindergarten through high school and into college, girls get better grades than boys in all major subjects, including math and science.」と記載されています。この引用は、女の子が幼稚園でより進んだ読解能力を示し、その後も小学校を通じて、そして高校や大学に至るまで全ての主要科目で男の子よりも良い成績を取ることを明確にしています。
  この情報に基づき、E選択肢がパッセージと矛盾する唯一の選択肢であることがわかります。女の子が「幼稚園を卒業するまで」より進んだ読解能力を示すという記述は、女の子が幼稚園から先も、学業全般において男の子より優れているという本文の情報と合致しません。

  (2) 2

  B本文の2段落目で述べられています: 「They were first allowed to enroll in college in 1837, when Oberlin College began admitting women, arguably to provide ministers of religion with intelligent, cultivated, and thoroughly schooled wives.」これは、女性が最初に大学に入学した理由が、結婚のために教育されることが主な目的であったことを示唆しています。

  C、2段落目で「…the rapid rise in the number of women enrolling in coeducational institutions precipitated a new fear that women would take over colleges.」と述べられており、1900年代に女性の大学への入学者数が急速に増加し、大学を乗っ取るのではないかという懸念が生じたことを示しています。

  D、同じく2段落目で触れられています: 「When the Civil War (1861-1865) led to a shortage of male students, more colleges became willing to enroll tuition-paying female students.」これは、南北戦争中に男子学生が減少したことで、より多くの大学が女子学生の入学を奨励したことを示しています。

  E2段落目の冒頭で確認できます: 「They were first allowed to enroll in college in 1837…」とあり、女性が初めて大学への入学を許可されたのが1837年であることを明らかにしています。

  これらの引用を基に、A選択肢「1900年までに、女性の大学への入学者数が、大学に入学している男性の2倍になった。」が本文と矛盾していることがわかります。本文では、「By 1900, more than twice as many women were enrolled in coeducational institutions as were enrolled in women’s colleges.」と記述されており、これは共学の大学に入学している女性の数が、女子大に入学している女性の数の2倍以上になったことを意味していて、女性の入学者数が男性のそれの2倍になったとは述べていません。したがって、Aが本文の内容と合致しません。

  (2)3

  A、4段落に記載: 「…and academically oriented student cultures may improve both the effectiveness of some teachers and the impact of some instructional techniques.」これは、学問的に志向された学生文化の創造が、一部の教師の効果といくつかの教授技法の影響を改善する可能性があることを示しています。

  Bについては、同じく4段落目で言及されています: 「Considerable research suggests that small class sizes are better than large ones…」とあり、小規模クラスが大規模クラスよりも優れていることを示唆する多くの研究があることを示しています。

  Cもまた、4段落目で言及されています: 「Beyond teachers, other support staff such as guidance counselors may play an important role in students’ educational outcomes.」これは、ガイダンスカウンセラーなどのサポートスタッフが、学生の教育成果に重要な役割を果たす可能性があることを示しています。

  Eについては、4段落目で述べられています: 「…good teachers have long-lasting effects on their students.」および「…teachers differ in their ability to promote these skills.」これは、高品質の教師が学生に長期的な影響を与え、社会的および行動的スキルの促進において教師による差があることを示しています。

  これらの引用を基に、D「raising academic standards to improve overall academic performance.」が本文の内容と矛盾していることがわかります。本文の4段落目で、学術基準を引き上げることが全体的な学術成績を向上させるわけではないと述べられています: 「…that putting students into college preparation tracks is generally detrimental to poorly performing students, and that tough academic standards do not boost academic achievement for poorly performing students.」これは、成績が悪い学生にとっては、学生を大学準備コースに配置することが一般的に有害であり、厳しい学術基準が成績が悪い学生の学業成績を向上させないことを示しています。したがって、Dが本文と合致しない選択肢です。

  (2)4

  5段落目で、John Bishop と彼の同僚による中学生と高校生に対する調査結果が紹介されています。

  Aは5段落目で言及されており、「Apparently students begin to cross the “not cool” line when they exhibit overt competitiveness about grades (51 percent said this is not cool, but still 49 percent disagreed)…」と記述されています。これは約半数の生徒が成績について公然と競争的であることを受け入れていることを示しています。

  Bもまた言及されています。「…73 percent disagreed with the statement that “it’s not cool to be enthusiastic about what you are learning in school.”」とあるため、約四分の三が学校で学んでいることに熱心であることを良いと考えています。

  C選択肢は、「…students generally appreciate that high levels of educational achievement are valuable in today’s world.」と記載されていることから、大半の生徒が教育成果の価値を認識していることを示しています。

  E選択肢に関しても支持されており、「85 percent disagreed with the statement that “it’s not cool to study real hard for tests and quizzes,”」とあるため、圧倒的多数がテストやクイズのために一生懸命勉強することを受け入れていることが示されています。

  これらの引用に基づき、D「over four-fifths think it is not cool to volunteer answers in class.」が誤りであることがわかります。実際には、「81 percent of middle and high school students who were surveyed in 1998-1999 disagreed with the statement that “it’s not cool to frequently volunteer answers or comments in class,”」と記述されています。これは、四分の五以上の生徒がクラスで積極的に回答やコメントをすることを「かっこ悪い」とは思っていないことを示しており、選択肢Dが本文の内容と矛盾しています。

  2024年早稲田法学部英語大問3

  1 K
  2 L
  3 I
  4 G
  5 D
  6 C

  解答根拠

  1″to arrest you”：ここでは、”reason to”という構文が使われ、「あなたを逮捕する理由を与えたくない」という意味になります。これは、”to”を使って目的を表す典型的な英語表現です。
  2″with interfering with”：ここでの”charged with”は、「〜で告発されるいう意味を持つ表現です。
  3″of a sensitive”：ここでは、”information of a sensitive nature”という形で、「機密性の高い情報」という意味になります。”of”は、所有や種類を表します。
  4″from his workplace”：”stole from”は、「〜盗む」という意味のフレーズです。”from”はここで出所を示しています。
  5″away”：”run away”という熟語で、「逃げる」という意味あります。”away”は離れる動作を示します。
  6.at liberty to”：”at liberty to”は、「自由に〜するとができる」という意味の慣用句です。

  2024年早稲田法学部英語大問4

  1,D
  2,D
  3,C
  4,C

  解答根拠

  1,文中の(D)に文法的な間違いがあります。「a raise in their deaths」という表現は不適切です。「raise」は名詞として「昇給」などの意味で使われることが多く、ここでは「増加」を意味する「rise」という単語が適切です。したがって、正は「a rise in their deaths」となります。

  2,最後の部分である(D)「landfill is the only destination for other」が不完全です。正しくは、”others” もしくは “other types” とる必要があります。ここで言及されているのは数の「plastic types」なので、代名詞も複数形にするか、または “types” を明示する必要があります

  3,文中の(C)部分に文法的な間違いがあります。「each gestures」という表現が誤っています。”Each” は単数形を伴うので、正しくは “each gesture” となります。

  4,「that temporary illuminates」という表現が誤っています。”Temporary” は形容詞ですが、ここでは副詞が必要です。正しい形は “temporarily” となります。

  2024年早稲田法学部英語大問5

  1,C
  2,D
  3,E
  4,B
  5,E

  1「during a flight to New York City」という表現が最も自然で、事故がニューヨーク行きの飛行中に起きたことを示しています。

  2「When Avianca asked」という文脈では、アビアンカが裁判を棄却するよう求めた時点での出来事を指しているため、「When」が適切です。

  3複雑な連邦法に関する詳細な議論を指すのに、「with its detailed discussion」という表現が適しています。

  4,この文脈で「just」は、「その他は全て順調であったが、この一点のみが問題だった」というニュアンスを持たせています。

  5,スティーブン・A・シュワルツ弁護士が裁判所に対して告白したという文脈で、「on the mercy of the court」という表現が使用されます。これは、彼が裁判所に対して自分の過ちを認め、裁判所の慈悲を乞うている状況を示しています。

  出典:Here’s What Happens When Your Lawyer Uses ChatGPT in NYK

  2024年早稲田法学部英語大問6

  [分析中]

  2024年早稲田法学部英語大問7

  [分析中]

  2025年早稲田法を受ける人はどうするか？

  来年度受験を考えている人は、早稲田大学は共通試験の上位互換だと思ってください。
  一文一文を丁寧に読んでいたら終わりません。

  スキミング、スキャニングの能力をたかめ
  「要旨を掴む」、「該当箇所を探す」のを
  素早くできるような訓練をしていくのが必要になります。

  早稲田大学法学部を目指す上で、困りごとがあればお気軽にご相談ください。

早稲田大学国際教養学部が2/13に入試を迎えました。 このブログ記事では英語(Reading)の問題を分析していきます。 ページ目次2024年早稲田国際教養学部英語全体講評2024年早稲田国際教養学部英語大問12024年早稲田国際教養学部英語Ⅱ2024年早稲田国際教養学部英語Ⅲ 2024年早稲田国際

• …続きを読む
• 早稲田大学国際教養学部が2/13に入試を迎えました。

  このブログ記事では英語(Reading)の問題を分析していきます。

  [toc]

  2024年早稲田国際教養学部英語全体講評

  尋常でない難しさの大問1が出題された昨年度と比べると、読みやすくはなりました。

  ただ、このレベルの長文3つを時間内に解くの英語力としてはかなりの実力がないと難しいです。

  2024年早稲田国際教養学部英語大問1

  (1)
  1,F
  2,E
  3,G
  4,D
  5,H
  6,B
  7,C
  8,J

  (2)
  1 A
  2 B
  3 D
  4 E
  5 B
  6 E
  7 E
  8 C
  9 B
  10 D

  (3)
  ACEG

  大問1の解答根拠

  (1)
  1
  このパラグラフは、リングリング・ブラザーズ・アンド・バーナム＆ベイリー・サーカスが公演を終了するに至った複数の理由を概説しています。具体的には、運営コストの増加、人々の注意力の短縮、他のエンターテインメント形態の台頭、地方交通法規の影響、そして動物の権利に関する進化する対話によって、動物を使ったパフォーマンスが時代遅れであり、楽しいものではなくなっているとの認識などです。さらに、動物の扱いに関するマザー・ジョーンズの調査報告や、象のケアに関する訴訟があったことも触れています。これらの点から、サーカスの人気が衰える要因を概説しているため、選択肢Fが適切です。他の選択肢は、パラグラフに記載されている内容と直接関連しているとは言えません

  2
  このパラグラフは、P.T. バーナムとヘンリー・バーグの二人の主要人物に焦点を当て、バーナムはサーカスの創始者として動物の虐待を助長した人物と見なされがちである一方で、バーグとの関係を通じて動物の権利運動にも関与していたことを紹介しています。これは選択肢E「記事で議論されている二人の主要人物を紹介する」に該当します。バーナムとバーグの関係は、動物の権利運動の歴史において重要であり、その動きを支えるための注目を集めたことを強調しています。したがって、この二人の関係と彼らの活動を紹介する点でEが正しい選択肢となります。

  3
  このパラグラフはヘンリー・バーグの生い立ちと彼がアメリカ動物虐待防止協会（ASPCA）を設立した経緯を詳述しており、彼のバックグラウンドと動物の権利に対する彼の活動が中心となっています。バーグがどのようにして裕福な家庭の無為な息子から旅行中に目の当たりにした闘牛や馬車馬への虐待に動かされて活動家となったか、そして彼がニューヨークで動物虐待を取り締まる姿が説明されています。また、バーナムとの最初の公の論争についても触れられており、バーナムがサーカス業に参入する前から有名だったアメリカン・ミュージアムでのライブ動物の展示が紹介されています。他の選択肢はこのパラグラフの内容と直接関連していません。

  4
  ここで語られているのは、ヘンリー・バーグが法的措置をちらつかせながらP.T. バーナムに接触し、バーナムのスタッフが生きたウサギをボアコンストリクターに与えていることに対する抗議をした最初の出来事です。バーグは、支払い客の前で蛇に生きた獲物を食べさせるという「半野蛮」な実践を終わらせることを望んで博物館のスタッフに直接呼びかけ、バーナムに宛てた手紙の中で、もし蛇が他のものを食べることができないならば餓死させるべきだと主張しました。これは、バーグがバーナムに初めて法的措置を示唆した出来事を議論しており、選択肢Dが明確に当てはまります。他の選択肢はこのパラグラフの特定の内容には直接関連していません。

  5
  ヘンリー・バーグがボアコンストリクターに生きたウサギを餌として与えることに対して異議を唱えたにもかかわらず、バーナムがその慣習を続けると主張し、バーグに対して信じやすさや自己正当化を戒める応答をしたことが説明されています。また、バーグがこの問題でバーナムに屈することなく、ニューヨークの画期的な動物の権利法の下で執行権を授けられた後も、動物福祉のための仕事を続けたことが記されています。バーグが家畜の人道的な扱いのためにロビー活動を行い、犬や鶏の闘いに反対し、馬の疾病の流行中に動物のケアを提唱したことなど、彼が動物福祉に関する活動を続けた証拠が示されています。他の選択肢はこのパラグラフの内容に直接関連していないか、この具体的な状況を反映していません。

  6
  ヘンリー・バーグの努力がエリート層の政治的、慈善的な支援を受けていたにもかかわらず、彼が広範な一般大衆の支持を構築するのは遅かったと述べています。19世紀において、動物は一般に所有物と見なされており、所有者が自分の動物に何をするかはその人の事業と見なされていました。そのため、バーグが市内を巡って虐待を根絶しようとしても、多くの一般市民からは、高貴な人道主義者というよりも、詮索好きな貴族と見られていたと指摘しています。他の選択肢はこのパラグラフの内容に直接関連していないか、この具体的な状況を反映していません。

  7
  このパラグラフは選択肢C「バーナムが生きたデモンストレーションを使って、火の使用がサーカスの動物の安全と幸福に危険であるというバーグの主張を覆す方法を説明している」という記述を最もよく表しています。パラグラフには、バーナムが火を通じたパフォーマンスの危険性に関するバーグの主張に反論するために、実際に火の輪を通過するパフォーマンスを行ったことが記述されています。バーナムは自ら火の中に手を入れ、その後70歳にも関わらず、火の輪を通り抜けるパフォーマンスを見せました。さらに、バーナムはASPCAの監督官もこのパフォーマンスに招待し、彼らが馬の安全性に関して納得したことも説明されています。これは、バーナムが自己のショーの安全性を証明するために実際のデモンストレーションを使用したことを示しているため、選択肢Cが適切です。他の選択肢はこのパラグラフの具体的な内容とは直接関係がありません。

  8
  このパラグラフは選択肢J「バーナムとバーグが、時に意見の違いがあるにもかかわらず、友情が築かれたことを示している」という記述を最もよく表しています。パラグラフでは、バーナムが自伝でのパフォーマンスを振り返り、その時点でバーグや彼の議題を否定することを拒否したこと、そして彼の個人的な尊敬とバーグの高潔な仕事への称賛を損なわなかったことが述べられています。さらに、彼らの公の論争にもかかわらず、またはそれゆえに、二人が重要な歴史的瞬間に動物の権利擁護のプロファイルを高める温かく理解し合う友情を築いたことが強調されています。バーナムが社会の道徳的向上に向けて働くこと、そして社会的な原因を推進することに喜びを感じていたという点も指摘されており、これらの説明は選択肢Jの記述と一致します。他の選択肢はこのパラグラフの内容とは直接関係がありません。

  (3)

  A
  文書は、BarnumとBerghが生きたネズミではなく、生きたウサギをヘビに食べさせたことについて初めて衝突したと述べています。したがって、Statement Aは文書の記述と矛盾します。

  C
  Barnumが警察署長の馬の尾に火をつけたという記述は、実際にはBarnumが燃えるフープを通過するデモンストレーションを行ったことに関連しています。これは、動物に害を加える行為ではなく、Berghの懸念を覆すためのものでした。従って、Statement Cは文書の内容と矛盾します。

  E
  サーカスの運営年に関する詳細が不正確であるか、文書内で直接的に扱われていない情報を含んでいる可能性があります。文書はRingling Bros and Barnum & Bailey Circusが2017年に閉幕したことを述べていますが、Statement Eに含まれる情報が文書の範囲や文脈と完全に合致しない場合、これが4番目の矛盾する記述となる可能性があります。

  G
  BerghがASPCAを創設した後に船舶事業に転じたという記述は文書には見当たりません。この記述はBerghの活動に関する文書の記載と矛盾しています。

  出典

  Betsy Golden Kellum, “How P.T. Barnum Helped the Early days of Animal Rights”

  https://www.theatlantic.com/entertainment/archive/2017/05/how-pt-barnum-helped-the-early-days-of-animal-rights/525489/

  覚えておきたい単語

  表現/構文/単語	意味/用途
  come out of semi-retirement	一時的な引退から復帰する
  bear one’s name	〜の名を冠する
  thrilled crowds	観衆を熱狂させた
  jumping through hoops	困難な課題に挑戦する（文字通りの意味では火の輪をくぐる）
  cordial acquaintance	心からの知り合い/友好的な関係
  ill-advised interference	考えの足りない干渉
  impair my personal regard	私的な尊敬を損ねる
  noble works	高潔な仕事
  public sparring	公然とした口論
  a warm and knowing friendship	暖かく理解ある友情
  elevated the profile	プロファイルを高める
  moral improvement of society	社会の道徳的向上
  for all his flaws	彼の欠点にもかかわらず
  carry one’s own boat	自分の利益になる
  the final bow	最後のカーテンコール/終わりの挨拶
  behind the final curtain	舞台裏で

  2024年早稲田国際教養学部英語Ⅱ

  (1)
  1 C
  2 E
  3 F
  4 H
  5 I
  6 D
  7 G
  8 B

  (2)
  1 A
  2 A
  3 B
  4 D
  5 C
  6 B
  7 E
  8 A
  9 B
  10 A

  (3)
  A,C

  Ⅱの解答根拠

  (1)

  パラグラフ1では、「Kleist described his new power to at least five persons… None was able to reproduce his results.」と述べられています。これは、クライストが行った実験が他の人々によって再現されることが難しかったことを説明しています。
  パラグラフ2で、「He had forgotten to emphasize the counterintuitive step that made a condenser from a nail in a bottle… Without this prescription…」と述べられており、レーデン瓶実験を再現できなかった初期の理由について説明しています。
  パラグラフ3で、「Here the lawyer Andreas Cunaeus intervened… he let the genie out of the bottle.」とあり、クナイウスがレーデン瓶実験を再現できるようになったことが語られています。
  パラグラフ4では、「These exaggerations suggest how flagrantly the action of the condenser violated received ideas about electricity.」とあり、レーデン瓶の動作が当時の電気理論では未来の実験結果を予測できないことを示していると指摘しています。
  パラグラフ5で、「Frank admissions that the jar shattered accepted theory appeared on every hand.」と述べられ、「It appeared that the Leyden experiment was “different in kind” from the classical repertory of experiments in electricity.」と続けられています。これは、レーデン瓶に関する実験が全く新しい種類のものであると多くの人々が認めたことを示しています。
  パラグラフ6では、「Physicists found three ways besides external coating to enlarge their shocks…」とあり、より強い電撃を生み出すために使用されたいくつかの実験装置について詳細に説明しています。
  パラグラフ7で、「Let a gentleman hold the jar and a lady the prime conductor; both feel the shock when they touch.」そして、「Nollet shocked 180 soldiers in the same presence.」とあり、大勢の人々を使った公開実験がレーデン瓶からの電荷がどの回路をたどるかを決定するために使用されたことが言及されています。
  パラグラフ8では、「The charged jar was also intriguing when innocently insulated. It unaccountably preserved its punch for hours or even days…」とあり、レーデン瓶が長時間にわたって電荷を保持できるという事実が説明を超えていると主張しています。

  (2)

  1,この文脈において「veteran」は長年の経験を持つという意味で使われています。
  2,「grounded」は電気的な文脈で接地された、つまり大地に接続されたという意味で使われています。
  3,この場合の「prescription」は、処方箋や推奨される手順という意味ではなく、指示や命令という意味で用いられています
  4,文章中で「knocking down children」は文字通りの意味で使われており、電撃によって子供たちが実際に倒れたことを指しています。
  5,「violated」は、この文脈においては「破った」や「違反した」という意味ではなく、既成の理論に反した、すなわち「contradicted」に相当する意味で用いられています。
  6,「authority」は、この文脈で権威や支配者というよりは、専門家やエキスパートという意味合いで使われています。
  7,「classical」は、ここでは洗練されたや人文的という意味ではなく、標準的な、典型的な、従来の実験に使われる「standard」という意味です。
  8,「proposition」は、提案やスキームというよりは、主張や断言という意味で使われています。
  9,この文脈での「train」は、列車や運動という意味ではなく、一列に並んだ人々、すなわち「line」の意味で使用されています。
  10,presupposed」は、推論されたや法的に認められたというよりは、ある事が前提とされた、すなわち「assumed」という意味で使われています。

  (3)

  A. Electricians found that a Leyden jar has to be made out of glass.
  この文は誤りです。6パラグラフに「Nollet found that the shape of the vessel did not matter but that its substance had to be glass or porcelain.」とあるため、レーデン瓶はガラスだけでなく磁器でも作られることがわかります。

  B. Ewald J. von Kleist first invented what became known as the Leyden jar, but initially it was difficult for others to reproduce his experiment.
  この文は正しいです。1パラグラフに「Not until March 1746, three months after Kleist had announced his striking news, did anyone working from his instructions succeed.」と述べられており、クライストがレーデン瓶を最初に発明したこと、そして他の人々が彼の実験を再現することが当初は困難であったことが示されています。

  C. The length of time that a Leyden jar holds a charge can be increased by connecting them in parallel.
  この文は誤りです。6パラグラフには「Daniel Gralath connected jars in parallel into what he called a “battery”;」とありますが、これは電荷を長く保持するためではなく、衝撃を大きくするための方法として記述されています。

  D. The phenomena produced by the Leyden jar invalidated the theories of electricity that were current in the mid-18th century.
  この文は正しいです。5パラグラフに「Frank admissions that the jar shattered accepted theory appeared on every hand. Musschenbroek, hitherto an authority, now “understood nothing and could explain nothing” about electricity.」とあることから、レーデン瓶によって生じた現象が当時の電気の理論を無効にしたことが示されています。

  出典

  J.L Heibron “Elements of Early Modern Physics”

  2024年早稲田国際教養学部英語Ⅲ

  Ⅲ
  (1)
  1 G
  2 I
  3 E
  4 D
  5 C
  6 J
  7 F
  (2)
  1 B
  2 E
  3 A
  4 A
  5 B
  6 D
  7 C

  (3)
  CEGH

  Ⅲの解答根拠

  (1)

  段落1では、エルスペス・スタッキーの1991年の著書「The Violence of Literacy」が1995年に菊池久一によって日本語に翻訳されたこと、そしてその翻訳が日本の社会言語学において影響を与えたことが述べられています。
  段落2では、研究者の砂野幸稔が「単一の識字」の覇権的な力を研究し、それを社会的排除のメカニズムとして分析していることが述べられています。また、識字を近代、イデオロギーの装置、排除のメカニズムとしての3つの視点から解説しています。
  段落3では、識字の排除機能による社会的排斥を通じた非識字者へのスティグマが、ユネスコや他の機関が無意識のうちに再生産してしまっていると述べられています。これは、識字の「排除の機能」が、たとえ善意からの努力であっても、そのようなキャンペーンを通じて解決されていないことを意味しています。
  段落4では、「文字盲」という言葉が非識字と障害とを結びつけていると指摘し、また識字研究が障害を持つ人々の識字問題を避けていると述べています。
  段落5では、1948年に行われた広範囲に及ぶ識字調査の方法と、その結果が99%という識字率の神話を作り出すためにどのように使用されたかを説明しています。
  段落6では、識字調査の結果が、かなの使用を推進する者と漢字の使用を維持する者との間で行われた「国語・国字問題」の議論にどのように利用されたかを述べています。
  落7では、「1948年、障害を持つ人々は教育システムに登録されておらず、その結果、多くの人が一生非識字のままでいた」と述べており、このことから彼らが識字率の調査から除外されていたことがわかります。また、「彼らの非識字は、識字神話を支えるために隠されていた」とも述べられています。

  (2)

  1,「hegemonic」は「覇権的な」という意味で、支配的、優勢な力や影響力を指す。
  2,「enlightenment」は啓蒙主義を指し、近代的な価値や思考、理性、自由などの概念と関連している。
  3,「demarcation」は明確な区別や分類を意味する。
  4,「inadvertently」は意図せずに、偶然にという意味である。
  5,「philanthropic」は慈善的な、善意に基づく行為を指す。
  6,「this notwithstanding」は「それにもかかわらず」という意味で、前の文の内容に反するが、という接続詞的な役割を果たす。
  7,「tenable」は持続可能、または正当化できるという意味

  (3)

  了解しました。それでは、各選択肢が文章と合致するか矛盾するかを確認し、具体的な段落と引用を用いて説明します。

  A. An important survey on Japanese literacy rates was undertaken during the US occupation.
  これは文章と一致しています。段落5には次のように記述されています:
  “The main pillar of this myth is a survey conducted after WWII under the US occupation.”

  B. Official statements made by the Japanese government have spread false information about Japanese literacy rates around the world.
  これも文章と一致しています。段落6には次のように記述されています:
  “This myth then spread around the world.”

  C. People with mental and physical disabilities are usually excluded from statistical surveys conducted by international organizations.
  これは文中で言及されていません。しかし、段落7には特定の1948年の調査に関連して次のように記述されています:
  “In 1948, people with disabilities were not enrolled in the education system; many remained illiterate for their entire lives as a result.”
  これは国際機関が実施する調査において常にそうであるとは述べていないため、Cは文章と矛盾します。

  D. The concept of literacy can function as a way to control people.
  これは文章と一致しています。段落1には次のように記述されています:
  “Literacy, he maintains, monopolizes the construction of social knowledge.”
  これは識字が人々をコントロールする方法として機能することを示唆しています。

  E. The high literacy rate of Japan is considered to be declining because of a new research methodology aligned to the global standard.
  これは文中で述べられていません。文中では、識字率が高いという「神話」が問題視されていますが、新しい研究方法論が原因であるとは述べられていません。したがって、Eは文章と矛盾します。

  F. There was a time when some people proposed discontinuing the use of kanji in the Japanese writing system.
  これは文章と一致しています。段落6には次のように記述されています:
  “Some placed a high value on the phonographic writing system and argued to abolish kanji altogether.”

  G. UNESCO and other institutions are viewed to have liberated the oppressed in modern societies by eradicating illiteracy.
  これは文中で述べられていません。段落3では、ユネスコと他の機関が識字の排除機能を無意識のうちに再生産してしまっていると述べており、抑圧を解放したとは言及されていません。したがって、Gは文章と矛盾します:
  “The stigma of being illiterate emerges as the result of social rejection through the exclusionary function of literacy.”

  H. Western-style schooling was rejected in Japan because it was felt that the difference in writing systems made it inappropriate.
  これは文章と矛盾しています。段落1では、西洋式の学校教育が権力構造によって保護され、促進されていると述べられています:
  “They criticize the privileged position of western-style school literacy, which is protected and promoted by powerful institutions.”
  これは西洋式学校教育が不適切であると感じられ、拒否されたとは反対の主張です。

  出典

  Takeshi Nakashima “Literacy and Illiteracy” in Rutledge Handbook of Japanese sociolinguistics

ページ目次早稲田社会科学部合格最低点(25年分)から見る合格シナリオ|早慶専門塾が監修早稲田社学合格最低点推移早稲田社学｜各科目別受験者平均点【社学】合格点を取るためには？早稲田社学で重要になる科目は？早稲田大学社会科学部に圧倒的な実力で合格できる専門対策をします 早稲田社会科学部合格最低点(25年

• …続きを読む

• 早稲田社会科学部合格最低点(25年分)から見る合格シナリオ|早慶専門塾が監修

  本ブログ記事では早稲田大学社会科学部の合格最低点、
  受験者平均点から入試でどのように対策をしていけば良いのかをお伝えしていきます。

  [toc]

  早稲田社学合格最低点推移

  下記より早稲田大学社会科学部の合格最低点の推移をお伝えしていきます。

  年度	配点	合格最低点	得点率
  2023	130	78.92	60.71%
  2022	130	89.451	68.81%
  2021	130	78.62	60.48%
  2020	130	91.36	70.28%
  2019	130	85.50	65.77%
  2018	130	82.95	63.81%
  2017	130	89.52	68.86%
  2016	130	77.10	59.31%
  2015	130	85.05	65.42%
  2014	130	83.15	63.96%
  2013	130	78.52	60.40%
  2012	130	83.10	63.92%
  2011	130	85.90	66.08%
  2010	130	86.00	66.15%
  2009	130	76.20	58.62%
  2008	130	93.60	72.00%
  2007	130	85.50	65.77%
  2006	130	93.50	71.92%

  早稲田社学｜各科目別受験者平均点

  • 英語:50点
  • 他の科目:40点

  英語と国語の平均得点と得点率

  年度	英語	英語得点率	国語	国語得点率
  2023	20.930	41.86%	22.378	55.945%
  2022	24.159	48.318%	28.945	72.363%
  2021	19.404	38.808%	24.158	60.395%
  2020	22.191	44.382%	30.603	76.508%
  2019	20.853	41.706%	25.824	64.56%
  2018	21.784	43.568%	23.936	59.84%
  2017	22.949	45.898%	27.900	69.75%
  2016	19.430	38.86%	21.987	54.968%
  2015	22.698	45.396%	26.425	66.063%
  2014	25.430	50.86%	21.586	53.965%
  2013	20.698	41.396%	21.435	53.588%
  2012	22.954	45.908%	24.453	61.133%
  2011	26.976	53.952%	20.775	51.938%
  2010	25.713	51.426%	21.401	53.503%
  2009	20.062	40.124%	18.939	47.348%
  2008	26.046	52.092%	29.286	73.215%
  2007	26.700	53.4%	21.400	53.5%

  選択科目の平均得点と得点率

  年度	日本史	日本史 得点率	数学	数学 得点率	世界史	世界史 得点率
  2023	18	45%	15	39%	28	70%
  2022	22	55%	12	29%	25	63%
  2021	23	58%	18	46%	23	58%
  2020	21	53%	12	29%	22	55%
  2019	23	57%	21	52%	26	65%
  2018	17	43%	14	35%	24	59%
  2017	19	47%	14	34%	25	63%
  2016	20	51%	14	36%	24	59%
  2015	22	54%	17	41%	23	58%
  2014	22	54%	15	38%	21	53%
  2013	26	64%	13	33%	22	55%
  2012	19	47%	17	43%	22	55%
  2011	21	52%	11	28%	14	36%
  2010	24	60%	12	29%	20	49%
  2009	23	57%	16	39%	18	46%
  2008	22	56%	16	39%	20	49%
  2007	23	58%	26	66%	19	48%

  【社学】合格点を取るためには？

  全期間(2007年-2023年)

  • 合格最低点の平均点: 84.49点
  • 平均得点率: 65.30%

  過去5年間(2019年-2023年)

  • 合格最低点の平均点: 83.726点
  • 平均得点率: 65.53%
  

  全年度をみても直近の年度を見ても65%の点数を取れば良いことがわかります。

  科目ごとで受かりやすさを考える

  早稲田入試でよく出るのが成績標準化問題ですが、

  早稲田社学は選択科目のみでの標準化となります。

  全期間(2007年-2023年)の平均得点率

  • 日本史: 52.738%
  • 数学: 36.091%
  • 世界史: 54.248%

  過去5年間(2019年-2023年)の平均得点率

  • 日本史: 49.765%
  • 数学: 38.147%
  • 世界史: 62.542%

  商学部と同じように数学が難しい。
  日本史、世界史は点数は大体同じくらいです。年によりどちらかが簡単な年があります。

  早稲田社学で重要になる科目は？

  早稲田大学社会科学部に合格するために重要になってくる科目は、英語です。

  早慶で合格したいのであれば、英語での高得点が必須なんですね。

  

  目標得点は35点です。
  急に難しくなったりと変動が出やすいのですが、語彙力を高めておくことで合格までの道筋は見えてきます。

  社学用の単語帳はこちらでまとめました。
  [nlink url="https://hiroacademia.jpn.com/blog/taisaku/waseda/syagaku/waseda-syagaku-english-tangocho/"]

  国語は受験者平均点で６割近くと結構高めの点数です。
  こちらも30点を安定して取れるように勉強を積んでおく必要があるでしょう。

  早稲田社会科学部その他具体的な対策

  早稲田大学社会科学部のその他具体的な対策のページはこちらよりご覧ください。

  社会科学部入試データ
  英語対策
  国語対策
  世界史対策
  日本史対策
  数学対策

  早稲田大学社会科学部に圧倒的な実力で合格できる専門対策をします

  まずは資料請求・お問い合わせ・学習相談から！

  早慶専門個別指導塾HIRO ACADEMIAには、早稲田大学専門として社会科学部への圧倒的な合格ノウハウがございます。

  少しでもご興味をお持ちいただいた方は、まずは合格に役立つノウハウや情報を、詰め込んだ資料をご請求ください。

  また、早稲田大学社会科学部に合格するためにどのよう勉強をしたらよいのかを指示する学習カウンセリングも承っています。学習状況を伺った上で、残りの期間でどう受かるかを提案いたしますので、ぜひお気軽にお電話いただければと思います。

  ⇒早稲田大学社会科学部に合格したい方は、まずは当塾の資料をご請求ください。

  [ad doc=""]

早稲田に合格するために必要な長文能力とは？ 今回のブログでは、早稲田の英語長文に絞って解説していきます。 長文を読む＝問題を解くことをイメージしてしまいがちですが、、 実際には、早稲田レベルの本格的な問題を解く前に やっておいてほしいことがいろいろあります。 下記4つの観点から、英文をどのような点か

• …続きを読む

• 早稲田に合格するために必要な長文能力とは？

  今回のブログでは、早稲田の英語長文に絞って解説していきます。

  長文を読む＝問題を解くことをイメージしてしまいがちですが、、

  実際には、早稲田レベルの本格的な問題を解く前に

  やっておいてほしいことがいろいろあります。

  下記4つの観点から、英文をどのような点から見ていくのか見ていきましょう。

  またこの4つの観点に当てはまる英語長文の参考書についても紹介していきます。

  見るべき4つの点とは？

  • 精読力
  • つながりを読み解く力
  • 速読力
  • 解く力

  

  ▶︎精読力(早稲田の長文に必要な力1)

  精読とは、一文を正しく文法的に読み下せる力です。

  例えば、下記文章を文法的に正しく読めるように見てみましょう。

  No one predicted that the project would become a defining feature of his foreign policy and dramatic symbol of China’s rise as a global power.

  引用:The path ahead for China’s Belt and Road Initiative from TheEconomist

  

  大体英語が苦手な子だったり、受験勉強をしてなかったこだとこんな感じで、

  SVOだけ何となくつけた感じで処理されてしまいます。

  残念ですが、それではダメです！

  SVOだけでなく、句、節といった細かい分類までできるようにしてください。
  そうすると、 こんな感じになります。

  
  こんな感じで、詳しく一文一文を読めるようにしていくのが、

  英語長文を読めるようになる第一歩になります。

  • できる限り、細かく文構造を取れるようにしていってください。

  この辺りの精読をすべての文章でできるようにしてくのが重要になります。
  詳しい参考書はこちらの記事にで紹介してるので、ご覧ください。

  [nlink url="https://hiroacademia.jpn.com/blog/sankosyo/eigo/sokei-englishinterpretation/"]

  ▶︎つながりを読み解く力(早稲田の長文に必要な力2)

  1文がちゃんと読みこなせるようになってきたら、

  文章同士のつながりを理解できるようにならなくてはいけません。

  文章同士のつながりというのは具体的には、
  下記のような文章を見てください。

  1文の文章があって、
  その次にもう一文Thisから始まる下記のような文章があります。

  I bought a new bicycle yesterday. This is my third one.

  このThisが何を指しているのか？と考えるのが文章のつながりを考える力になります。
  今回のような簡単な文章であれば、間違える人はいないと思いますが、、

  偏差値60以上の生徒でも少し難しい文章になった場合には、

  Thisが何を指しているのかを躊躇してしまう子が多いのです。

  例えば下記文章に変換された場合、、

  Having nurtured an ever-deepening affinity for the thrill of cycling, I, amidst a myriad of choices and after much contemplation, opted to acquire a new bicycle just yesterday. This acquisition represents the third of its kind in my personal collection.

  This acquisitionが何を指しているのかを考えずに、次の文章に進んでいってしまう人がいるのです。
  ＊今回は一文目のacquireのまとめを表しています。

  文章のつながりを理解するためには、
  このような形で一文一文丁寧に何を指しているのかを考えていくのが重要です。

  今回、確認した代名詞以外にもディスコースマーカーや定冠詞によるつながりを
  わかるようになっていくのは重要です。

  注意点

  文章のつながりがわからないと、
  早稲田大学の長文で頻出の空欄補充問題や未知語の類推ができなくなってしまいます。

  つながりを読み解く力をつける参考書

  文章のつながりを理解するための知識、演習をすることができる参考書を具体的にみていきましょう。
  

  そもそもがこのレベルを実施ができる段階ということを考えると、

  必然的に参考書自体のレベルは高くなってしまいます。

  どの教材もおすすめですが、自習用で進めるというのであれば、

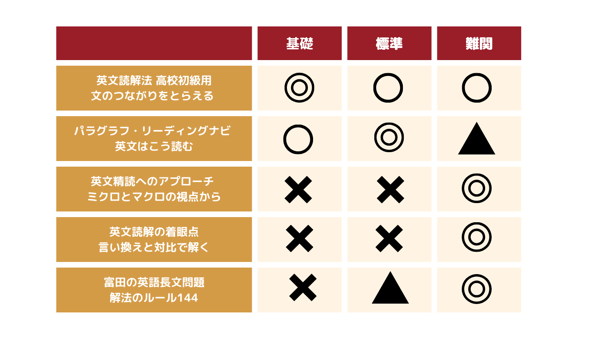
  「英文読解法　文のつながりを捉える」、「パラグラフリーディングナビ」がおすすめです。

  [itemlink post_id="19210"] [itemlink post_id="22328"]

  「英文精読のアプローチ」、「英文読解の着眼点」、は

  対象読者のレベルが高いので、人によっては使うのが難しいかもしれません。

  [itemlink post_id="22330"] [itemlink post_id="22331"]

  富田先生の教材は、長文を解きながら進めていくスタイルで
  文章のレベルもそこまで高くないものから始まっているので、
  取り組みはしやすいです。

  [itemlink post_id="22332"]

  ▶︎速読力(早稲田の長文に必要な力3)

  大学入試の英語で問題が解けるようになるためには、

  時間内に読むことができる「速読力」が必要です。

  大学受験で必要な「速読力」とは？

  大学受験レベルで重要な速読力は、いたずらに早く読むことができる能力ではありません。

  内容をほとんど理解せずともできる共通テストのように、

  探すように処理ができる場合のような長文は、

  早稲田の大学受験で問われません。

  ではどうするのか？というと、

  ここまで学んできた精読、文章のつながりを

  完璧にわかるように早く処理ができるようにすることです。

  一番のおすすめは「ぐんぐん伸びる英語参考書」です。

  読解の神書「ぐんぐん伸びる英語参考書」とは？

  [itemlink post_id="22333"] [itemlink post_id="22334"] [itemlink post_id="22335"]

  長文の読み込みをひたすら行っていく教材です。

  構文の詳しい説明や、

  どの点が抽象で具体的な部分なのかを理解することができる教材です。

  英語を読む上で、どこが抽象的で具体的なのかというのを理解するのは必須なのですが、、

  この点について説明してる教材は、ほとんどないのが現状です。

  名詞、動詞を使った具体抽象度の判定

  文章の順序(倒置)の意味などかなりレベルの高いことにも触れているので、

  本書で述べられていることをマスターしていきましょう。

  長文を読む時に何も意識をしないで読むことに終始しがちです。

  英文を読む時に意識してほしいことを本書には詳しく記載していますので、

  ぜひ徹底的な読み込みをしてみてください。

  また専用サイトを用意して、WPMで測って速度を意識ができることができます。
  

  読み込みの具体的な回数はどれくらいすれば良いのか？

  少なく見積もっても、
  一つの長文につき通算100回以上は読み込みを行うようにしてください。

  英語が速く読めないという人は、効果を速く求めすぎです。

  同じ教材を何度も何度も意識化をして読み込みをしていくことで、

  読む速さ、処理速度は徐々に上がっていきます。

  その他ぐんぐんをクリアして余裕のある人がやっておく教材です。

  宮下先生の「大学入試 英語長文プラス 速読トレーニング問題集」 も

  どのような点を省いていくと速く読めるかを理解するには重要な教材です。

  余裕のある人はやってみても良いと思います。

  [itemlink post_id="20070"]

  その他、共通テストが苦手な人はこちらの教材をやっておくと良いでしょう。

  速読マスター　標準編　発展編

  [itemlink post_id="22336"] [itemlink post_id="22337"]

  パラグラフリーディングの体系的な理解をしたい人はこちらもおすすめです。

  パラグラフリーディングのストラテジー 1

  [itemlink post_id="22338"]

  難しい長文をそのトピックと一緒に読み込んでいきたいのであれば、下記がおすすめです。

  速読英単語　上級編

  上級英単語 LOGOPHILIA ロゴフィリア

  [nlink url="https://hiroacademia.jpn.com/blog/sankosyo/eigo/logophilia/"] [itemlink post_id="22339"] [itemlink post_id="22340"]

  ▶︎解く力(早稲田の長文に必要な力4)

  上記までの段階をクリアしたら解く力を強化するために、
  問題を解いていきましょう。
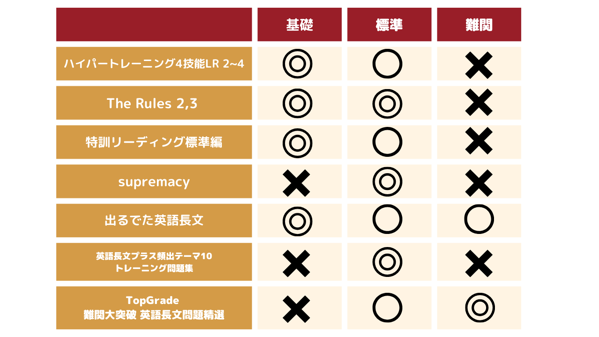
  下記が解いてほしい教材です。もちろん全て解く必要はありません。
  

  どれも素晴らしい参考書ばかりですが、

  優先的にやっておいた方が良いのは、

  「The Rules2,3」(記述が少ない早稲田であれば、無理して難しい4までやる必要はありません。)です。

  [itemlink post_id="22341"] [itemlink post_id="22342"]

  まずはこの教材のやり込みが必須ですね。

  注意

  教材は、たくさんやればやるほどいいわけではないので注意してください。
  一冊の教材の読み込みが足らないといつまで経っても速く読めるようになりません。

  本当に英語が苦手・・・という人は、

  「ハイパートレーニング 4技能LRの2~4」をやってみて文構造を取るのが良いでしょう。

  [itemlink post_id="22343"]

  上記以外で別口でやっておいてほしい英語長文教材、「佐藤ヒロシの英語長文が面白いほどとける本(マーク編)。

  [itemlink post_id="22344"]

  こちらについては、選択肢の処理の仕方を学ぶことができるので、

  記述はできるんだけど・・・マークになるとダメだ、

  という人はこちらの教材をやってみると良いでしょう。

  紹介した英語長文参考書一覧

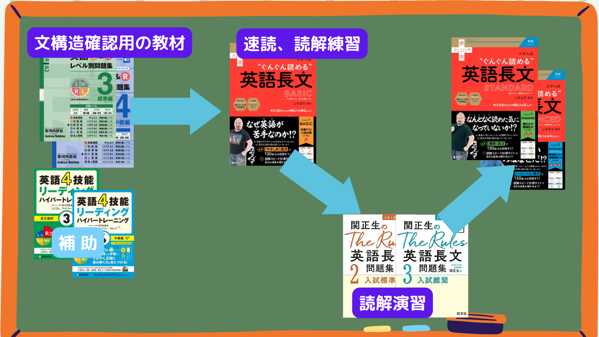
  [itemlink post_id="22345"] [itemlink post_id="22346"] [itemlink post_id="22347"] [itemlink post_id="22348"] [itemlink post_id="22349"]

  早稲田を目指すための長文参考書の順番は？

  ここまで色々と教材はお伝えしてきましたが、
  最短での早稲田長文への順番はこんな感じです。
  

  「これだけでいいの！？」と思うかもしれませんが、、、

  実際には英単語、英熟語、英語構文、英作文などを並行して勉強していく必要があるので、
  思っている以上にやることは多いです。

  長文以外でどんなおことをやるのか？という人はこちらの早稲田に合格するためにすることを書いた記事をご覧ください。

  [nlink url="https://hiroacademia.jpn.com/blog/taisaku/waseda/waseda-eigo-benkyohou/"]

  もちろん、他の英語長文教材に色々と手を出す余裕があるのであれば、実施した方が良いのですが、

  ほとんどの人がオーバーワークになってしまいます。

  英語長文は色々と手を出すよりもまずは、
  一つの長文を読み込むことに力を入れてください。

  早稲田で別途対策が必要な学部一覧

  ここまでで早稲田の基本的な英語力をつけることができる教材をお伝えしてきました。

  お伝えした教材を完璧にやりこんでもらえれば、

  ほとんどの学部はあとは過去問で対応可能です。

  早稲田国際教養、文学部、文化構想学部、といった要約問題がある学部は、

  要約対策で下記のような教材をやってみても良いでしょう。

  もちろん必須ではないです。

  それ以外の学部だと、法学部や国際教養、超長文の練習を過去問以外で積みたいとなれば、

  やっておきたい英語長文1000をやってみると良いでしょう。

  [itemlink post_id="22350"]

  社会科学部を目指すのであれば、単語力の強化が必須です。
  ＊昨今の入試の状況をみると商学部も単語の異常な難しさになろうとしていることがわかります。
  このような学部を受ける場合は別途対策が必要です。
  下記のような単語帳を使って覚えていくのが良いでしょう。
  [nlink url="https://hiroacademia.jpn.com/blog/taisaku/waseda/syagaku/waseda-syagaku-english-tangocho/"]

  単語力を強化しつつ、下記のようなサイトで英語の記事を読んでいくのが良いでしょう。
  ＊TIMEはオンライン版が無料になったので、ぜひ読んでみてください。
  早稲田の入試でも頻出です。

  • The Economist
  • Foreign Affairs
  • TIME
  • NewYork Times

  早稲田の英語長文を絶対的な得意のレベルにしたい場合は？

  ここまで色々とみてきましたが、

  早稲田大学に合格するとなるとかなりのレベルの学力が必要なことは間違いありません。

  現状の学力とあっていない教材をやってしまうことによって学力は、

  上がるどころか停滞していきます。

  自身の学力に合わせて、適切な勉強をしていくようにしていきましょう。

  当塾では早稲田大学の英語長文に対してどの学力からでも対応することができます。

  お気軽にご相談ください。

  [ad doc=""]