ページ目次難関大に合格する英文解釈 Code 70とは?早慶・東大攻略の新定番難関大に合格する英文解釈 Code 70の基本情報と5つの特徴Code 70のレベルは?早慶・東大受験での位置付けCode 70の効果的な使い方・勉強法Code 70を使うメリットCode 70を使うデメリットCode 7
- …続きを読む
-
難関大に合格する英文解釈 Code 70とは?早慶・東大攻略の新定番
「早慶や東大の英語が難しくて全然読めない…」「英文解釈の参考書がたくさんあって、どれを選べばいいかわからない」

そんな悩みを持つあなたへ。2024年7月に発売された「難関大に合格する英文解釈 Code 70」は、早慶・東大・京大合格を目指す受験生にとって、まさに革命的な参考書となりえます。
しかし、その一方で、「本当に難関大レベルで必要?」「従来の参考書と何が違うの?」といった疑問も聞かれます。
この記事では、「難関大に合格する英文解釈 Code 70」の特徴やレベル感を徹底解説し、早慶・東大受験において、この参考書が本当に必要なのか、どのように活用すれば効果的なのかを具体的に解説していきます。
[toc]
著者の杉村年彦先生は「伊藤先生&薬袋先生の魂を受け継ぐ」と評される実力派講師です。
難関大に合格する英文解釈 Code 70の基本情報と5つの特徴
まず、「難関大に合格する英文解釈 Code 70」の基本情報を確認しましょう。
【基本情報】
– 著者:杉村年彦
– 出版社:かんき出版
– 発行日:2024年7月10日
– 定価:1,760円(税込)
– 判型:A5判
– 頁数:256頁本書は、他の英文解釈参考書とは一線を画す、以下の5つの特徴があります。
- クイズ形式で英文解釈のポイントが学べる
- 出題データの徹底分析に基づいた内容構成(過去20年間の難関大学問題を分析)
- 例文を含めほぼすべて、難関大学で出題された英文を引用
- 「間違えた読み方」にあえて言及した解説
- 速読につながる「よく使われる形」への言及
英文読解の上級レベルに不可欠なテーマを網羅的に扱っているので、基礎学力があればこれ一冊で難関レベルに対応可能です。

これらのテーマは、早慶・東大・京大の英語においても頻出であり、
本書をマスターすることで、複雑な構文を正確に読み解く力が身につきます。従来の英文解釈参考書との違い
「Code 70」が従来の参考書と大きく異なるのは、「クイズ形式」を採用している点です。
従来の参考書では「英文を読んで訳しなさい」という形式が一般的でしたが、本書では以下のようなクイズが設けられています。
例:「この英文のSVはどこですか?」「この文の主語は何ですか?」「なぜこの読み方ではダメなのですか?」
このアプローチにより、単純な暗記ではなく、英文解釈の「思考プロセス」を身につけることができます。
これまでの「訳をチェックするだけの勉強」から脱却できるのが大きなメリットですね!

早慶・東大の過去問でこんな英文に苦戦していませんか?
早稲田・慶應・東大・京大といった最難関大学では、以下のような特徴を持つ英文が出題される傾向があります。
読む時にここでつまづいていませんか?- 一文が非常に長い(100語を超える文も珍しくない)
- 複雑な構文が用いられている(倒置、省略、挿入など)
- 抽象的な表現や高度な語彙が使われている
- 文脈に依存する表現が多い
「難関大に合格する英文解釈 Code 70」は、まさにそうした高度な読解力を養うための最適な教材と言えるでしょう。
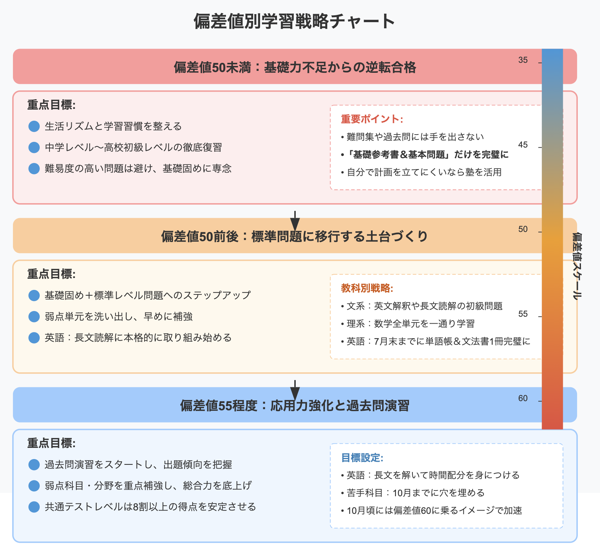
Code 70のレベルは?早慶・東大受験での位置付け
「難関大に合格する英文解釈 Code 70」は、標準レベル以上の文法を理解している人を対象としています。
具体的には、以下のようなレベル感が目安となります。- 共通テストレベルの問題を8割以上安定して解ける
- 河合の模試で英語の偏差値が65程度取れている
- 早慶の英語過去問に少し挑戦してみて、歯が立たないわけではないレベル
- 基本的な英文法(Forest、Vintage等)を一通り学習済み
本書は、基礎的な文法力を前提に、受験生が間違えやすい点や、難解な文章の解説が中心となっています。
基本的な文法事項に不安がある場合は、「Code 70」に取り組む前に、基礎を固めることをおすすめします。

皆がやっている難しい教材をやっているから受かるというわけでは決してないので要注意!
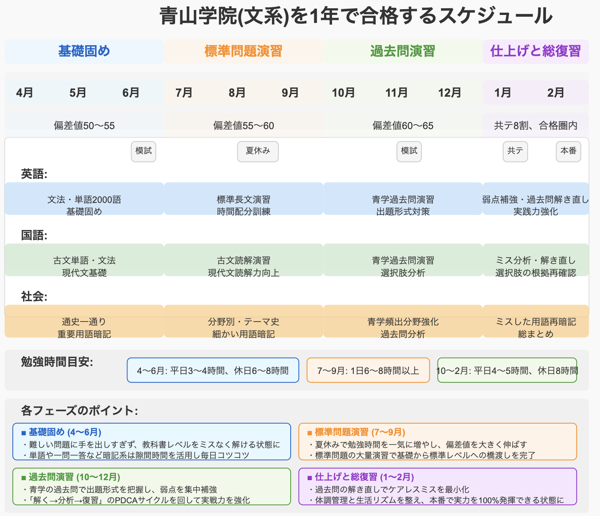
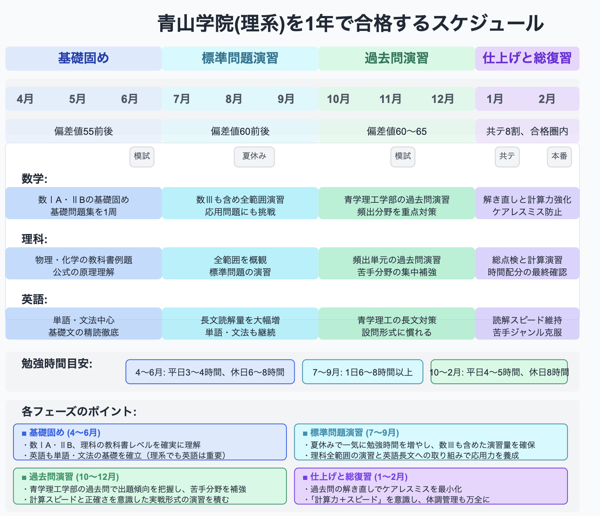
早慶・東大合格に向けたレベルアップ
早慶・東大・京大、特に英語難関学部を目指すなら、標準レベルの英文法・解釈問題集をマスターした後に取り組むのが効果的です。
具体的に、基礎から入試レベルまでの精読力をつけるためには「英文熟考上・下」がおすすめです。英文熟考を完璧にマスターした後に、Code 70に取り組むのが最も効果的な学習順序です。
英文熟考上・下の後にCode 70をやるべき理由
「英文熟考上・下」は標準レベルから難関大レベルまでの英文解釈を体系的に学べる優秀な参考書です。Code 70に取り組む前に英文熟考を完璧にしておくことで、以下のメリットがあります。
- 基本的な構文解釈のパターンが身についている
- SVOC の振り方が正確にできるようになっている
- 標準レベルの英文なら確実に読めるようになっている
- Code 70の高度な内容により集中できる
英文熟考上・下 → Code 70 → 過去問演習という流れが、難関大合格への最短ルートです。

志望学部によってはCode 70を行わなくても、英文熟考だけで十分な場合もありますよ
余裕のある人やさらに一段階上の読解力を身につけたい人は、「Code 70」を使うことで合格に大きく近づきます。
[nlink url="https://hiroacademia.jpn.com/blog/sankosyo/eigo/eibunjukuko/"]他の最難関レベル参考書との比較
同レベルの参考書として、以下のようなものがあります。
参考書名 難易度 特徴 英文読解の透視図 ★★★★★ 伝統的な解釈本、解説が詳細 ポレポレ英文読解プロセス50 ★★★★☆ コンパクト、西きょうじ先生の名著 Code 70 ★★★★☆ クイズ形式、最新の出題傾向反映 英文解釈の技術100 ★★★★☆ 体系的、例題が豊富 Code 70の効果的な使い方・勉強法
「難関大に合格する英文解釈 Code 70」を最大限に活用するため、以下の3ステップで学習を進めていきましょう。
ステップ1:基礎確認と理解
- 各講の英文を丁寧に読み込み、構文や文法事項を理解する
- クイズに答える前に、自分なりに英文を分析してみる
- クイズに答えて、自分の理解度を確認する
- 解説をよく読み、著者の解釈の仕方をつかむ
ステップ2:実践と定着
- 間違えた箇所は解説をよく読んで理解する
- 「間違えた読み方」の解説を特に重視する
- 定型表現や「よく使われる形」を積極的に覚える
- 構造図を参考に、SVOC を正確に把握する練習をする
各章は、文法的に難しいことから和訳に至るまで網羅的な難しい題材を取り扱っているので、英文解釈の力がついていきます。

ステップ3:復習と応用
- 間違えた問題を繰り返し解き、理解を定着させる
- 学んだルールを本書最後の「code一覧」で確認する
- 定期的に復習し、記憶の定着を図る
- 実際の過去問で学んだ技術を応用する
おすすめ使用期間は2か月〜3ヶ月程度です。
早慶・東大の過去問演習と並行して進めるのも効果的です。問題を解く過程で間違えた場合、その理由を突き止めて同じ間違いを繰り返さないようにするのは重要です。
Code 70を使うメリット
早慶・東大受験において「難関大に合格する英文解釈 Code 70」を使うメリットは以下の通りです。
「Code 70」のメリット- クイズ形式で思考プロセスが身につく
- 最新の出題傾向が反映されている(過去20年分の分析)
- 「間違えた読み方」の解説で、よくある誤読を防げる
- 定型表現の習得で速読力も向上する
- 解説が詳細で、独学でも効率的に学習できる
- 話し口調の解説で読みやすい
Code 70を使うデメリット
一方で、以下の様な点がデメリットとして挙げられます。
Code 70のデメリット- 初学者には難易度が高すぎて、基礎力がないと使いこなせない
- 音声がないため、リスニング対策にはならない
- 感覚的に英語を読んできた人には理論的すぎる可能性
- 受ける学部によっては、本書で扱う内容が難しすぎる場合もある
- 訳が少し見にくいレイアウト
基礎をしっかり固めた上で、志望学部に本当に必要かどうかを見極めてから使用しましょう。
Code 70は新しすぎて大丈夫?
2024年7月発売の新しい参考書ということで、「実績が不安」という声もあります。
しかし、著者の杉村年彦先生は、薬袋善郎先生や伊藤和夫先生の流れを汲む実力派講師として知られており、YouTube動画でも「神参考書誕生」と評価されています。
むしろ、最新の出題傾向を反映している点で、従来の参考書よりも有利と言えるでしょう。
Code 70と他の英文解釈参考書との詳細比較
vs 英文読解の透視図
「英文読解の透視図」は1993年発売の伝統的な英文解釈参考書として長年愛用されてきました。Code 70との違いを詳しく見てみましょう。
項目 Code 70 透視図 発行年 2024年 1993年 難易度 ★★★★☆ ★★★★★ 解説スタイル クイズ形式、話し口調 詳細な文法解説、硬い文体 ページ数 256ページ 約300ページ 取り組みやすさ 現代的でわかりやすい 古典的で重厚 出題傾向 過去20年分を分析 発売当時の傾向 透視図は非常に優秀な参考書ですが、30年前の参考書のため、現代の受験生には取り組みにくい面があります。Code 70は最新の出題傾向を反映しつつ、現代的な解説スタイルを採用しているため、より効率的に学習できます。
[nlink url="https://hiroacademia.jpn.com/blog/sankosyo/eigo/toushizu/"]vs ポレポレ英文読解プロセス50
「ポレポレ英文読解プロセス50」は西きょうじ先生の名著として知られています。Code 70との違いを詳しく比較してみましょう。
項目 Code 70 ポレポレ 問題数 70テーマ 50例題 解説の詳しさ 非常に詳しい(数ページ) 簡潔(1ページ程度) 学習期間 2-3ヶ月 1-2ヶ月 初学者向け ○(クイズ形式で段階的) △(ある程度の実力が必要) 独学のしやすさ ◎(解説が詳細) △(解説が簡潔すぎる場合も) コンパクトさ △(256ページ) ◎(129ページ) ポレポレは非常にコンパクトで効率的な参考書ですが、解説が簡潔すぎて独学では理解が困難な場合があります。Code 70は解説が詳しく、クイズ形式で段階的に理解を深められるため、独学者により適しています。
*ポレポレは西先生が動画教材を出しているので、そちらをみるのもOKです。
[nlink url="https://hiroacademia.jpn.com/blog/sankosyo/eigo/porepore/"]どちらを選ぶべき?参考書選択の指針
Code 70がおすすめな人- 独学で英文解釈を学びたい
- 詳しい解説で理解を深めたい
- 最新の出題傾向に対応したい
- 段階的に実力を上げたい
- 思考プロセスを重視したい
ポレポレ・透視図がおすすめな人- 短期間で仕上げたい(ポレポレ)
- 伝統的な解釈法を学びたい(透視図)
- 予備校で指導を受けている
- すでにある程度の実力がある

個人的には、現代の受験生にはCode 70が最も取り組みやすく、効果的だと感じます。
Code 70は早慶のどの学部で必要?
早慶・東大を受けたい…から難しい問題を解くという必要はありません。下記にCode 70が必要な学部を列挙しておきました。
早稲田大学
早稲田大学 Code 70が必要かどうか 政治経済学部 △ 法学部 ○ 文化構想学部 ○ 文学部 ○ 教育学部 △ 商学部 ◎ 基幹理工学部 ◎ 創造理工学部 ◎ 先進理工学部 ◎ 社会科学部 ◎ 人間科学部 × スポーツ科学部 × 国際教養学部 ◎ 慶應義塾大学
慶應義塾大学 Code 70が必要かどうか 文学部 ◎ 経済学部 ○ 法学部 ○ 商学部 △ 医学部 ○ 理工学部 △ 総合政策学部 ◎ 環境情報学部 ◎ 看護医療学部 × 薬学部 △ 理系は他の科目との兼ね合いを考えて余裕があればやってください。早稲田商学部、社学は文章が難解ですが、単語量と時間の兼ね合いになるでしょう。

Code 70の評判・口コミ
実際に「難関大に合格する英文解釈 Code 70」を使用した人たちの評価を見てみましょう。
Amazon レビューでの評価
「MARCH以上を狙っていて且つ英語が得意な人はやるべきだと個人的には感じた。難易度は英文塾講下の少し上くらい。解説もかなり詳しく書かれている。」(★★★★★)
「入試の構文としてはポレポレや透視図などと最高レベルです。アウトプット系参考書です。1つの例文に付いて解説が数ページあり詳しいです。」(★★★★☆)
予備校講師の評価
薬袋善郎先生(英語リーディング教本の著者)も以下のようにコメントしています。
杉村先生の『難関大に合格する 英文解釈Code 70』を読了しました。いろいろな優れた点がありますが、私は2点紹介したいと思います。… pic.twitter.com/YdQPcOoi7B
— 薬袋善郎 (@Ger81opi46) July 27, 2024
1つは「『教えたいこと』ではなく、『繰り返し出題されていること』に徹底的にこだわりました」という点です。問題集ではなく、このような英文解釈の参考書では、これはなかなかできないことです。難関大の過去20年間の問題の分析から抽出された「繰り返し出題されていること」は、受験生にとっては非常に価値のある情報です。これを1冊で集中して学べるのは、多くの科目を効率的に勉強しなければならない受験生にはとてもありがたいことです。もう1つは、課題の英文中に含まれている重要個所を説明するだけでなく、その重要個所を「拡大したパースペクティブ」から捉えていることです。たとえば、the skills and manpower necessary to make …という個所、本文でnecessaryの修飾関係を説明すると、すぐにそこに「形容詞の後置修飾 頻出5パターン」というコラムを置いて、本文の「名詞 形容詞 to do ~」を含めて5つのパターンを丁寧に解説している。このように類似の形を一覧的にまとめて勉強すると、異同がよくわかって、実戦力がつく。
このような「重要個所を拡大してまとめるコラム」は、全編にわたって、いろいろ出てきます。一部をタイトルだけ紹介すると「5文型の変化形」「複合関係詞節における省略」「強調構文のよく使われる形」「no more ~ than …系の完全理解」のような具合です。このコラムは、著者が読者のために作ってくれたサブノートのようなものです。これを受験勉強の最初から手中にできるのは、読者の大きなメリットです。全体をやり終えたら、「課題と本文」だけを通して読む、「コラム」だけを通して読む、といった読み方も考えられます。
『黄リー教』を終えた受験生が次にやるのに適した本として、推薦します。
Code 70以外のおすすめ参考書
上級レベルの英文解釈教材として名高い本書ですが、このレベルの教材については以下の選択肢もあります。
- 英文読解の透視図(より難解な分野に絞っている)
- ポレポレ英文読解プロセス50(コンパクトで実践的)
- 英文解釈の技術100(体系的で例題豊富)
- 解釈ポラリス2(関正生先生の最新作)
時間に余裕がある人は「英文解体新書」、「英文解釈教室」をやるのもおすすめします。
ヒロアカでは英文解体新書まで行って、早慶レベルの英語で無双してもらっています。

個人的には、現代の受験生にはCode 70が最も取り組みやすいと感じます。
まとめ:Code 70で難関大合格を目指そう
「難関大に合格する英文解釈 Code 70」は、2024年発売の最新参考書として、従来の英文解釈参考書の良いところを取り入れつつ、現代の受験生により適した形にアップデートされた優秀な教材です。
Code 70がおすすめな人- 早慶・東大・京大を目指している
- 基礎的な英文法は理解している(偏差値60程度)
- 英文解釈の思考プロセスを身につけたい
- 最新の出題傾向に対応したい
- 詳しい解説で独学したい
Code 70が向いていない人- 基礎的な英文法に不安がある
- 感覚的に英語を読みたい
- 短期間で仕上げたい
- 音声付きの教材を求めている
特に、早稲田国際教養学部、慶應文学部・SFC、東大・京大文系を目指す受験生には強くおすすめします。
英文解釈は一朝一夕には身につきませんが、「Code 70」で正しい思考プロセスを学べば、必ず難関大の英語を攻略できるようになります。
最後まで読んでいただき、ありがとうございました!Code 70で第一志望合格を勝ち取りましょう!

英語で成績が出なくてお悩みのそこのあなた!
当塾では、偏差値30からの早慶専門塾として、勉強してどうして成績が出ないのか?を完全に理解しています。英語には勉強のコツがあります。どのようにして英語の成果を上げるのか?対策の一部をこちらのページでご紹介しています。
また、最速で英語の成績を上げたい方は、当塾までご連絡ください。こちらから資料請求をお願いします。




















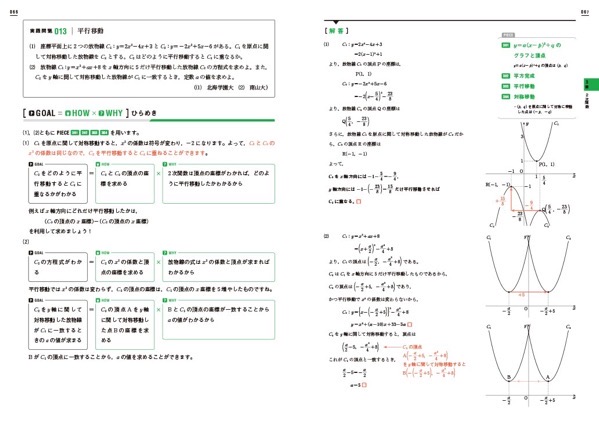







 引用:2021年慶應商学部入試
引用:2021年慶應商学部入試

