慶應義塾大学経済学部数学の完全攻略
経済学部の数学はマーク方式と記述式解答で、結果だけでなくそれに至るまでの過程を書く記述力が求められます。
問題レベルは標準的な問題が多いものの文系学部の問題としては高めです。
また、受験科目の影響と経済学がそもそも数学を使った学問のため、
理系の受験生や理系難関国公立、医学部との併願で受験する人も多数います。
高いレベルでの闘いになることは覚悟して受験に望んでいきましょう。
ページ目次
全体概観:配点150点 時間80分
例年大問は6問で、[1]~[3]は小問、[4]~[6]では記述式になっています。

- 【何からはじめたらいい?という人向け】
【まず始めることをお伝えします】 - 早慶に合格するための戦略とは?
1,2年生から合格するための戦略を立てるには? - 【高1】早慶現役合格の勉強法を徹底解説
志望校に合格するためにやるべきこと紹介 - 【高2】現役で早慶GMARCHに合格
必要な勉強法(勉強時間、参考書)を紹介 - 【高2】早慶絶対合格!!のためにすること
勉強時間、スケジュール、参考書、勉強法の紹介
慶應経済の合格最低点と目標得点
| 年度 | 配点 | 合格最低点 | 得点率 |
|---|---|---|---|
| 2023 | 420 | 248 | 59.05% |
| 2022 | 420 | 209 | 49.76% |
| 2021 | 420 | 231 | 55.00% |
| 2020 | 420 | 234 | 55.71% |
数学は難しいですが、70~80点程度は取りたいです。
![]()
出題範囲・頻出分野・難易度
出題範囲は数学ⅠAⅡB(確率分布と統計的推測を除く)となっています。
頻出分野
数列、ベクトル、図形と三角関数、微積分、指数・対数、確率
また集合・命題の分野の問題が出されており、論理的思考力を問う問題も出されています。
難易度については教科書の章末問題レベルから標準的な問題のものが出題されています。
思考力を問う問題が出されるのも特徴です。
慶應経済の数学対策
慶應義塾大学経済学部の数学の問題を解いていくにあたって、どのように考えていくのが良いのかをお伝えしていきます。
基礎問題の演習
数学力を身につけることが大事となりますが、そのためには基本的な問題が解けるようになることが重要です。
そのため、教科書に載っている問題は公式の証明まで行って下さい。
また教科書以外にも標準的な問題集の例題などを中心に解法や考え方を学ぶ必要があります。
頻出分野の問題演習
出題範囲を満遍なく勉強をすることは当然として、頻出分野は特に意欲的に問題演習をしてください。
特に数列、微積分、指数・対数、確率、べクトル、図形と方程式は得意分野にしていくようにしていきましょう。
図をやグラフを実際に書いてイメージを養うトレーニングもしていく必要があります。
記述の演習
ただ解くのではなく、途中式や導出過程、細かい条件まで含めた解答を作ってください。
基本的な問題演習をしているうちから実際の入試を意識して解答を作ることで、記述力を早いうちから身につけることができます。
特に証明問題や場合分けを要する問題では記述力が重要となります。
証明問題で論理の飛躍があったり、場合分けを書き間違うとそれだけで減点されてしまいます。
自己採点の際も、解答と照らし合わせながら細かいミスがないかどうかまで確認してください。
また、図示問題に限らず関数や平面・立体図形が登場する問題もあるので、自分で分かりやすい図を描くことが大事になります。
正確に高速で解く計算力
大問が6題で80分と、1問あたりにかけられる時間は単純計算で15分です。出題量の半分ほどがマークシートなので計算ミスが命取りになります。
そのため、迅速かつ正確な計算力が必要となります。
日ごろの問題演習で要領よく正確に計算していくとともに、より早く解ける別解やっ公式も身に着けておきましょう。
過去問を解く際には・・・
問題演習に慣れてきたら、実際に過去問に取り組みましょう。
この際、本番通りの時間で解くことが大切です。
数学ではどの分野が何問目に出るかが分からないので、時間を測って問題演習をし、自分が解きやすいと思った問題から解き始めることが重要となってきます。
あまり1つの大問を完答することにこだわりすぎるとかえって点数が下がります。
大問前半の比較的易しい問題を確実に解答することで、得点を伸ばしていきましょう。
ただし、時間内に解けなかった問題もその後に問題演習として解くことも大事です。
時間内に解けなかった問題は必然的に苦手な問題であるため、苦手をつぶす意味でも解けなかった問題の復習をしましょう。
慶應経済数学の合格する解き方とは?
2014年度 経済学部 数学
大問2(1)、(2)、(3)
(1)![]()
より
![]()
![]() で極致をもつので
で極致をもつので
![]()
問題文よりα≠βである
f(x)の解がα、βということなので解と係数の関係か
![]()
となります。![]() をそれぞれ求めると
をそれぞれ求めると
![]()
![]()
よって![]() の交点はこの式を連立すればよいので交点の座標は
の交点はこの式を連立すればよいので交点の座標は
![]()
となります。
(2)今回求める面積は下図のSです。
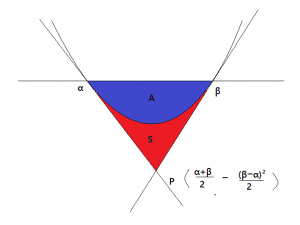
Aの部分は1/6の公式が使えます。S+Aは三角形の面積なので
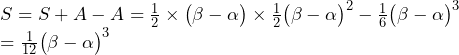
(3)(2)で求めたSをa,bを使って表します。
その際にSを基本対称式を使ってa,bを代入しやすいように変形します。
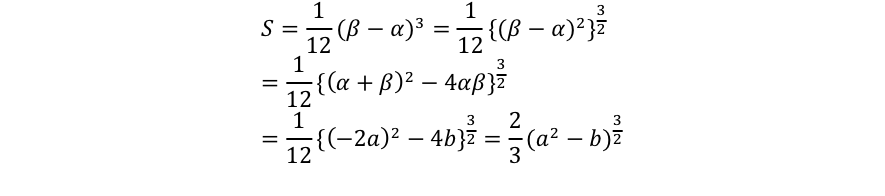
ここで![]() とおくと問題文に書いているようにa,bが変化するとab平面上で放物線
とおくと問題文に書いているようにa,bが変化するとab平面上で放物線![]() が下図の領域で共有点を持つことである。(紫:
が下図の領域で共有点を持つことである。(紫:![]() ,黄色:
,黄色:![]() ,水色:
,水色:![]() ,緑:
,緑:![]() )
)
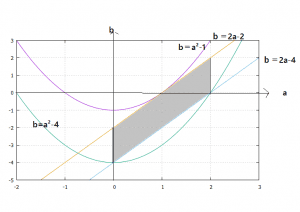
kが最大になるのは点(0,-4),(2,0)のときでk=4である。一方kが最小になるのは直線b=2a-2と接するとき、つまり
![]()
が重解を持つときなので、判別式を計算するとk=1となります。ゆえに
Sの最大値:![]()
Sの最小値:![]()
となります。
慶應義塾大学経済学部に圧倒的な実力で合格できる専門対策をします

まずは資料請求・お問い合わせ・学習相談から!
早慶専門個別指導塾HIRO ACADEMIAには、慶應義塾大学専門として経済学部への圧倒的な合格ノウハウがございます。
少しでもご興味をお持ちいただいた方は、まずは合格に役立つノウハウや情報を、詰め込んだ資料をご請求ください。
また、慶應義塾大学経済学部に合格するためにどのよう勉強をしたらよいのかを指示する学習カウンセリングも承っています。学習状況を伺った上で、残りの期間でどう受かるかを提案いたしますので、ぜひお気軽にお電話いただければと思います。
⇒ 慶應義塾大学・経済学部に合格したい方は、まずは当塾の資料をご請求ください。



















Published by