早稲田大学理工過去問徹底研究 2018年 大問5 方針の立て方 (1)と(2)は実際に簡単な図を描くことで解答を得る. (3)前問(1)と(2)で見た通り頂点の選び方で共通部分が変わる.頂点の選び方は70通りあるが,回転での対称性を考慮すれば,考えるべきパターン数はもっと減るのではと考え,一先ず虱潰
- …続きを読む
-
早稲田大学理工過去問徹底研究 2018年 大問5
方針の立て方
(1)と(2)は実際に簡単な図を描くことで解答を得る.
(3)前問(1)と(2)で見た通り頂点の選び方で共通部分が変わる.頂点の選び方は70通りあるが,回転での対称性を考慮すれば,考えるべきパターン数はもっと減るのではと考え,一先ず虱潰しで考えてみる.すると実際,考えるべきパターン数は多くならないため,数え上げる.解答例
(1)
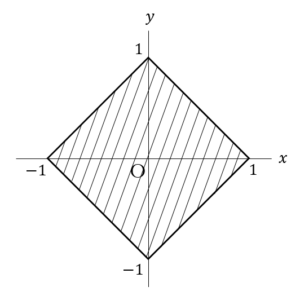
立方体の各面の中心を頂点とする立体となる.
よって,正八面体……(答)(2)
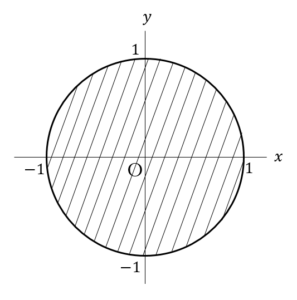
 と
と が立方体の中心で交わるのみ.
が立方体の中心で交わるのみ.
よって,点……(答)(3)
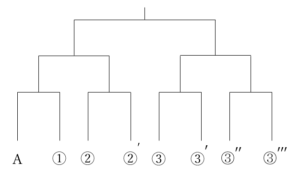
4点の頂点の選び方は,全部で 通り.
通り.
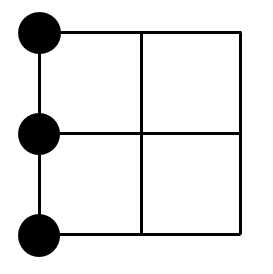
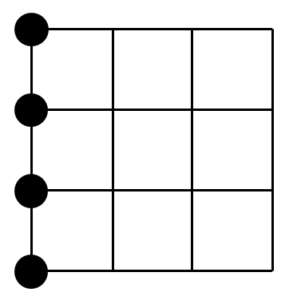
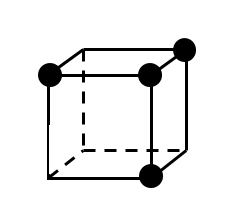
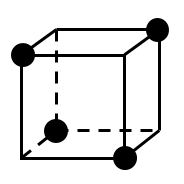
以下では,1つの面に着目(図では面 )し,その面から何個の頂点が選ばれているかで場合分けする.選ばれた頂点を●で表すことにする.
)し,その面から何個の頂点が選ばれているかで場合分けする.選ばれた頂点を●で表すことにする.
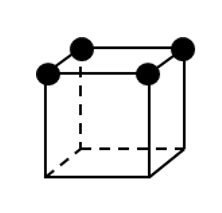
(ⅰ)4個の場合

上図のような場合,共通部分はない.
4つの●が集合する面の選び方を考えれば,回転して左図のパターンになるものは全部で6通りあることが分かる.
(ⅱ)3点の場合
(ⅱ―ⅰ)

上図のような場合,共通部分はない.
上図の のように,隣り合うすべての頂点が選ばれている点の配置を考えれば,回転して上図のパターンになるものは全部で8通りあることが分かる.
のように,隣り合うすべての頂点が選ばれている点の配置を考えれば,回転して上図のパターンになるものは全部で8通りあることが分かる.
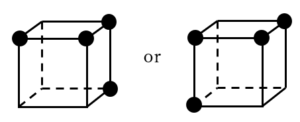
(ⅱ―ⅱ)

上図のような場合,共通部分は1点となる.
上図の or
or のような線分の配置を考えれば,回転して上図のどちらかのパターンになるものは全部で24通りあることが分かる.
のような線分の配置を考えれば,回転して上図のどちらかのパターンになるものは全部で24通りあることが分かる.
(ⅱ―ⅲ)

上図のような場合,共通部分は立体図形となる.
上図の のように,隣り合うすべての頂点が選ばれていない点の配置は8通りあり,3点が集合する面がどの配置にあるかで3通りあるため,回転して上図のパターンになるものは全部で24通りあることが分かる.
のように,隣り合うすべての頂点が選ばれていない点の配置は8通りあり,3点が集合する面がどの配置にあるかで3通りあるため,回転して上図のパターンになるものは全部で24通りあることが分かる.
(ⅲ)2点の場合
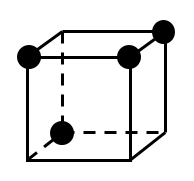
(ⅲ―ⅰ)

上図のような場合,共通部分は線分となる.
回転して上図のパターンになるものは全部で6通りある.
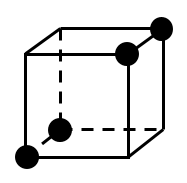
(ⅲ―ⅱ)

上図のような場合,共通部分は立体図形となる.
回転して上図のパターンになるものは全部で2通りある.
以上より,
 ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。







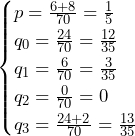 ……(答)
……(答)

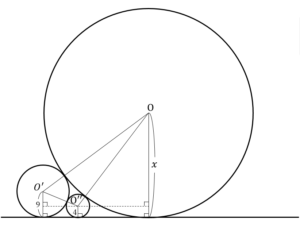

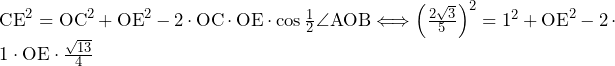
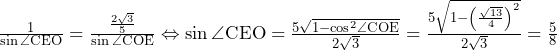
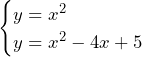
![Rendered by QuickLaTeX.com \int_{-\frac{3}{4}}^{\frac{5}{4}}\left\{x^2-\left(\frac{1}{2}x^2-\frac{3}{4}x-\frac{9}{32}\right)\right\}dx+\int_{\frac{5}{4}}^{\frac{13}{4}}\left\{\left(x^2-4x+5\right)-\left(\frac{1}{2}x^2-\frac{3}{4}x-\frac{9}{32}\right)\right\}dx=\int_{-\frac{3}{4}}^{\frac{5}{4}}\left(\frac{1}{2}x^2+\frac{3}{4}x+\frac{9}{32}\right)dx+\int_{\frac{5}{4}}^{\frac{13}{4}}\left(\frac{1}{2}x^2-\frac{13}{4}x+\frac{169}{32}\right)dx=\left[\frac{1}{6}x^3+\frac{3}{8}x^2+\frac{9}{32}x\right]_{-\frac{3}{4}}^{\frac{5}{4}}+\left[\frac{1}{6}x^3-\frac{13}{8}x^2+\frac{169}{32}x\right]_{\frac{5}{4}}^{\frac{13}{4}}=\frac{4}{3}+\frac{4}{3}=\frac{8}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-43566093742bcefede7fed31bdf18173_l3.png) ……(答)
……(答)
 ……(答)
……(答)