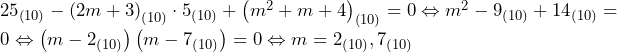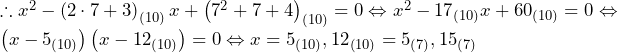方針の立て方 の範囲((31)~(34))については,が図形的にどのような意味を持つのかを考えることで解法を得る.図形と方程式の問題では,数式を図形に,或いは図形を数式に直して考えることが重要である. 長方形の面積とその最大値((35)~(56))については典型的な問題であるため,特筆事項なし. 解
- …続きを読む
- 方針の立て方
 の範囲((31)~(34))については,
の範囲((31)~(34))については, が図形的にどのような意味を持つのかを考えることで解法を得る.図形と方程式の問題では,数式を図形に,或いは図形を数式に直して考えることが重要である.
が図形的にどのような意味を持つのかを考えることで解法を得る.図形と方程式の問題では,数式を図形に,或いは図形を数式に直して考えることが重要である.
長方形 の面積とその最大値((35)~(56))については典型的な問題であるため,特筆事項なし.
の面積とその最大値((35)~(56))については典型的な問題であるため,特筆事項なし.
解答例
(31)(32)(33)(34)……
(35)(36)(37)……
(38)(39)(40)……
(41)(42)(43)……
(44)(45)(46)……
(47)(48)(49)(50)……
(51)(52)……
(53)(54)……
(55)(56)……
解説
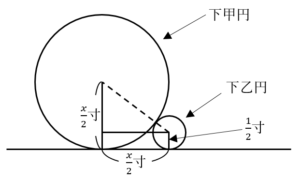
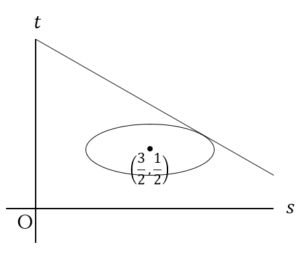
○ の範囲((31)~(34)について)
の範囲((31)~(34)について)
 は線分
は線分 の切片に当たる.線分
の切片に当たる.線分 の切片の下限は,直線
の切片の下限は,直線 が放物線
が放物線 の接線となるとき.
の接線となるとき.
 より,直線
より,直線 が放物線
が放物線 の接線となるとき,接点は
の接線となるとき,接点は となる.このとき直線
となる.このとき直線 の切片
の切片 は,
は,

 ……(答)
……(答)〇長方形
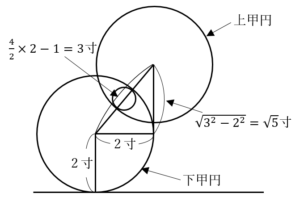
 の面積((35)~(46)について)
の面積((35)~(46)について)
 と
と の交点
の交点 ,
, の座標は,
の座標は, ,
,

線分 の長さは,線分
の長さは,線分 が直線
が直線 と直交することより,点
と直交することより,点 と直線
と直線 との距離に等しい.
との距離に等しい. より,
より, であることに注意すると,
であることに注意すると,

よって,求める面積は,
 ……(答)
……(答)〇長方形
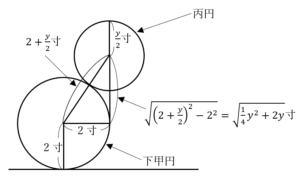
 の面積の最大値((47)~(56)について)
の面積の最大値((47)~(56)について)
 とおくと,
とおくと, となる.
となる.
増減表を描くと,

















よって,長方形
 の面積は
の面積は のときに,最大値
のときに,最大値 となる.……(答)
となる.……(答)





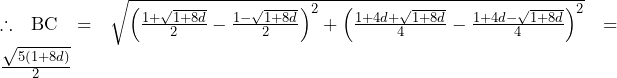
 ……(答)
……(答)

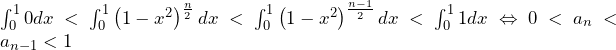
![Rendered by QuickLaTeX.com a_n=\int_{0}^{1}\left(1-x^2\right)^\frac{n}{2}dx=\int_{0}^{1}{\left(x\right)^\prime\left(1-x^2\right)^\frac{n}{2}}dx=\left[x\left(1-x^2\right)^\frac{n}{2}\right]_0^1-\int_{0}^{1}{x\cdot\frac{n}{2}\left(1-x^2\right)^\frac{n-2}{2}\cdot\left(-2x\right)}dx=n\int_{0}^{1}{x^2\left(1-x^2\right)^\frac{n-2}{2}}dx](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-3383a4e3a41de53f568ac6beddb7b89b_l3.png)
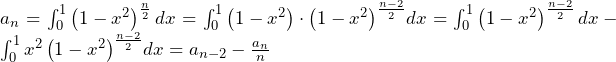
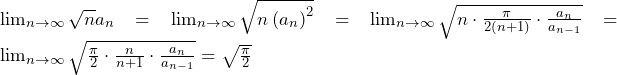 ……(答)
……(答)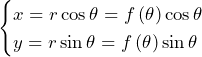
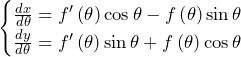
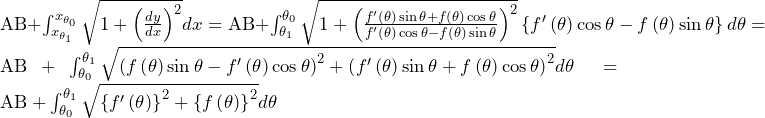
![Rendered by QuickLaTeX.com \mathrm{AB}+\int_{\theta_0}^{\theta_1}\sqrt{\left\{f^\prime\left(\theta\right)\right\}^2+\left\{f\left(\theta\right)\right\}^2}d\theta=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}\sqrt{\left\{\alpha\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2+\left\{\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2}d\theta\bigm=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}{\sqrt{1+\alpha^2}\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}}d\theta=\frac{v}{\sqrt{v^2-1}}+\sqrt{1+\alpha^2}\beta\left[\frac{1}{\alpha}e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right]_{\frac{\pi}{2}}^{\theta_1}\bigm=\frac{v}{\sqrt{v^2-1}}-\frac{\beta}{\alpha}\sqrt{1+\alpha^2}+\frac{\beta}{\alpha}\sqrt{1+\alpha^2}e^{\alpha\left(\theta_1-\frac{\pi}{2}\right)}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-3251c46fb035b1c6f3d900fd751c1cf5_l3.png)
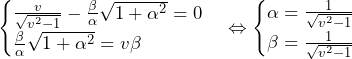 ……(答)
……(答)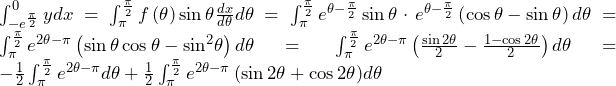
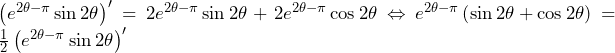
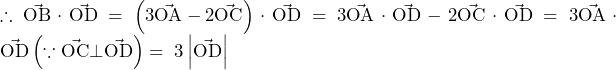 (
(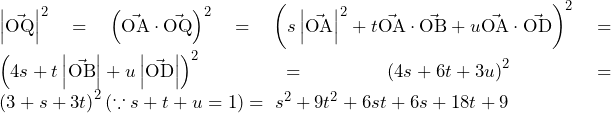
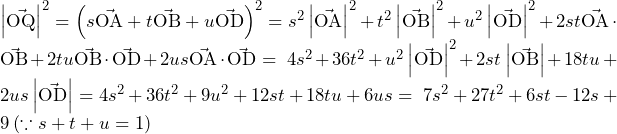
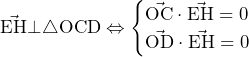
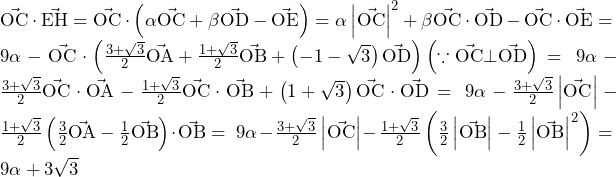
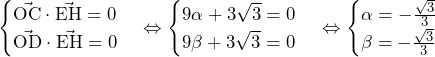
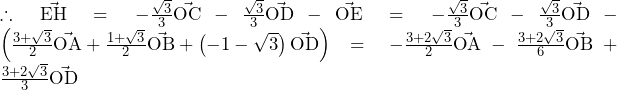
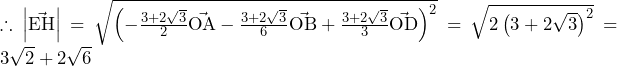

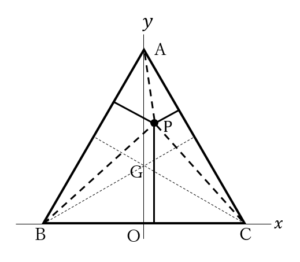
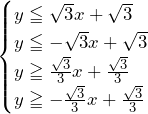
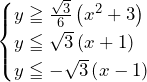
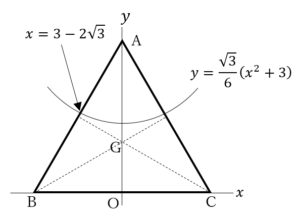
![Rendered by QuickLaTeX.com 2\int_{3-2\sqrt3}^{0}\left\{\left(\sqrt3x+\sqrt3\right)-\left(\frac{\sqrt3}{6}x^2+\frac{\sqrt3}{2}\right)\right\}dx=\left[-\frac{\sqrt3}{9}x^3+\sqrt3x^2+\sqrt3x\right]_{3-2\sqrt3}^0=16-9\sqrt3](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-ca7e2526c667d1ae7bb1ab5fab12914c_l3.png) ……(答)
……(答)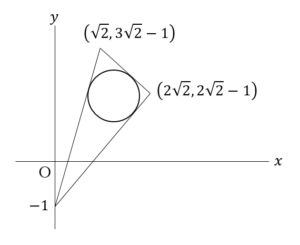
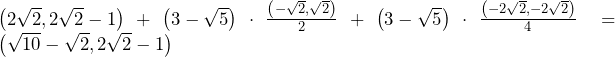 ……(答)
……(答)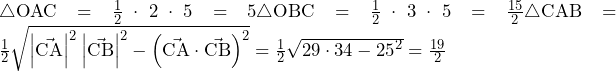 より,
より,