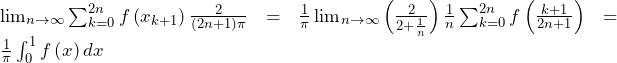早稲田大学理工過去問徹底研究 2017年 大問2 方針の立て方 (1)基本問題であるため特筆事項なし. (2)絶対値問題の初動捜査である符号の変わり目で場合分け(分割)を行う. (3)典型的な微分法の最大最小問題であり特筆事項なし. 解答例 (1) よって,増減表を描くと, また,で軸と交わる. よ
- …続きを読む
-
早稲田大学理工過去問徹底研究 2017年 大問2
方針の立て方
(1)基本問題であるため特筆事項なし.
(2)絶対値問題の初動捜査である符号の変わり目で場合分け(分割)を行う.
(3)典型的な微分法の最大最小問題であり特筆事項なし.解答例
(1)

よって,増減表を描くと,













また, で
で 軸と交わる.
軸と交わる.
よって,
 (上図が答え)
(上図が答え)(2)
 である.
である. で
で が正から負に符号変化することに注意すると,
が正から負に符号変化することに注意すると,

ここで,
 (第2項に部分積分)
(第2項に部分積分) (
( は積分定数)
は積分定数)
![Rendered by QuickLaTeX.com \therefore S=\left[\left(x-\frac{1}{a}\right)e^{-a\left(x-2\right)}\right]_0^{\frac{2}{a}}-\left[\left(x-\frac{1}{a}\right)e^{-a\left(x-2\right)}\right]_{\frac{2}{a}}^{\frac{3}{a}}=\frac{e^{2a}}{a}\left(1+2e^{-2}-2e^{-3}\right)](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAlUAAAAmAQAAAADFVFNZAAAAAnRSTlMAAHaTzTgAAAAZSURBVBgZ7cExAQAAAMIg+6deBn9gAADALQtIAAGNgPdvAAAAAElFTkSuQmCC) ……(答)
……(答)(3)
 に注意して,
に注意して, の最小値を考える.
の最小値を考える.
 とする.
とする.

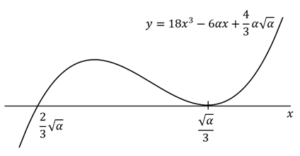
増減表を描くと,









最小 
よって,
 を最小にする
を最小にする の値は,
の値は, ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。






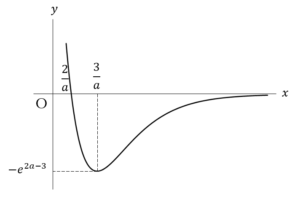 (上図が答え)
(上図が答え)
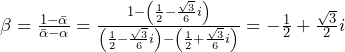 ……(答)
……(答)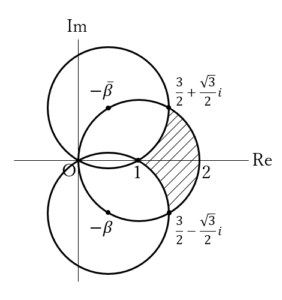
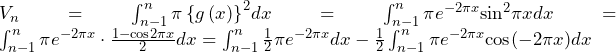
![Rendered by QuickLaTeX.com \int_{n-1}^{n}{\pi e^{-2\pi x}\cos{\left(-2\pi x\right)}}dx=-\frac{1}{2}\int_{-2\left(n-1\right)\pi}^{-2n\pi}{e^y\cos{y}}dy\bigm=-\frac{1}{2}\left[\frac{1}{2}e^y\left(\cos{y}+\sin{y}\right)\right]_{-2\left(n-1\right)\pi}^{-2n\pi}\bigm=-\frac{1}{4}\left(e^{-2n\pi}-e^{-2\left(n-1\right)\pi}\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-df13329429bcde4e2ecc7f39a38e588b_l3.png)
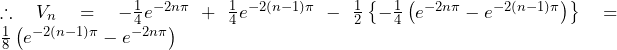 ……(答)
……(答)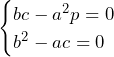
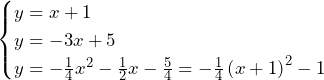
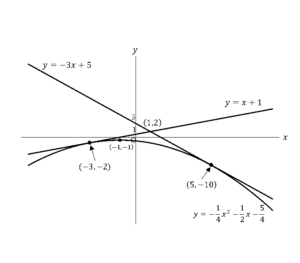
![Rendered by QuickLaTeX.com \int_{-3}^{1}\left\{\left(x+1\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx+\int_{1}^{5}\left\{\left(-3x+5\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx\bigm=\left[\frac{1}{12}x^3+\frac{3}{4}x^2+\frac{9}{4}x\right]_{-3}^1+\left[\frac{1}{12}x^3-\frac{5}{4}x^2+\frac{25}{4}x\right]_1^5=\frac{32}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-bbec6b7afbfd51917ee8a7761b2bc8b3_l3.png) ……(答)
……(答)
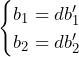 (
(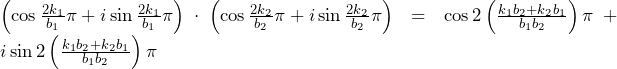
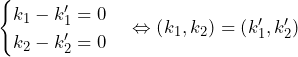
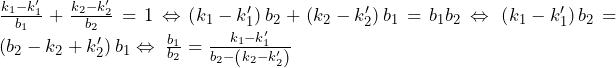
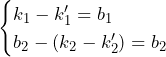
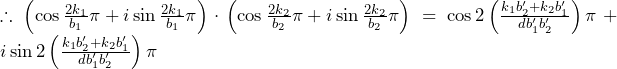
![Rendered by QuickLaTeX.com \therefore\left\{\min_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}\right\}\int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx\leqq a_k\leqq\left\{\max_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}\right\}\int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-f36be33140d882a415e9c83b4517d00d_l3.png)
![Rendered by QuickLaTeX.com \int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx=\left[-\frac{1}{\left(2n+1\right)\pi}\cos{\left(\left(2n+1\right)\pi x\right)}\right]_{x_k}^{x_{k+1}}\bigm=\frac{\left(-1\right)^k-\left(-1\right)^{k+1}}{\left(2n+1\right)\pi}\bigm=\frac{2}{\left(2n+1\right)\pi}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-c2feed9a41ae6737010103dd006acf33_l3.png) (∵
(∵