方針の立て方 (1)は積分方程式の典型問題であるため特筆事項なし. (2)は前問での議論を踏まえれば良い.が2つ出てきてしまうから,等式を満たすが2つ出てきてしまうのである.よって,が1つだけ出てくるならば,等式を満たすも1つしか出てこないと考える. (3)は,まずは積分計算を素直に行えば良い.「に
- …続きを読む
-
方針の立て方
(1)は積分方程式の典型問題であるため特筆事項なし.
(2)は前問での議論を踏まえれば良い. が2つ出てきてしまうから,等式を満たす
が2つ出てきてしまうから,等式を満たす が2つ出てきてしまうのである.よって,
が2つ出てきてしまうのである.よって, が1つだけ出てくるならば,等式を満たす
が1つだけ出てくるならば,等式を満たす も1つしか出てこないと考える.
も1つしか出てこないと考える.
(3)は,まずは積分計算を素直に行えば良い.「 によらない」という条件が考えにくいが,実際に
によらない」という条件が考えにくいが,実際に に適当な値を代入して,それらが全てイコールになると考えると,分子が0になるという結論に達する.
に適当な値を代入して,それらが全てイコールになると考えると,分子が0になるという結論に達する.
(4)計算するだけ.解答例
(1)
 (
( は定数)とおくと,
は定数)とおくと,

よって,
![Rendered by QuickLaTeX.com A=\int_{0}^{2}f\left(t\right)dt=\int_{0}^{2}\left(-3t^2+t+A^2\right)dt=\left[-t^3+\frac{1}{2}t^2+A^2t\right]_0^2=2A^2-6\Leftrightarrow2A^2-A-6=0\Leftrightarrow\left(2A+3\right)\left(A-2\right)=0](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAAAxAQAAAACpSAPMAAAAAnRSTlMAAHaTzTgAAAAYSURBVBgZ7cEBAQAAAICQ/q/uCAIAAAAGDx8AAYTy+7EAAAAASUVORK5CYII=)

これを に代入すれば,
に代入すれば,
 または
または ……(答)
……(答)(2)
 (
( は定数)とおくと,
は定数)とおくと,

よって,
![Rendered by QuickLaTeX.com A=\int_{0}^{2}f\left(t\right)dt=\int_{0}^{2}\left(\frac{3}{a}t^2-\frac{1}{a}t+A^2\right)dt=\left[\frac{1}{a}t^3-\frac{1}{2a}t^2+A^2t\right]_0^2=2A^2+\frac{6}{a}\Leftrightarrow2A^2-A+\frac{6}{a}=0](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAAA0AQAAAAD5hZJ/AAAAAnRSTlMAAHaTzTgAAAAaSURBVFjD7cEBAQAAAIIg/69uSEABAAAATwYQDAABv7z5vQAAAABJRU5ErkJggg==)
題意を満たすには, に関する二次方程式:
に関する二次方程式: の解が重解となれば必要十分.
の解が重解となれば必要十分.
よって,判別式が0であれば必要十分であるから,
 ……(答)
……(答)(3)
![Rendered by QuickLaTeX.com \int_{0}^{b}\left\{f\left(x\right)-f\left(b\right)\right\}dx=\int_{0}^{b}\left\{\frac{3}{a}x^2-\frac{1}{a}x-\frac{3}{a}b^2+\frac{1}{a}b\right\}dx=\left[\frac{1}{a}x^3-\frac{1}{2a}x^2-\frac{3}{a}b^2x+\frac{1}{a}bx\right]_0^b=-\frac{b^2\left(4b-1\right)}{2a}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmgAAAA4AQAAAABhhTk6AAAAAnRSTlMAAHaTzTgAAAAaSURBVFjD7cEBAQAAAIIg/69uSEABAAAAfBkREAABcmKxnAAAAABJRU5ErkJggg==)
よって, の値が
の値が によらない場合を考えると,分子が0となるとき.
によらない場合を考えると,分子が0となるとき. が正の実数であることから,
が正の実数であることから,
 ……(答)
……(答)(4)
 である.また,
である.また, のとき,(2)で考えた
のとき,(2)で考えた に関する二次方程式の解は,
に関する二次方程式の解は, .
.
よって,
![Rendered by QuickLaTeX.com \int_{b}^{2}f\left(x\right)dx=\int_{\frac{1}{4}}^{2}\left(\frac{1}{16}x^2-\frac{1}{48}x+\frac{1}{16}\right)dx=\frac{1}{48}\left[x^3-\frac{1}{2}x^2+3x\right]_{\frac{1}{4}}^2=\frac{721}{3072}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAioAAAAiAQAAAABZh89aAAAAAnRSTlMAAHaTzTgAAAAZSURBVEjH7cExAQAAAMKg9U9tCj+gAAD4GQluAAEMk8dvAAAAAElFTkSuQmCC) ……(答)
……(答)






![Rendered by QuickLaTeX.com A=\int_{0}^{2}f\left(t\right)dt=\int_{0}^{2}\left(\frac{3}{a}t^2-\frac{1}{a}t+A^2\right)dt=\left[\frac{1}{a}t^3-\frac{1}{2a}t^2+A^2t\right]_0^2=2A^2+\frac{6}{a}\Leftrightarrow2A^2-A+\frac{6}{a}=0](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-ab0bf548b4a46975e7979ac67d04290f_l3.png)
![Rendered by QuickLaTeX.com \int_{0}^{b}\left\{f\left(x\right)-f\left(b\right)\right\}dx=\int_{0}^{b}\left\{\frac{3}{a}x^2-\frac{1}{a}x-\frac{3}{a}b^2+\frac{1}{a}b\right\}dx=\left[\frac{1}{a}x^3-\frac{1}{2a}x^2-\frac{3}{a}b^2x+\frac{1}{a}bx\right]_0^b=-\frac{b^2\left(4b-1\right)}{2a}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a1ae218f005a4a94ff3accbf2e2f76ee_l3.png)
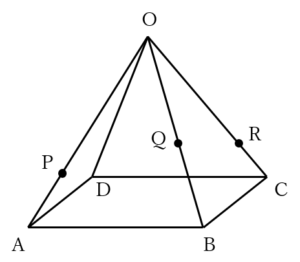
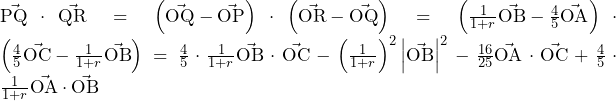
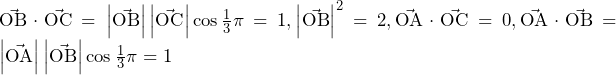 であるから,
であるから,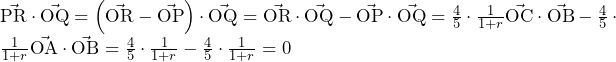 ……(答)
……(答)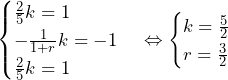
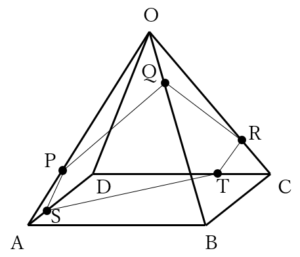
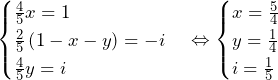
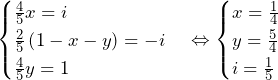
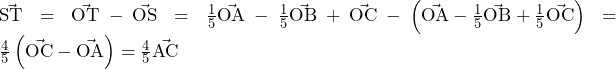
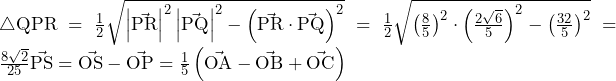 より,
より,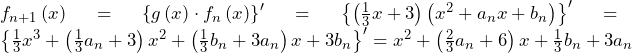
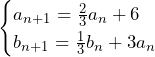 ……(答)
……(答)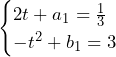
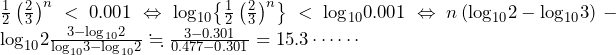
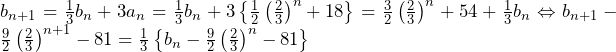
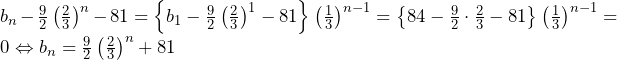 ……(答)
……(答)
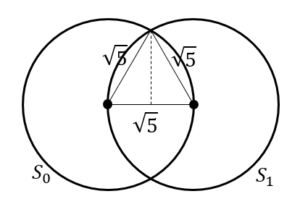
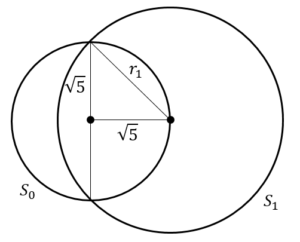
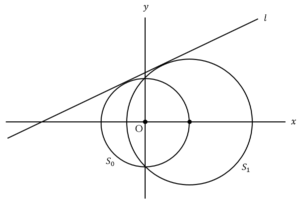
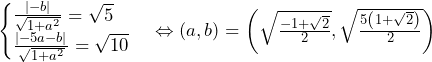
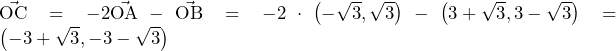
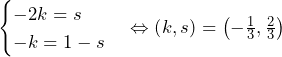
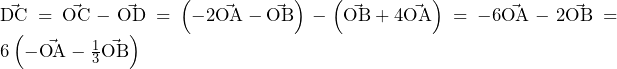
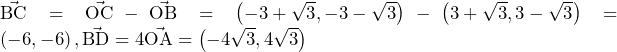 より,
より,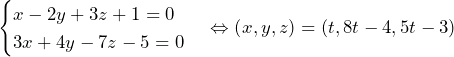
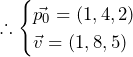 ……(答)
……(答)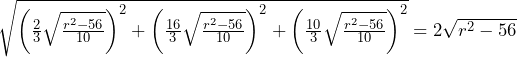
![Rendered by QuickLaTeX.com \int_{x_m}^{x_a+1}\left|m\left(x\right)-a\left(x\right)\right|dx=\int_{4}^{7}\left|x^2-8x+17-\left(\frac{1}{3}x^2-4x+17\right)\right|dx=\int_{4}^{7}\left|\frac{2}{3}x\left(x-6\right)\right|dx=\int_{4}^{6}\left\{-\frac{2}{3}x\left(x-6\right)\right\}dx+\int_{6}^{7}{\frac{2}{3}x\left(x-6\right)}dx=\left[2x^2-\frac{2}{9}x^3\right]_4^6+\left[\frac{2}{9}x^3-2x^2\right]_6^7=\frac{76}{9}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-f16c686959dba9c1141ca1d2b264f9d3_l3.png) ……(答)
……(答)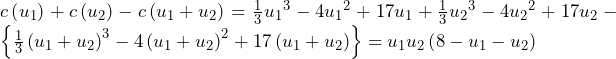 ……(答)
……(答)

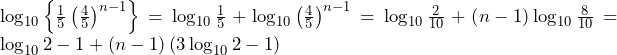
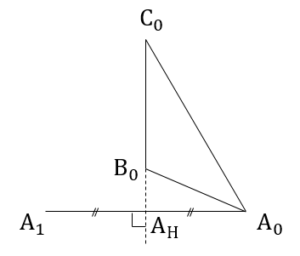
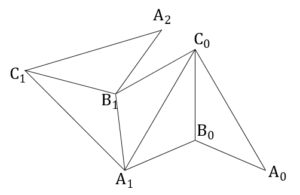
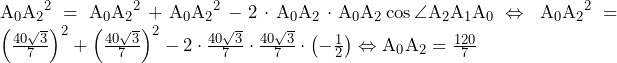 ……(答)
……(答)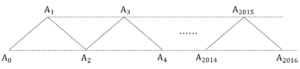
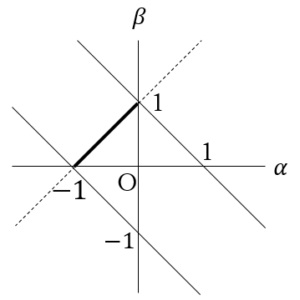
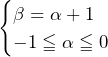
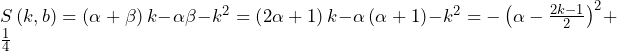
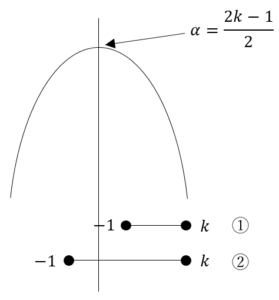
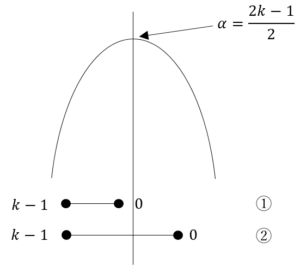
![Rendered by QuickLaTeX.com \int_{-1}^{-\frac{1}{2}}\left(-k^2-k\right)dk+\int_{-\frac{1}{2}}^{0}\frac{1}{4}dk+\int_{0}^{\frac{1}{2}}\frac{1}{4}dk+\int_{\frac{1}{2}}^{1}\left(-k^2+k\right)dk=\left[-\frac{1}{3}k^3-\frac{1}{2}k^2\right]_{-1}^{-\frac{1}{2}}+\left[\frac{1}{4}k\right]_{-\frac{1}{2}}^0+\left[\frac{1}{4}k\right]_0^{\frac{1}{2}}+\left[-\frac{1}{3}k^3+\frac{1}{2}k^2\right]_{\frac{1}{2}}^1=\frac{5}{12}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-e0c8bfe825912f02cafeb7f3d4b9999f_l3.png) ……(答)
……(答)