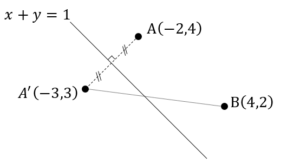
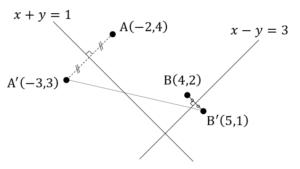
方針の立て方 (1) 典型問題であり,特筆事項なし. (2) 代数方程式の有理数解に着目していることから解法を得る. (3) 実際に考えてみることで解法を得る.ただし,を正2016角形で考えるのは難しいため,正4角形や,正5角形,正6角形などで考えてみる.そうすると,約数の問題であることに気付ける.
- …続きを読む
- 方針の立て方
(1)
典型問題であり,特筆事項なし.(2)
代数方程式の有理数解に着目していることから解法を得る.(3)
実際に考えてみることで解法を得る.ただし, を正2016角形で考えるのは難しいため,正4角形や,正5角形,正6角形などで考えてみる.そうすると,約数の問題であることに気付ける.
を正2016角形で考えるのは難しいため,正4角形や,正5角形,正6角形などで考えてみる.そうすると,約数の問題であることに気付ける.(4)
最初の式のままでは考えづらいため,変形を試みる.そこで,積和の公式を使って,三角関数の積の形を和の形に直す.
本問に限らず,数学では,和から積への変形,積から和への変形をすることで解法が見えることが多いため,困ったときにはこのような変形をとりあえず試みることを心がけよう.解答例
(1)ア:
(2)イ:
(3)ウ:
(4)エ:
解説
(1)
合同式の法は全部2016とする.

である.
 ……(答)
……(答)(2)
有理数解は全て

の形で表せる.よって,1以上の有理数解の候補は, である.
である.
(ⅰ) が解になると仮定して,方程式に代入すると
が解になると仮定して,方程式に代入すると

(ⅱ) が解になると仮定して,方程式に代入すると
が解になると仮定して,方程式に代入すると

(ⅱ) が解になると仮定して,方程式に代入すると
が解になると仮定して,方程式に代入すると

以上(ⅰ)~(ⅲ)より,求める の最小値は,5……(答)
の最小値は,5……(答)(3)
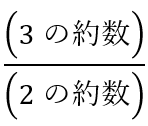
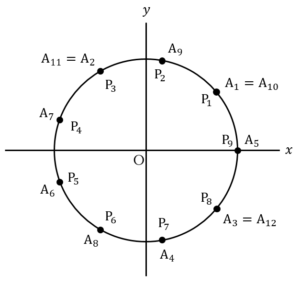
2016の任意の約数を とする.
とする.
 の頂点を結ぶことで作ることができる正多角形は,正
の頂点を結ぶことで作ることができる正多角形は,正 角形(
角形( を除く)のみである.
を除く)のみである.
正 角形の作り方は
角形の作り方は 通りあるが,
通りあるが, も2016の約数となる.
も2016の約数となる.
よって,求める個数は,2016の約数の和から, のときの分
のときの分 を除いた個数となる.
を除いた個数となる. より,2016の約数の和は,
より,2016の約数の和は,

よって,求める個数は,
 個……(答)
個……(答)(4)

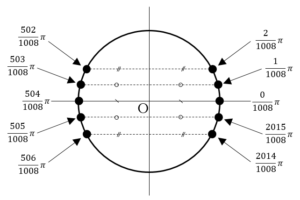
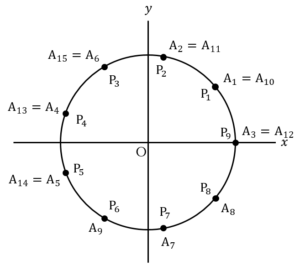
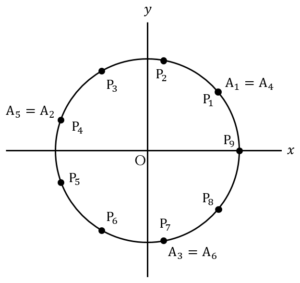
ここで,積和の公式より,

であるから,

 とおくと,
とおくと,

上図のように,単位円上では左右対称であるため,項が全て相殺し,0となる.

よって,
 ……(答)
……(答)






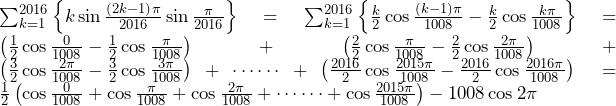

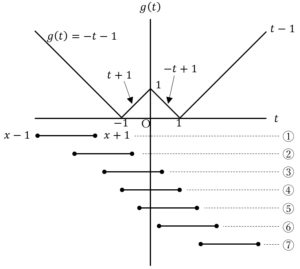
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{-1}\left(-t-1\right)dt+\frac{1}{2}\int_{-1}^{x+1}\left(t+1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2-t\right]_{x-1}^{-1}+\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{-1}^{x+1}=\frac{1}{2}\left(x^2+2x+2\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-39f866a3cf0aa6d994ba926375844cd8_l3.png)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{-1}\left(-t-1\right)dt+\frac{1}{2}\int_{-1}^{0}\left(t+1\right)dt+\frac{1}{2}\int_{0}^{x+1}\left(-t+1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2-t\right]_{x-1}^{-1}+\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{-1}^0+\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_0^{x+1}=\frac{1}{2}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-6432dfc95b1fd3fc8ab0566581f9478a_l3.png)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{0}\left(t+1\right)dt+\frac{1}{2}\int_{0}^{1}\left(-t+1\right)dt+\frac{1}{2}\int_{1}^{x+1}\left(t-1\right)dt=\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{x-1}^0+\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_0^1+\frac{1}{2}\left[\frac{1}{2}t^2-t\right]_1^{x+1}=\frac{1}{2}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-b5cfbd01a7849bbc24254319f21aa456_l3.png)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{1}\left(-t+1\right)dt+\frac{1}{2}\int_{1}^{x+1}\left(t-1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_{x-1}^1+\frac{1}{2}\left[\frac{1}{2}t^2-t\right]_1^{x+1}=\frac{1}{2}\left(x^2-2x+2\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-02980b127b2365339e8eef20ba5c599a_l3.png)
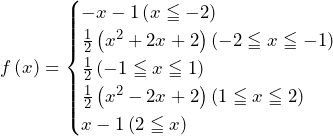
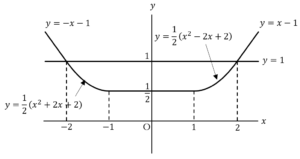
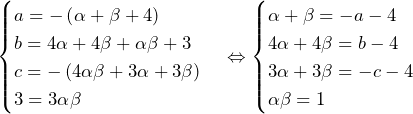
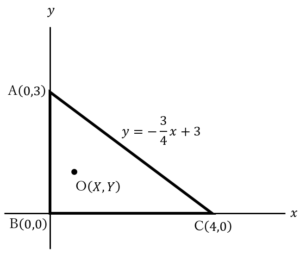
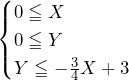 ……(*)
……(*)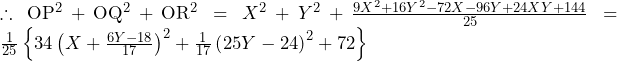
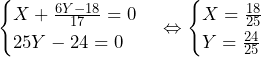 で
で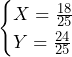 は(*)を満たす.
は(*)を満たす.

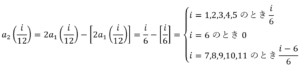
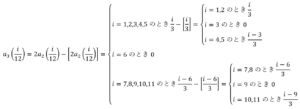
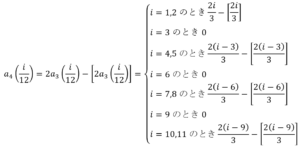
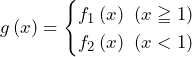
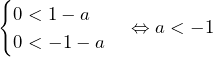 のとき
のとき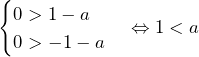 のとき
のとき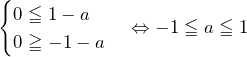 のとき
のとき
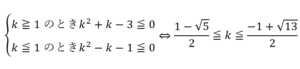
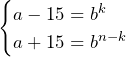
![Rendered by QuickLaTeX.com \int_{0}^{x}\left\{P\left(t\right)\right\}^mdt=\int_{0}^{x}\left\{at+b\right\}^2dt=\left[\frac{1}{3}a^2t^3+abt^2+b^2t\right]_0^x=\frac{1}{3}a^2x^3+abx^2+b^2x P\left(x^3\right)-P\left(0\right)=\left(ax^3+b\right)-b=ax^3](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a11b033768caae58621300cc339f8d26_l3.png)
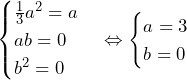
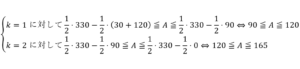
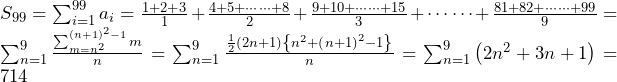 ……(答)
……(答)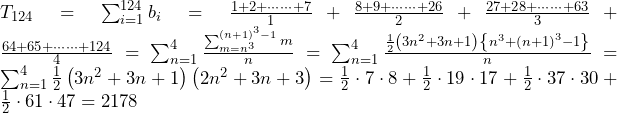 ……(答)
……(答)