早稲田大学理工学部の数学の対策
このブログでは、早稲田大学理工学部の数学に関する入試対策(出題傾向と勉強法)をご紹介していきます。
基礎知識0の状態から合格するためには何をどのようにしたら良いのかを参考書の使い方まで徹底解説!
[toc]
早稲田理工の配点
外国語:120/360点 時間90分
数学:120/360点
理科(2科目):120/360点 各60点
[su_box title="早稲田大学理工学部 科目別対策" radius="1"]▶英語対策 ▶数学対策 ▶化学対策 ▶物理対策 ▶生物対策
[/su_box]
早稲田大学理工学部の問題形式
大問は5題で、それぞれ小問に分かれています。前の小問の結果をふまえて次の小問を解くことが多く、小問同士を結びつける論理力が必要となっています。
理工学部の数学は原則すべて記述式解答で、結果だけでなくそれに至るまでの過程を書く記述力が求められます。全て解き切るのは時間的に厳しいので、部分的にでも確実に答えられる問題を探して解いていくことが大切になります。
早稲田大学理工学部頻出分野
微積は毎年のように出題され、場合の数・確率、数列は隔年で出されています。
また近年整数の出題も増えているので注意が必要です。
簡単な年は典型問題が並びますが、難しい年になるとなかなか骨のある問題が並びます
<微積>2017年度の大問2は簡単でしたが、2016年度の大問5は2016年度のセットのなかでは一番難しく、絶対取るべきかどうかというのは判断しにくいです。
しかし、誘導が丁寧なので難しくても(2)くらいまでは解き、半答は取りたいところです。
難しそうだからといって避けずに、解けるところまで粘ってみましょう。
<場合の数・確率>数列と隔年で出題されていますが、さほど難しくないですし、特徴があるわけではないので、神経質になって対策する必要はありません。n絡みの確率は漸化式、Σ、反復試行など多岐に渡りますから柔軟に対応できるようにしておくと本番も落ち着いて試験に挑めると思います。
<立体>2016、2017と二年連続で立体図形が出題されていて、来年度以降も大問で出る可能性は十分にあります。
空間は苦手にしている人が多く、差がつきやすいため難関大では好まれます。
空間は座標で押すorベクトルで攻めるの2つが大まかな方針ですから適宜図形的考察を加えたり、適切な断面で平面に落とし込んだりして、誘導をうまく汲み取って解答していきましょう。
<複素平面>こちらも課程が変わった年から連続して出題され、対策が必要不可欠な分野でしょう。難関大では複素平面の人気が高く、ほとんどの大学で出題されています。そのため他大学を受けるにおいても複素平面の学習はプラスに働くこと間違いなしでしょう。
早稲田理工の数学のための勉強法
どのようにしたら、早稲田理工学部の数学を解くことができるレベルに達するのかを具体的におつたえしていきます。そもそもの数学力が足りない人は、こちらの数学の勉強法概論をまずは読んだ方が良いでしょう。
[nlink url="https://hiroacademia.jpn.com/blog/program/rikeisugaku-benkyo/"]
典型問題を確実に解くことのできる練習を!
易の年、難の年があるものの、大問5つのなかで見たことあるな〜という問題が2つくらいはあります。
難の年は実質簡単な問題が解けるかどうかで数学で差がつくので、巷に出回っている問題集の典型的なレベルは確実に解けるようにしておきましょう。
過去問演習する際、簡単な年なら3完2半、難しい年なら2完3半を最低ラインに据えると良いでしょう。
自分なりの作戦を!
大問が5題で120分であるので、1問あたりにかけられる時間は単純計算で24分です。
問題を解く際に計算に必要な時間は多いため、落ち着いて計算を進めましょう。
検算は必ず行い、計算ミスは確実に防ぎましょう。
簡単な問題は15分程度で終わらせて、少し難し目の問題に傾斜的に時間を掛けるなど臨機応変に対応しましょう。
問題が始まったらまず全体を俯瞰して自分なりの作戦を立ててから解き始めると、大きな失敗は免れますし、良い流れに乗れるのでオススメです!
記述力をつける
ただ解くのではなく、途中式や導出過程、細かい条件まで含めた解答を作りましょう。
基本的な問題演習をしているうちから実際の入試を意識して解答を作ることで、記述力を早いうちから身につけることができます。
特に証明問題や場合分けを要する問題では記述力が重要となります。
証明問題で論理の飛躍があったり、場合分けを書き間違うとそれだけで減点されてしまいます。
自己採点の際も、解答と照らし合わせながら細かいミスがないかどうかまで確認しましょう。
また、図示問題に限らず関数や平面・立体図形が登場する問題もあるので、自分で分かりやすい図を描くことが大事になります。
計算力をつける
大問が5題で120分であるので、1問あたりにかけられる時間は単純計算で24分です。
問題を解く際に計算に必要な時間は多いため、迅速かつ正確な計算力が必要となります。
積分計算などはかなり時間を要することが多いため、繰り返し練習することで計算力を身につけましょう。
実際の問題に慣れる
問題演習に慣れてきたら、実際に過去問に取り組みましょう。この際、本番通りの時間で解くことが大切です。数学ではどの分野が何問目に出るかが分からないので、時間を測って問題演習をし、自分が解きやすいと思った問題から解き始めることが重要です。
また、先述の通り大問1問あたりにかけられる時間は24分と限られているので、あまり1つの大問を完答することにこだわりすぎるとかえって点数が下がってしまいます。
大問前半の比較的問題を確実に解答することで、得点を伸ばしていきましょう。
ただし、時間内に解けなかった問題もその後に問題演習として解くことも大事です。時間内に解けなかった問題は必然的に苦手な問題であるため、苦手をつぶす意味でも解けなかった問題の復習をしましょう。
早稲田理工過去問解説(随時更新)
圧勝している人はこう考える!
実際に問題を見て、問題を解くことができる人はどのように考えているのかを確認してください。できない人は上記の法則を利用することができていません。実際に過去問を用意して考えてみましょう。2016年度 理工学部 数学 大問Ⅱからの出題です。
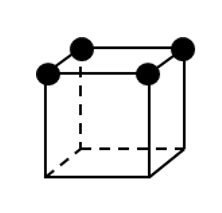
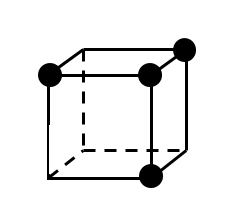
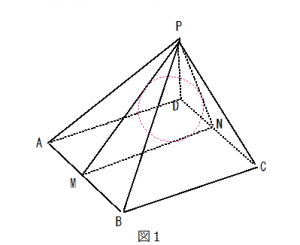
正四角錐と、それに内接する球という立体図形の問題です。
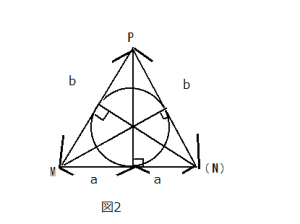
(1)立体図形のままだと分かりにくいので、断面図を描きましょう。(図1:全体図、図2:断面図)


このような断面図にすると、内接する球の半径は、二等辺三角形△PMNに内接する円の半径と同じであることがわかります(Nは線分CDの中点)。ここで、直線と円の接点において、接点と円の中心を結ぶ線分は直線に垂直になります。よって、球の半径をrとすると、△PMNの面積は

で表されます。また、△PMNはMNを底辺とする二等辺三角形であるので、MNを底辺とした時、高さは

になります。よって、△PMNの面積は

のようになります。この二通りで表された△PMNの面積は等しいので、

の式が成り立ちます。よって、球の半径は

で表されます。
(2)球の表面積は、半径をrとすると で表されます。また、正四角錐PABCDの表面積は、△PAB+△PBC+△PCD+△PDA+正方形ABCDの面積で表わされるので、
で表されます。また、正四角錐PABCDの表面積は、△PAB+△PBC+△PCD+△PDA+正方形ABCDの面積で表わされるので、

のようになります。よって、求める式は

のようになります。
(3)(2)の式が最大値をとるとき、 とすると、
とすると、

のようになります。このとき、 のときのxの値はx=3となります。よって、このときの正四角錐PABCDの体積は
のときのxの値はx=3となります。よって、このときの正四角錐PABCDの体積は

のようになります。
早稲田大学理工学部に圧倒的な実力で合格できる専門対策をします
まずは資料請求・お問い合わせ・学習相談から!
早慶専門個別指導塾HIRO ACADEMIAには、早稲田大学専門として理工学部への圧倒的な合格ノウハウがございます。
少しでもご興味をお持ちいただいた方は、まずは合格に役立つノウハウや情報を、詰め込んだ資料をご請求ください。
また、早稲田大学理工学部に合格するためにどのよう勉強をしたらよいのかを指示する学習カウンセリングも承っています。学習状況を伺った上で、残りの期間でどう受かるかを提案いたしますので、ぜひお気軽にお電話いただければと思います。
⇒ 早稲田大学理工学部に合格したい方は、まずは当塾の資料をご請求ください。
 の形に近づけることを考える.変数変換をした際には変換後の文字の範囲に気を付けよう.
の形に近づけることを考える.変数変換をした際には変換後の文字の範囲に気を付けよう.














 か
か のどちらかで最小値となる.
のどちらかで最小値となる. を代入すると,
を代入すると, であり,
であり, を代入すると,
を代入すると, であるから,答えは,
であるから,答えは, ……(答)
……(答) とおく.
とおく. が実数のため,
が実数のため, の判別式は非負である.
の判別式は非負である.
 の箇所を
の箇所を としたものとして考えられる.線形計画法で考えれば,
としたものとして考えられる.線形計画法で考えれば, が小さいときには,最小値は
が小さいときには,最小値は でとり,値を大きくするとある
でとり,値を大きくするとある で,最小値は
で,最小値は と
と の両方でとり,それより
の両方でとり,それより の値が大きくなると,最小値は
の値が大きくなると,最小値は でとる.
でとる. と
と の両方で最小値となるのは,
の両方で最小値となるのは, が成立するときであり,これを解くと,
が成立するときであり,これを解くと, より,
より, である.
である. の場合,
の場合, のとき,
のとき, ……(答)
……(答) の場合,
の場合, または,
または, のとき,
のとき, ……(答)
……(答) の場合,
の場合, のとき,
のとき, ……(答)
……(答)






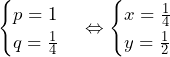 でとり,値を大きくするとある
でとり,値を大きくするとある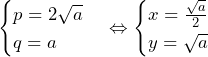 の両方でとり,それより
の両方でとり,それより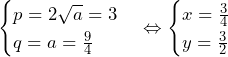 のとき,
のとき,




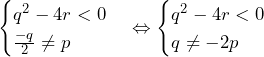 ……(答)
……(答)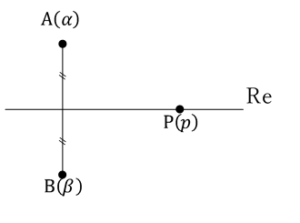
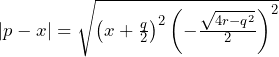
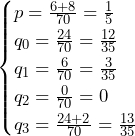 ……(答)
……(答)
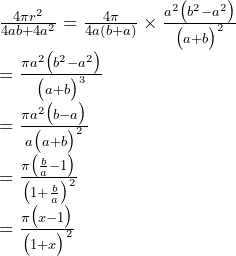
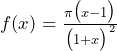 とすると、
とすると、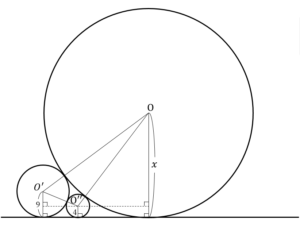

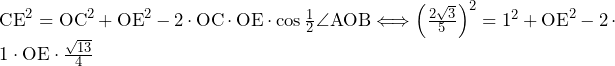
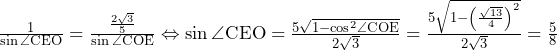
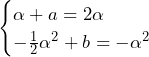
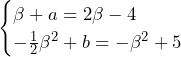
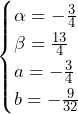
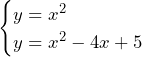
![Rendered by QuickLaTeX.com \int_{-\frac{3}{4}}^{\frac{5}{4}}\left\{x^2-\left(\frac{1}{2}x^2-\frac{3}{4}x-\frac{9}{32}\right)\right\}dx+\int_{\frac{5}{4}}^{\frac{13}{4}}\left\{\left(x^2-4x+5\right)-\left(\frac{1}{2}x^2-\frac{3}{4}x-\frac{9}{32}\right)\right\}dx=\int_{-\frac{3}{4}}^{\frac{5}{4}}\left(\frac{1}{2}x^2+\frac{3}{4}x+\frac{9}{32}\right)dx+\int_{\frac{5}{4}}^{\frac{13}{4}}\left(\frac{1}{2}x^2-\frac{13}{4}x+\frac{169}{32}\right)dx=\left[\frac{1}{6}x^3+\frac{3}{8}x^2+\frac{9}{32}x\right]_{-\frac{3}{4}}^{\frac{5}{4}}+\left[\frac{1}{6}x^3-\frac{13}{8}x^2+\frac{169}{32}x\right]_{\frac{5}{4}}^{\frac{13}{4}}=\frac{4}{3}+\frac{4}{3}=\frac{8}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-43566093742bcefede7fed31bdf18173_l3.png) ……(答)
……(答)