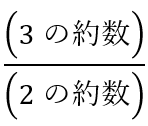
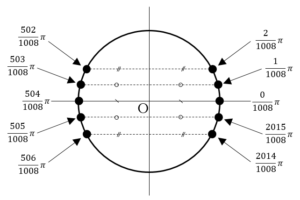
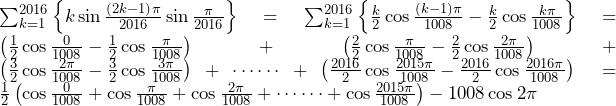文系数学勉強法応用編(アウトプット)
[speech_bubble type="ln-flat" subtype="L1" icon="seitom1.gif" name=""]どういう公式があるかわかったからあとはアウトプットすればいいだけですよ。[/speech_bubble]
上記で数学で各分野の概念を正しく理解して、高速化ができたのであれば入試レベルの問題集や過去問をやっていきましょう。1対1対応までをしっかり理解できているのであれば、早慶や医学部の問題であっても合格点を取ることができます。
そのため、現役生などで時間に余裕がなく理科科目や英語がまだ完成していないようであれば、問題集はしないで過去問と『1対1対応の数学』を繰り返しましょう。
1対1対応の数学に出題される問題は基本的に理解できていて他に教材を必要とする場合は『やさしい理系数学』をやってみると良いでしょう。
▶『やさしい理系数学』の詳しい使い方はこちらから
下記、こうしたアウトプット教材を行う上で気をつける点をご紹介していきます。
「難しい・・わからない!」と感じたら・・・
難しすぎてわからない場合は、上記で紹介した『元気が出る数学』や、『1対1対応の数学』に戻って考えてみましょう。できない問題を考え抜くというのは確かに数学的な思考力をつける上では大事です。ですが、独学で勉強していて、上述のインプット用の参考書は理解していないけど、、すべての問題の答えを覚えてしまったというレベルまで行ってしまったという場合、本人はできているつもりで次の教材に進んでしまいます。ですが、本質的な部分を理解していない!という場合も往々にあります。難しい問題にあたった場合にそういった大事なことが理解できてないということが顕著にわかるでしょう。
基礎的な参考書と応用の参考書を行ったり来たりすることで、「何だこの問題はこういうことをいいたかったのか!」と理解できるようになってきます。
もちろん、何が原因でできてないのか?当塾のようなプロの力を借りて高速で勉強するのもありでしょう。カウンセリングはこちらから行っています。
何をしているのか?を意識する
[speech_bubble type="ln-flat" subtype="L1" icon="seitom1.gif" name=""]よくわからないけど適当に公式を入れて、展開したら、答えがいつもでます。[/speech_bubble]
[speech_bubble type="ln-flat" subtype="R1" icon="platon1.jpg" name="プラトン先生"]そんな方法で勉強しても一生成績は上がりませんよ![/speech_bubble]
独学をしている人にありがちですが、よくわからないけど式の展開をした、わからないけど因数分解をしたという無意識で計算をしてしまう人がよくいます。
こういった生徒に対して、「なぜこの計算をしたのか?」と聞いても、「学校で習ったから〜、」「参考書に書いてあったから〜」と自分ではなぜなぜこの展開をしなければいけないのか理解できていません。
このような場合では数学はできるようになりません。常に式の最終形がどのような形になるのか?、目標に到達するためには何をしたら良いのか?、目的意識を式の展開をしていってください。
公式を何でもかんでも使ってみるという思考の人はいつまでたっても数学はできるようになりません。
センター試験数学
センター試験数学についてですが、センター試験の受ける目的や2次試験でも数学を使用するかどうかによって重要度が変わってきます。ここでは早慶志望の学生(文系、理系)、医学部再受験生がどのように対処したらよいのかということを確認していきます。
■早慶志望の学生でセンター試験を受ける場合
早慶志望の学生にも文系と理系と2パターン考えられますが、基本的に戦略は同じです。早慶を受ける学生ならば文理関係なく入試レベルの問題であれば、センター試験レベルの問題であれば問題なく解けるはずです。ただ、センター試験の問題形式、制限時間は特殊なので解いておく必要があるでしょう。理系の場合は過去問だけを行っていると、数学1A2Bだけの問題を解く頻度が減ってくる可能性があります。過去問を何年か分は行って慣れておくと良いでしょう。ただ、早慶志望の場合はセンター試験はそこまで大事ではないので、対策をしている時間がないという生徒は行わなくても問題ありません。
■医学部再受験生で9割以上センター試験の点数が欲しい場合
センター試験問題特有の誘導形式、短い時間内に問題を解いていくことはいくら普段演習している問題よりも簡単だとはいえ、また違った対策をしていく必要があるでしょう。計算が煩雑になるので、数学が得意!という人であっても満点を取るのは、対策をしなければ容易では無いでしょう。当塾ではセンター試験で圧勝する数学対策も行っていますので、ご連絡ください。
早慶の過去問について
早慶の過去問についてですが、過去問を行う際には点数に一喜一憂するのではなく、できないことを発見しながら課題意識を持ってっていきましょう。問題ができた際には、何故できたのか?、自身が考えた解法ではどうして問題にたどり着くことができないのか?という点を考えていく必要があります。具体的な早慶の過去問対策は以下から御覧ください。
また当塾ではどのようにしたら、早慶の過去問を解いたらよいのか?という点も徹底的に指導しています。こちらまでご連絡ください。
Q&A
ここでは入試レベルの数学の問題について当塾に寄せられる質問をQ&A形式でお答えします。
解答はプラトン先生にお答えいただきます。
[speech_bubble type="ln-flat" subtype="L1" icon="seitow3.gif" name="質問1"]数学の過去問を見てみた時に全く解くことができませんでした。やはり、問題を解くにはセンスが必要なのでしょうか?[/speech_bubble]
[speech_bubble type="ln-flat" subtype="R1" icon="platon1.jpg" name="プラトン先生"]数学の問題を解くのにセンスは必要ありません。問題を解くことができなかったのは何が原因でしょうか?まずはそれを考えてみましょう。問題文を理解することができない場合は、問題を解く上でのそもそもの前提知識が足りてない可能性があります。この場合はまずは、該当分野の概念の定義の確認、公式の証明を行ってみましょう。[/speech_bubble]
[speech_bubble type="ln-flat" subtype="L1" icon="seitom2.gif" name="質問2"]高2の段階で過去問を見てみました。正直できるようになる気がしないのですが、、これは1年でなんとかなるものなのでしょうか?[/speech_bubble]
[speech_bubble type="ln-flat" subtype="R1" icon="platon1.jpg" name="プラトン先生"]なんとかなります。2年生の段階で完璧に理解できていたらその時点で、受験勉強は完了でしょう。心配しなくても大丈夫です。問題演習をしていくうちに自身の何が足りないのか?できるようにしたらよいのか?という点には気づくことができます。頑張っていきましょう。[/speech_bubble]
合格までのスケジュール例を見てみよう!
現状と入試までの期間を踏まえてスケジュールを立ててみましょう。当塾のこれまでの相談を元に2パターンのスケジュール例をご紹介いたします。
*あくまで一例です。
【超理想的!】高2春から始めるパターン
■<高2>4月上旬 〜 7月上旬(夏休み)
中学数学の復習
■<高2>8月上旬 〜 8月下旬
坂田アキラの看護医療数学1Aが面白いほどわかる本
合格る計算1A2B
数学1Aの概念を徹底的に学び直して高速化を行う。
■<高2>9月上旬 〜 10月下旬
坂田アキラの看護医療数学1Aが面白いほどわかる本の復習
『数学2Bが面白いほどわかる本』を始める
合格る計算
■<高2>11月上旬 〜 12月下旬
坂田アキラの看護医療数学1Aが面白いほどわかる本の復習
『数学2Bが面白いほどわかる本』を始める
合格る計算
■<高2>1月上旬 〜 3月下旬
数学1A標準問題精講を行う
マセマ合格2Bを行う
■<高3>4月上旬〜5月下旬
数学1A標準問題精講復習
マセマ合格2Bの復習
坂田アキラの数学3の微分積分が面白いほどわかる本
合格る計算Ⅲを行う
■<高3>6月上旬〜7月下旬
1対1対応の数学を始める
合格る計算Ⅲ復習
■<高3>夏休み中
過去問を開始する
1対1対応の数学を復習
■<高3>8月後半以降
過去問を解きながら、それぞれの学部の対策を行っていく
【理想的!】高2夏から始めるパターン
■<高2>7月後半 〜 8月上旬
元気が出る数学を始める
合格る計算を始める
■<高2>8月上旬 〜 8月下旬
元気が出る数学の復習
合格る計算の復習
■<高2>9月上旬 〜 10月下旬
『坂田アキラの数学3の微分積分が面白いほどわかる本』を読み始める
合格る計算Ⅲを始める
■<高2>11月上旬 〜 12月下旬
『文系の数学を』始める
『坂田アキラの数学3の微分積分が面白いほどわかる本』を復習
合格る計算Ⅲ
■<高2>1月上旬 〜 3月下旬
『数学1A 標準問題精講』を始める
『マセマ合格シリーズ』を始める
合格る計算1A2BⅢ
センター試験を解いてみる 目標 140~160点
■<高3>4月上旬〜5月下旬
『数学1A 標準問題精講』を復習
『マセマ合格シリーズ』を復習
合格る計算1A2BⅢ
■<高3>6月上旬〜7月下旬
『1対1対応の数学』を始める
■<高3>夏休み中
『1対1対応の数学』の復習
早稲田、慶應大学の過去問を解いてみる この段階で5,6割が目安
■<高3>8月半以降
『1対1対応の数学』の復習
過去問を解きながら、それぞれの学部の対策を行っていく
高3から始めたい
受験期間までに1年もない場合は個別にカリキュラムを作成して対応いたします。
カウンセリングはこちらから行っております。
大雑把にスケジュールをあげてみました。特に高2からはじめるスケジュールは簡単そうに見えて実はとても大変です。それまで持っている力によっても違いますし、他の科目とのバランスも考えながら進めなければなりません。
当塾では、それぞれの生徒さんの実情に合わせてスケジュールを組んでまいります。ぜひ、ご利用ください。
必要参考書一覧
当塾で使用する参考書の一覧です。生徒の学力に応じてピックアップしていきます。
*もちろん、すべての参考書を使用するわけではありません。
クリックすると参考書の詳細ページに飛ぶことができます。
■中学数学レベル (偏差値 測定不能)
『0からやりなおす中学数学の計算問題』
『中学数学の解き方をひとつひとつわかりやすく』
■高校数学初級レベル (偏差値 30~40レベル)
『合格る計算1A/2B 合格る計算3』
『坂田アキラの 医療看護系入試数学I・Aが面白いほどわかる本』
『数学II・Bの点数が面白いほどとれる本』
『坂田アキラの数Ⅲの微分積分が面白いほど分かる本』
『スバラシク強くなると評判の元気が出る数学1A2B』
■MARCHレベル (偏差値 50~60レベル)
『文系の数学 重要事項完全習得編』
『数学I・A 標準問題精講』
『スバラシクよくわかると評判の合格!数学2・B』
■早慶レベル (偏差値 60~65レベル)
『1対1対応の演習1』『1対1対応の演習A』『1対1対応の演習2』『1対1対応の演習B』
■早慶合格レベル (偏差値 65〜レベル)
『文系数学の良問プラチカ 数学1・A・2・B』
■分野別参考書
『合格る確率』
『整数問題が面白いほどとける本』
『解法の探求・確率』















 ……(答)
……(答) .
. .
. ……(答)
……(答) に該当するのは,「1回目の操作で玉1,2回目の操作で玉2を袋Bに入れる」という事象と「1回目の操作で玉2,2回目の操作で玉1を袋Bに入れる」という事象.
に該当するのは,「1回目の操作で玉1,2回目の操作で玉2を袋Bに入れる」という事象と「1回目の操作で玉2,2回目の操作で玉1を袋Bに入れる」という事象. ,「1回目の操作で玉2,2回目の操作で玉1を袋Bに入れる」という事象が起こる確率は
,「1回目の操作で玉2,2回目の操作で玉1を袋Bに入れる」という事象が起こる確率は .
. ……(答)
……(答) ……(答)
……(答) ……(答)
……(答) ……(答)
……(答) ……(答)
……(答) であるものは,
であるものは, と
と の2個……(答)
の2個……(答) であるものは,
であるものは, と
と と
と と
と と
と と
と と
と と
と の8個……(答)
の8個……(答) であるものは,
であるものは, の1個……(答)
の1個……(答) であるものは,
であるものは, と
と と
と と
と の4個……(答)
の4個……(答) であるものは,
であるものは, と
と と
と と
と と
と と
と の6個……(答)
の6個……(答)


 ……(答)
……(答)





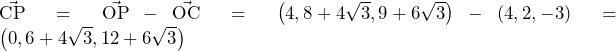
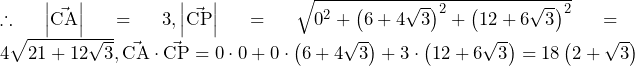
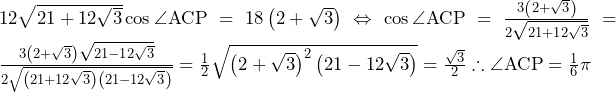 ……(答)
……(答)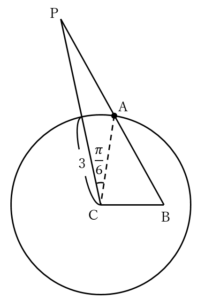

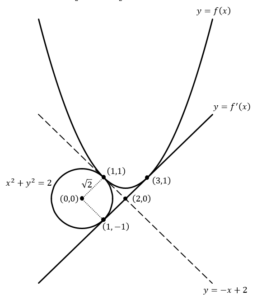
![Rendered by QuickLaTeX.com \left(\sqrt2\right)^2-\frac{1}{4}\cdot\pi\left(\sqrt2\right)^2+\int_{1}^{2}\left\{\frac{1}{2}x^2-2x+\frac{5}{2}-\left(-x+2\right)\right\}dx+\int_{2}^{3}\left\{\frac{1}{2}x^2-2x+\frac{5}{2}-\left(x-2\right)\right\}dx=2-\frac{1}{2}\pi+\left[\frac{1}{6}x^3-\frac{1}{2}x^2+\frac{1}{2}x\right]_1^2+\left[\frac{1}{6}x^3-\frac{3}{2}x^2+\frac{9}{2}x\right]_2^3=\frac{7}{3}-\frac{1}{2}\pi](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-44afce5ecd37028422cb4028e4e5fbca_l3.png) ……(答)
……(答)
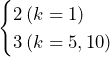
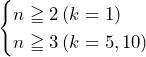 のとき……(答)
のとき……(答)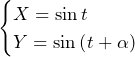
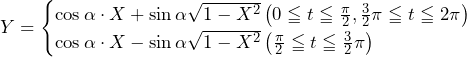
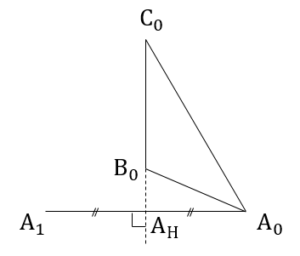
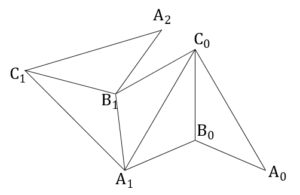
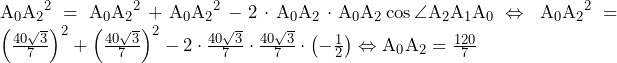 ……(答)
……(答)
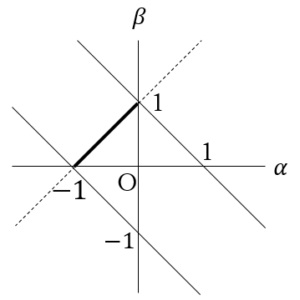
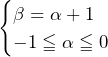
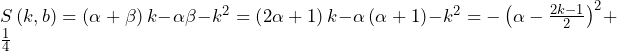
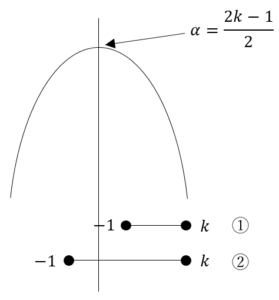
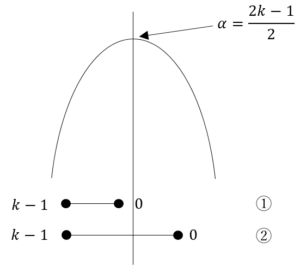
![Rendered by QuickLaTeX.com \int_{-1}^{-\frac{1}{2}}\left(-k^2-k\right)dk+\int_{-\frac{1}{2}}^{0}\frac{1}{4}dk+\int_{0}^{\frac{1}{2}}\frac{1}{4}dk+\int_{\frac{1}{2}}^{1}\left(-k^2+k\right)dk=\left[-\frac{1}{3}k^3-\frac{1}{2}k^2\right]_{-1}^{-\frac{1}{2}}+\left[\frac{1}{4}k\right]_{-\frac{1}{2}}^0+\left[\frac{1}{4}k\right]_0^{\frac{1}{2}}+\left[-\frac{1}{3}k^3+\frac{1}{2}k^2\right]_{\frac{1}{2}}^1=\frac{5}{12}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-e0c8bfe825912f02cafeb7f3d4b9999f_l3.png) ……(答)
……(答)