方針の立て方
殆ど全てが基本問題であり特筆事項なし.
最後の面積は,円形の部分の面積を求めるのに工夫が必要である.円の積分は(文系数学の範囲では)出来ないため,解析的にではなく幾何学的に求めることになると判断しよう.
解答例
(ⅰ)
(ウ)![]()
(ⅱ)
(4)![]()
(5)![]()
(6)![]()
(7)(8)![]()
(9)![]()
(10)(11)![]()
(ⅲ)
(エ)![]()
(ⅳ)
(12)(13)![]()
(14)(15)![]()
(16)(17)![]()
(18)![]()
(19)![]()
(20)(21)![]()
(22)(23)![]()
解説
(ⅰ)(ⅱ)
![]()
放物線![]() と直線
と直線![]() の接点を
の接点を![]() とすると,接線は
とすると,接線は![]() と表せる.これが
と表せる.これが![]() と一致するので,係数比較すると,
と一致するので,係数比較すると,

よって,![]() ……(答)
……(答)
また,![]() より接点の座標は,
より接点の座標は,
![]() ……(答)
……(答)
放物線![]() と直線
と直線![]() の接点についても,同様に考える.接点を
の接点についても,同様に考える.接点を![]() とおくと,
とおくと,![]() より,接線は
より,接線は![]() と表せる.これが
と表せる.これが![]() と一致するので,係数比較すると,
と一致するので,係数比較すると,
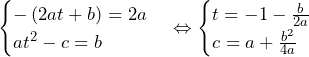
よって,接点![]() の座標は,
の座標は,
![]() ……(答)
……(答)
(ⅲ)
原点と直線![]() の距離は,点と直線の距離の公式より
の距離は,点と直線の距離の公式より![]() .よって,直線
.よって,直線![]() が原点を中心とする半径
が原点を中心とする半径![]() の円
の円![]() と接するための必要十分条件は,
と接するための必要十分条件は,
![]() ……(答)
……(答)
(ⅳ)
接点![]() の座標は,円
の座標は,円![]() の式が
の式が![]() であることより,
であることより,
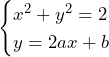
![]() を用いてこれを解くと,
を用いてこれを解くと,
![]() (重解)
(重解)
となる.よって,接点![]() の座標は
の座標は![]() .
.
これが点![]() と一致するのは,
と一致するのは,
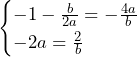
![]()
![]() は正の実数のため,
は正の実数のため,![]() が適当.これを条件(A)の式:
が適当.これを条件(A)の式:![]() に代入すると,
に代入すると,![]() .
.
![]() ……(答)
……(答)
このとき,円![]() と放物線
と放物線![]() の共有点は,
の共有点は,
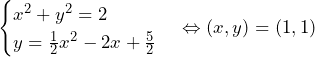
より,![]() ……(答)
……(答)
放物線![]() ,直線
,直線![]() ,円
,円![]() :
:![]() を図示すると,
を図示すると,
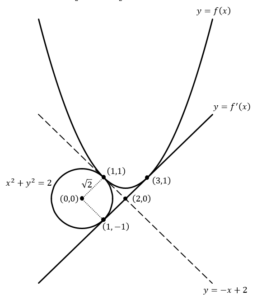
上図.点![]() の4点を頂点とする正方形内について考えると,題意を満たす領域の面積は,正方形から四分円を引いた面積と等しくなるため,
の4点を頂点とする正方形内について考えると,題意を満たす領域の面積は,正方形から四分円を引いた面積と等しくなるため,
![]()
と書ける.
よって,求める面積は,
![Rendered by QuickLaTeX.com \left(\sqrt2\right)^2-\frac{1}{4}\cdot\pi\left(\sqrt2\right)^2+\int_{1}^{2}\left\{\frac{1}{2}x^2-2x+\frac{5}{2}-\left(-x+2\right)\right\}dx+\int_{2}^{3}\left\{\frac{1}{2}x^2-2x+\frac{5}{2}-\left(x-2\right)\right\}dx=2-\frac{1}{2}\pi+\left[\frac{1}{6}x^3-\frac{1}{2}x^2+\frac{1}{2}x\right]_1^2+\left[\frac{1}{6}x^3-\frac{3}{2}x^2+\frac{9}{2}x\right]_2^3=\frac{7}{3}-\frac{1}{2}\pi](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-44afce5ecd37028422cb4028e4e5fbca_l3.png) ……(答)
……(答)









Published by