方針の立て方
(ⅰ)(ⅱ)ともに典型問題であるため,特筆事項なし.
解答例
(ⅰ)
(1)![]()
(2)![]()
(3)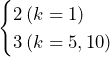
(ⅱ)
(ア)![]()
(イ)![]()
解説
(ⅰ)
![]() は初項
は初項![]() ,公比
,公比![]() の等比数列であるから,
の等比数列であるから,
![]()
である.
![]()
〇![]() を満たす
を満たす![]() ((1)について)
((1)について)
![]() の場合,
の場合,![]() であるから,
であるから,![]() を満たすには,
を満たすには,
![]()
であれば必要十分.![]() のとき,この不等式は満たされる.
のとき,この不等式は満たされる.
![]() ……(答)
……(答)
〇![]() が100の倍数となる
が100の倍数となる![]() が存在する場合((2)と(3)について)
が存在する場合((2)と(3)について)
10以下の自然数![]() で
で![]() が100の倍数となることはない.
が100の倍数となることはない.
10以下の自然数![]() の内,
の内,![]() が
が![]() の倍数となる
の倍数となる![]() が存在するものを考える.
が存在するものを考える.
![]() のとき,
のとき,![]() であり,これは任意の
であり,これは任意の![]() で100の倍数となる.
で100の倍数となる.
![]() のとき,
のとき,![]() であり,素因数5を含まないため全ての
であり,素因数5を含まないため全ての![]() で100の倍数とはならない.
で100の倍数とはならない.
![]() のとき,
のとき,![]() であり,素因数5を含まないため全ての
であり,素因数5を含まないため全ての![]() で100の倍数とはならない.
で100の倍数とはならない.
![]() のとき,
のとき,![]() であり,素因数5を含まないため全ての
であり,素因数5を含まないため全ての![]() で100の倍数とはならない.
で100の倍数とはならない.
![]() のとき,
のとき,![]() であり,これは
であり,これは![]() のとき100の倍数となる.
のとき100の倍数となる.
![]() のとき,
のとき,![]() であり,素因数5を1つしか含まないため全ての
であり,素因数5を1つしか含まないため全ての![]() で100の倍数とはならない.
で100の倍数とはならない.
![]() のとき,
のとき,![]() であり,素因数5を含まないため全ての
であり,素因数5を含まないため全ての![]() で100の倍数とはならない.
で100の倍数とはならない.
![]() のとき,
のとき,![]() であり,素因数5を含まないため全ての
であり,素因数5を含まないため全ての![]() で100の倍数とはならない.
で100の倍数とはならない.
![]() のとき,
のとき,![]() であり,素因数5を含まないため全ての
であり,素因数5を含まないため全ての![]() で100の倍数とはならない.
で100の倍数とはならない.
![]() のとき,
のとき,![]() であり,これは
であり,これは![]() のとき100の倍数となる.
のとき100の倍数となる.
以上より,![]() が100の倍数となる
が100の倍数となる![]() が存在するような10以下の自然数
が存在するような10以下の自然数![]() は
は![]() の3つ……(答)
の3つ……(答)
また,このとき,![]() が100の倍数となるのは,
が100の倍数となるのは,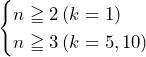 のとき……(答)
のとき……(答)
(ⅱ)
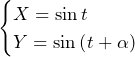
とおくと,加法定理より,
![]()
であるから,
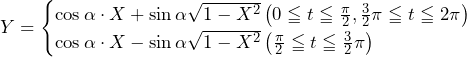
となる.
〇![]() が線分となるような
が線分となるような![]() の値((ア)について)
の値((ア)について)
![]() が線分となるのは
が線分となるのは![]() の係数
の係数![]() が0となるとき.
が0となるとき.
![]() ……(答)
……(答)
〇![]() が原点を中心とする円となるような
が原点を中心とする円となるような![]() の値((イ)について)
の値((イ)について)
![]() が原点を中心とする円となるのは
が原点を中心とする円となるのは![]() の係数
の係数![]() が0となるとき(そのとき
が0となるとき(そのとき![]() となり
となり![]() の式は
の式は![]() となる).
となる).
![]() ……(答)
……(答)









Published by