慶應義塾大学文学部の英語は、他大学に比べても非常に難関 です。
しかし、
合格点を取れないからといってあきらめる必要はありません。
本ブログでは、慶應文学部の英語試験の特徴と対策を解説しています。
慶應文学部の英語では、和訳問題と要約問題で半分程度の点数 があります。合否の鍵 を握ります。
[toc]
慶應文学部の英語の全体像/問題傾向
大問
種類
語数
Ⅰ
長文問題(記述形式)
約2000words
特殊な問題の多い慶應義塾大学の中でもかなり特殊な問題の出題になります。
なんと、
英語長文大問1題
問題数は10問程度であることが多く、※ 稀に長文が2問出る年もありますので、覚悟はしておく必要があるでしょう。
英文の抽象度高い 文章の抽象度が私大では最難関レベル となっています。常に筆者の主張を確認すという読み方
難しい慶應文学部の英語長文をどのように読んだら良いのか?をこちらの記事で伝えているので、過去問をやってみたけど難しすぎて読めない・・・という人 は、確認してみましょう。
慶應文学部の英語は何点取れば良いのか?
英語は数ある大学の中でもトップレベルで難しい大学学部です。
150点中90~110点(60~70%)は取れるようにしておきましょう
*難しい時と簡単な時の差がすごいので、100点越えを安定して取れるようにしたいです。
なぜそれだけの点数を取らなくてはいけないのかを、
慶應文学部の合格最低点
外国語:150/350点 時間120分
年度
配点
合格最低点
得点率
2023
350
205
58.6%
2022
350
218
62.3%
2021
350
232
66.3%
2020
350
250
71.4%
[word_balloon id="1" balloon="line" name_position="under_avatar" name="ブタトン" radius="true" avatar_border="false" avatar_shadow="false" balloon_shadow="false" avatar_hide="false" box_center="false" font_size="17" name_color="#10193a" position="R" bg_color="#8de055" font_color="#fff"]国公立と同じで記述が全体的に多いので要注意。他の学部よりも大きく合否に影響 してくるので要注意です。[/word_balloon]
慶應文学部の小論文の対策記事はこちらからどうぞ。
慶應文学部の問題の読解、問題の対策
ここからは、長文問題の読解、それぞれの問題に対しての対策をお伝えいたします。 [word_balloon id="1" position="L" size="M" balloon="line" name_position="under_avatar" radius="radius_12" avatar_border="false" avatar_shadow="false" balloon_shadow="true" font_color="#ffffff" bg_color="#70a6ff" font_size="22" balloon_full_width="true"]どのような形で慶應文学部の長文の対策をしたら良いのかをお伝えしていきますね![/word_balloon]
慶應文学部の英語の平均点
年度
英語
得点率
2024
62.73
41.8%
2023
66.61
44.4%
2022
73.95
49.3%
2021
77.32
51.5%
2020
99.38
66.3%
2019
88.46
59.0%
2018
80.11
53.4%
2017
85.68
57.1%
2016
92.69
61.8%
2015
75.86
50.6%
2014
70.86
47.2%
2013
67.99
45.3%
2012
73.65
49.1%
2011
79.18
52.8%
2010
74.43
49.6%
慶應文学部は問題形式が基本的に同じなので、少し多めに平均点を見ておきましょう。
英語の平均点が低いと
過去問をやってちゃんとできたのに・・
過去問で満点近くの点数が取れていても、本番で急にできなくなる・・というのは、「文学部あるある」です。本番「難しい!」と感じてもできる部分を確実に取れるようにしていくのが重要 です。
慶應文学部の設問ごとの配点予想
大問
種類
難易度
配点
I
和訳問題
★★
45点(1問15点)
II
空所補充
★★
20点
III
説明問題
★★★
35点(2問)
IV
要約問題
★★★★
30点
V
英訳問題
★★★
20点
空欄補充は毎年出るか不明ですが、それ以外は同じ形式の問題です。
1問の点数が非常に大きい!
上述していたように1問の点数が10点は少なくともあると考えられるため、1問間違えてしまうとそれだけで非常に大きいです。
慶應文学部に合格するには和訳と説明問題が合否の鍵
慶應文学部に合格したいのであれば、
和訳(45点相当)と説明問題(35点相当) は落とすことができません。
2つの設問で、英語の点数の半分以上を占めています。
この設問を落とす→残念ながら、不合格となってしまいます。
短期間で対策をしたいのであれば・・
一見難しい慶應文学部ですが、和訳と説明問題の対策をするだけで合格に近づくことは可能 です。
例年、自己推薦で落ちた生徒をそこから(高3/11,12月頃〜)対策することがあるのですが、英語、社会を短期間でクリアして合格水準まで仕上げています。
【慶應文】英語の時間配分はどうするのか?
慶應文学部は,
しかし、過去問を解いてみるとわかると思いますが、時間はギリギリになると思います。
下記目安の時間配分を掲載しておきますのでご覧ください。
問題形式
所要時間
和訳問題
10分×3
空所補充
5分×2
説明問題
15分×2
要約問題
30分
英訳問題
10分
注意!
【慶應文】長文問題をまずはちゃんと読めるように!
長文問題ができるようになるためには、
もちろん、たくさん解くというのは結果的には重要なのですが、、
慶應文学部に合格したいのであれば・・・
闇雲に過去問をたくさん解くのではなく、まずは文章の意味(筆者の主張)、文章の構成を理解しながら読み込んでいくのが重要です。
文章の構成、繋がりとはどういうことか?
文章のつながり、構成というのがわからないと思いますので、
まずは下記の文章を読んでみましょう。
Western civilization’s foray into Asia brought about intricate changes in the tapestry of the continent. The 19th-century colonial pursuits introduced a spectrum of Western thought, technological advances, and cultural nuances. These colonial footprints led to the inception of European linguistic capacities and the adoption of governance structures reminiscent of Western paradigms. The debate surrounding these influences oscillates between the spectrum of modernization and the erosion of indigenous values. The confluence of Eastern and Western dynamics has fashioned a unique cultural mosaic, with the reverberations of this historical interaction continuing to influence the contemporary Asian landscape.
単語が難しいのもそうですが、
続いて、下記文章を読んでみましょう。
Firstly , it’s important to understand that when Western civilization ventured into Asia, it caused significant and complex changes across the entire continent. For instance , in the 19th century, as European countries pursued colonial ambitions, they brought with them a range of Western ideas, cutting-edge technologies, and distinct cultural practices. As a result of this colonization, many Asian regions began to learn European languages and even adopted governance systems that were similar to those in the West. Moreover , there has been an ongoing debate about these changes: on one hand, some believe they brought about modernization; on the other hand , there’s a perspective that it led to the fading of local traditions and values. Interestingly , as the East met the West, a special blend of cultures emerged. In fact , this blending of traditions and influences still plays a role in shaping modern-day Asia.
ほとんど同じ内容なのですが、
使われている単語のレベル
ディスコースマーカーの増加
節が増加
【慶應文】英語を読めるためには?
単語については、辞書が使えるので良いとして、
*もちろん、それ以外に難しい理由としては、普段読み慣れてない随筆のような文体もでたりして読みづらい場合があります。
【慶應文】よくある間違った読み方とは?
ここまで述べてきている通り慶應文学部の英語は非常に難しいです。
ご自身が読んでいる際に、下記の点を注意して読めているのかを確認 してください。
確認1:適切な語義が選択できていますか?
文章を読んでいてよくわからないときは、
単語の意味は、文章内で他の単語との関係性で意味が決まってきます。
文章を読んでいて、どうしても意味がよくわからないという場合は、単語の意味を取り違えている意味があります。
品詞が違うと違う意味になったり、
確認2:文章をつなげて読めていますか?
先ほどから伝えている部分ではありますが、、
注意!
ということです。
文章がどのようにつながっているのか?理解していない人が多いです。
下記ブログ記事にて、どのようにつながっているのかお伝えしています。
【慶應文学部】長文の設問ごとの対策
ここからは、大問ごとの問題傾向について、お伝えしていきます。
まずはほとんど確実に出題が予想される問題形式での問題の対策を見ていきましょう。
和訳問題
説明問題
和文英訳問題
要約問題
1,和訳問題の対策とは?
これは慶應大学文学を合格したいのであれば、落とすことはできません。
和訳問題なのに構文すらも見抜けないのでは、
和訳問題ですが、まず確認すべきことは文法的に文章を読めているかどうかという点です。
もちろん、過去問をおこなっていてまだまだ不十分と感じるようであれば、
対策の仕方としては、ポレポレ英文読解プロセス50 といった基本的な構文問題集をSVOCがわかるように何度も何度も繰り返しおこなってください。
また、こちらのページに 具体的にどのような形で慶應文学部の和訳問題の対策をしたら良いのかを記載しましたのでご覧ください。
[nlink url="https://hiroacademia.jpn.com/blog/taisaku/keio/bungaku/keiobun-wayaku/"]
2,説明問題の対策とは?
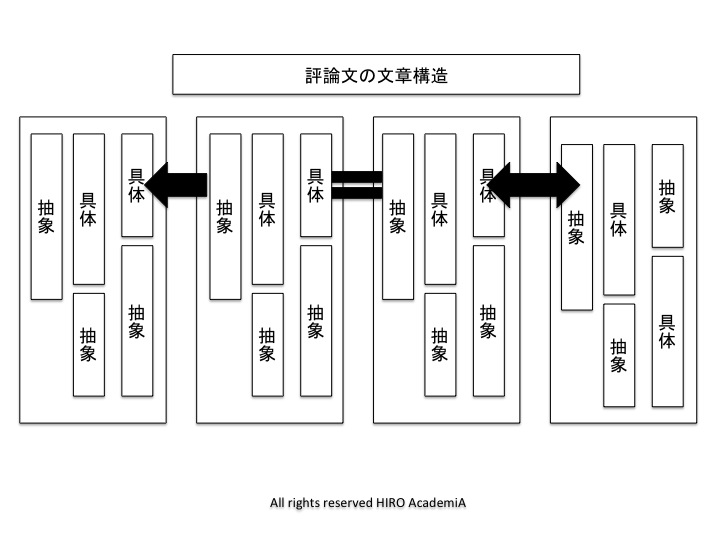
具体的にはどういうことか?ということが問われる問題です。まず1つのパラグラフが以下のように具体と抽象部分で構成されているということを理解しなくてはいけません。
その場合は、抽象部分の言いたいことを図式化して主張の構造を掴んで、
設問文からどのようなことを聞かれているのかを理解していくことも
本説明問題を解く上ではかなり重要です。
下記ブログ記事よりご確認下さい。
[nlink url="https://hiroacademia.jpn.com/blog/taisaku/keio/bungaku/keio-bun-cheat/"]
3,和文英訳問題の対策とは?
まずは基本的な英作文パターンを覚えていきましょう。
基本的な英文法を自由自在に使いこなせるのはもちろんのこと、 特に、主語、時制、論旨の接続の仕方には十分に注意してください。
難易度は、英作文問題としては標準レベルで難しくはありません。当塾では「ドラゴンイングリッシュ 」を行うことをオススメ しています。
また、本問題は文章内の表現を使ってということは明示されてはいないですが、
文章内の表現を使うことで簡単に解けることもあります。
表現がすぐに見つかるようでしたら、長文内の文章を利用して解いてみてください。
4,要約問題の対策とは?
慶應義塾大学の合格をめざすのであれば、落とすことのできない問題です。 英語の読解力はもちろんですが、現代文の要約能力も問われています。
問われている字数が100-120字なので、
ですが、不要な要素を含めたり、同じことを長く書いても点数をあげることはできません。
対策としては、過去問を実施するのが一番良いですが、
過去問以外でも自身で普段から長文の要点をまとめる練習をすると良い
要約というのは、筆者の意見をまとめるのが基本となります。
筆者の意見を補強するために使われている具体例を含めないように注意してください。
要点を書き出して、どの要素が必要かをわかってから記載するようにしてください。
具体的な対策はこちらの記事でどうぞ。
[nlink url="https://hiroacademia.jpn.com/blog/taisaku/keio/bungaku/keio-bun-en-summary/"]
【頻度|低】出題される問題
ここからは、毎年出題されるわけではないけれど、
空欄補充問題の対策とは?
空欄補充問題を慶應の文学部では出題されます。 この問題は和訳問題の範囲が小さい問題だと思ってもらって構わないです。
同タイプの問題なので、1つのパラグラフから全体の意味をつかむことが肝心です。
パラグラフ並び替え問題の対策とは?
解き方として、代名詞や時制をチェック
慶應文学部の出典とは?
慶應文学部の問題は基本的に最初にタイトルが記載されています。Who Ate the First Oyster? Philosophical baby The Animals Among Us The coming-of-age con 出典:aeonAttached to Technology and Paying a Price 出典:New York timesDoes spelling matter? 出典:同名の文庫本
慶應文学部での辞書の持ち込みについて
慶應文学部で必要な語彙力は早慶では高くありません。使用されている語彙のほとんどが見たことのあるレベルのものになるでしょう
辞書2冊は何が良いですか?
慶應文学部は辞書2冊を許可しています。英和と和英辞書
どの辞書を持って行ったら良いのか?について具体的にはこちらに記載しています。
[nlink url="https://hiroacademia.jpn.com/blog/taisaku/keio/bungaku/keio-bun-dictionary/"]
慶應大学に合格する英語力を鍛える勉強法とは?
WP Fastest Cache
慶應大学に合格するためには、
こちらのページにて慶應大学に合格するために、どのような力が必要で、どのようなことを勉強したら良いのかを説明しています。
[nlink url="https://hiroacademia.jpn.com/blog/taisaku/keio/keio-eigo-benkyoho/"]
慶應文学部に絶対合格したいならヒロアカへ!
慶應専門塾のヒロアカは、「慶應義塾大学文学部合格」 に圧倒的な自信を持っています。少数精鋭 だからこそ、開塾以来、毎年必ず慶應文学部の合格者を輩出 してきました。
慶應文学部に合格するには過去問だけでは不十分!
慶應義塾大学文学部の入試は記述問題が多数 出題され、的確な和訳・英作・要約指導 が合格のカギを握るのです。
ヒロアカでは、一人ひとりの弱点を見極めたカリキュラム を組み、
基礎からの読解力向上
答案の論理構成
記述答案の個別添削
など、合格のための最短ルートを一人ひとりに合わせて指導しています。
まずはお気軽にお問い合わせを!
無料カウンセリングや体験授業もご用意しております。実際の指導内容や記述添削のクオリティを、ぜひ直接ご確認ください。

















![Rendered by QuickLaTeX.com \int_{0}^{2}\left(-6x+15\right)dx=\left[-3x^2+15x\right]_0^2=18,\int_{0}^{2}\left(-3x^2+12\right)dx=\left[-x^3+12x\right]_0^2=16](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-c3bfa33edb30774157f6fafbfffed269_l3.png)
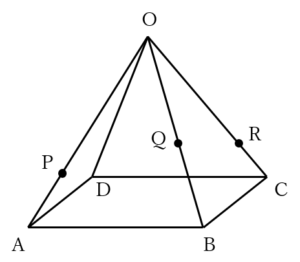
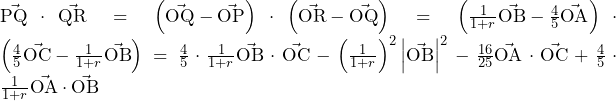
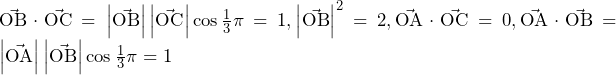 であるから,
であるから,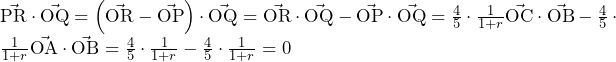 ……(答)
……(答)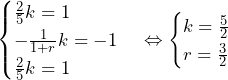
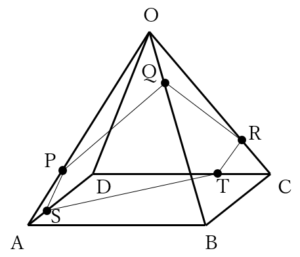
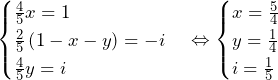
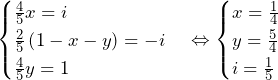
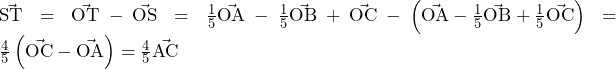
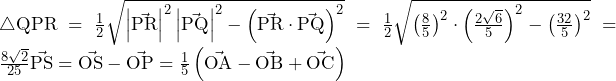 より,
より,