早稲田文・文化構想に合格したいのであれば、要約は重要 早稲田大学文学部・文化構想学部の英語は全体で75点満点。 そのうち、大問Ⅴの英文要約はわずか5点(公表されてませんがヒロアカでの採点)と一見すると配点は小さく見えます。 しかし、合格最低点が3科目合計200点中の130〜135点程度であることを考
- …続きを読む
-
早稲田文・文化構想に合格したいのであれば、要約は重要
早稲田大学文学部・文化構想学部の英語は全体で75点満点。
そのうち、大問Ⅴの英文要約はわずか5点(公表されてませんがヒロアカでの採点)と一見すると配点は小さく見えます。しかし、合格最低点が3科目合計200点中の130〜135点程度であることを考えると、
この5点をしっかり取り切れるかどうかで合否に大きな差がつきます。実際、多くの受験生は“大問Ⅴは割と勘で解いてしまう”ことが多く、
その結果、ほかの大問である程度点を取っていても要約問題で落としきれない失点が重なり、合格ラインに届かないというケースが珍しくありません。だからこそ、意外と侮れないこの5点を確実に手中に収めることが、早稲田文・文化構想合格への鍵になるのです。
合格するためには確実に取りたいのがこの問題です!

感覚で答えを出している人がほとんど
要約問題を苦手とする受験生の多くは、文章全体の流れやロジックを追わずに“なんとなく”の感覚で答えを埋めてしまいがちです。
筆者の主張や論拠、対比などの論理構造を理解せず、“単に英文を短くしたつもり”になってしまうのです。しかし、実際には、論理構造を把握して正確に理解をする必要があります。今回のブログ記事では、文・文化構想の問題を解く上で超重要な基本論理構造の9パターンをお伝えします。

感覚に任せるだけでは、的外れな内容になってしまい、5点中2〜3点を落とす結果に直結します。
早稲田レベルで英語を攻略するには、“要約=文章構造の再構築”という視点が欠かせません。ヒロアカでは他塾ではできない論理構造の指導を細かく実施
ヒロアカでは、英文要約を単に内容を書き抜くだけのトレーニングではなく、
論理構造をきちんと理解したうえでまとめるスキルとして指導しています。多くの塾では時間の都合上、ここまで踏み込んだ指導は難しいのが現状ですが、
ヒロアカなら英語全体の点数アップのみならず、合格をさらに引き上げられるサポートを提供しています。早稲田文・文化構想の要約はまずは読解が重要
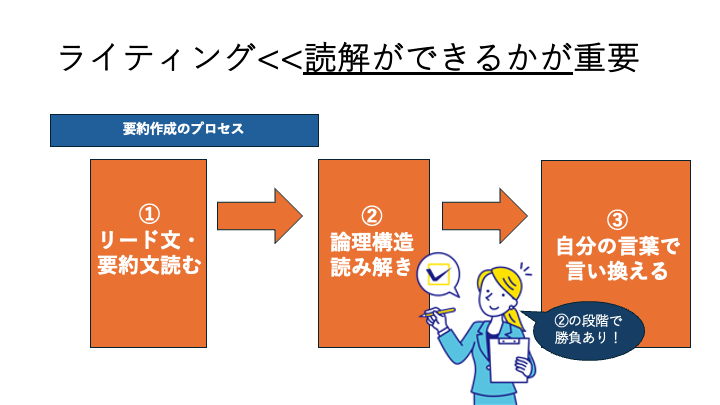
早稲田文学部・文化構想学部の要約は、
“自分の言葉で書くこと”が想像されがちですが、
実際はまずは文章を読み解くところからが重要になっています。ほとんどの人が論理の構造を理解できてないです。

英検準1級の要約対策でもこの辺りの話はふれているので興味のある人はどうぞ。
[nlink url="https://hiroacademia.jpn.com/blog/kentei/eigokentei/grade-pre1/eiken-pre1-yoyaku/"]要約には論理構造の理解が必要不可欠
要約とは、文章を短くするだけではなく、
「筆者が本当に言いたい要点」を読み手自身が組み立て直す作業です。もし文章中に「AとBを対比し、最後にCという結論に至る」ような論理の流れがあるのに、
単に「AとBが出てきました」だけを述べても、筆者の言いたい結論(C)は分かりません。文章全体を貫く主張の道筋(論理構造)を追わないと、肝心な結論や主張を的確に把握できないのです。
英語長文ができない子は、文章を1文1文で繋がりを考えずにバラバラに捉えがちです。
でも論理構造がわからないと、文章を理解するのは不可能です。
論理構造とは?
簡単にいうと、文や文章のなかで「どうしてそうなるの?」とか「これとこれを比べてどう違うの?」という
考え方の道すじ(話の“すじ道”や“つながり方”を表すルール)のことです。たとえば、算数で「1 + 1 = 2」は、“1たす1”が“2になる”理由がはっきりしていますよね。
これと同じように、文章でも「どうしてAになるのか?」や「なぜBという結論が出てくるのか?」というつながりを
示している部分が、論理構造です。
早稲田文学部、文化構想学部の要約で合格点を取るためには、
論理構造を理解することが必要不可欠。論理構造が分かると「どこが重要か」が明確になる

文章にはしばしば例え話や細かい補足、背景情報などの「枝葉的情報」が混在しています。
しかし、論理構造を理解できれば、
「ここは結論に直結する重要な根拠だから押さえる」
「ここは具体例を示すための挿話だから概略だけ拾えばいい」と、
情報の取捨選択が容易になります。筆者の「意図」と「立場」が見える
論理構造には、
たとえば「相手の反論を紹介したあと、自分の見解を示す」や「Aという前提からBが導かれる」など、
筆者が意図的に組んだ展開の順序が表れます。この展開の順序を追うと、
筆者が「読者をどの方向へ導きたいか」「どの部分を強調したいか」がわかります。したがって要約のときも、どの見解が筆者自身の意見で、どれが引用・批判・反駁などの“借りてきた意見”なのかを区別しながらまとめられます。
論理構造にはパターンがある

文章を読んでいると、「筆者は何を言いたいんだろう?」とか「どうしてこの結論になるんだろう?」と感じることはありませんか?
実は、文章はただ思いついたことを順番に並べているわけではなく、
“結論までの道すじ”をあるパターンに沿って組み立てている ことが多いのです。
たとえば、友達同士の会話でも、無意識に「こうだからこうなるよね」という 因果関係 を使ったり、「AよりBのほうがいいんじゃない?」という 対比 で話したり、「○○するためには××が必要だよね」という 目的と手段 の流れを使ったりしているはずです。
文章を読むときに、この “結論までの道すじ” がどんなパターンに当てはまるのかを見極められると、
内容をすばやく整理して「要点はここだ!」と見つけやすくなります。パターンを理解することができれば、早稲田文学部、文化構想学部での未知の問題に瞬時に対応することができます。
絶対に理解をしたい!基本論理構造9パターン
下記は、早稲田大学の問題を理解する上で超重要な基本論理構造の9パターンになります。
パターン 特徴 理解するために必要な視点 パターン1: 対比 (Comparison/Contrast) AとBを並べて差異や矛盾を強調する。「しかし」「一方で」などの対立表現が目印。 対立するキーワードを確認し、両者の立場・評価を整理する。 パターン2: 因果 (Cause & Effect) 原因A → 結果Bという流れ。「〜のために」「〜の結果として」などが目印。 原因と結果を取り違えないよう整理する。 パターン3: 目的 (Goal) と手段 (Means) 目的を達成するために具体的な手段がとられる。「〜するために」などが目印。 目的と手段を明確に区別して読む。 パターン4: 逆説 (Paradox) 一見矛盾する事象や、解決策が逆に問題を起こす構造。「しかし実は」「一方で」などで強調される。 見かけと実際の食い違いに着目する。 パターン6: 問題-解決 (Problem-Solution) 問題を提示→解決策→その影響・限界を示す流れ。 問題と提案策の関係、および成否を押さえる。 パターン7:定義 → 例示 (Definition → Example) まず概念を定義し、次に例を挙げて理解を深める構成。 定義を表す語句を見つけ、例示と照らし合わせる。 パターン8: 帰納 (Inductive Structure) 複数の具体データを積み重ね、最後に一般的な結論を導く。 複数事例の共通点からどんな結論を導いているか見る。 パターン8: 漸次展開 (段階的な拡大・累積) 個人・局所の話から徐々に社会・世界へ話を広げ、最終的に大きな結論を示す。 どの段階でスケールが拡大しているかを追う。 パターン9: 反論と再反論 (Counterargument → Rebuttal) 相手の主張を先に示し、データや理論で切り返して自説を補強する構造。 相手の立場と、それに対する反証・根拠を関連づけて整理する。 ここからはそれぞれのパターンをひとつずつ解説していきます。
パターン1:対比
特徴
AとBを並べ、差異・矛盾点を指摘することで主張を際立たせる
「しかし」「一方で」「逆に」「vs.」などの対立を示す接続詞・語句が目印出題年度
2024年: “多様性は分断を生む”という否定的見解 vs. “実際は全体の定員拡大で既得権も守られた”という反証
2021年: “速読”vs.“遅読”
2017年: “毒殺説・激しい対立”vs.“実は協力関係だった”
2014年: “電子書籍のメリット”vs.“紙の本の読書体験”理解するためには何が必要か?
対立を示すキーワード(but, however, on the other hand など)を見逃さない。
対比する要素が文中でどのように評価(正・負)されているか把握し、それぞれの立場や結果を整理する。パターン2:因果
特徴
原因(原因A)→結果(結果B)という流れ
「なぜなら」「〜のために」「〜の結果として」などが目印出題年度
2022年: 気候変動(原因)→ 極端気象の頻発・巨大化(結果)
2019年: 社会的ステレオタイプや他者の言説(原因)→ アイデンティティ形成のあり方へ影響(結果)
2013年: 都市の魅力(原因)→ 若者の流出→ 農村部の過疎化・衰退(結果)
(部分的に)2021年: 読むスピード上昇(原因)→ 理解度低下(結果)
(部分的に)2020年: 大量の忘却が起こる(前提)→ それでも自己は維持される(結論的メッセージ)理解するためには何が必要か?
因果を示す接続詞(because, since, as a result, therefore など)に注目。
「どの要素が原因で、何が結果なのか」を混同せず明確にする。パターン3:目的と手段
特徴
ある意図・目的があり、それを達成するために何らかの手段や施策がとられる
「〜するために」「〜を狙って」「目的は〜だ」などが目印出題年度
2018年: 「植民地支配を円滑にする」= 目的 → 「英文学教育を導入」= 手段
キリスト教布教の代替策として英文学を使い、イギリス的価値観を浸透させる理解するためには何が必要か?
筆者が何を最終的に成し遂げたいのか(目的)をまず読み取り、その手段としてどんな具体的行動や政策が提示されているかを区別する。
パターン4:逆説
特徴
一見すると矛盾しているような事象や、解決策が却って問題を引き起こす構造
「しかし実は」「一方ではこうなる」など、論理的ギャップを強調する記述が多い出題年度
2020年: 大量の記憶を失っているのに、自己同一性が保たれる=「一見矛盾だが実は成立する」
2015年: 図書館の書架・紙の劣化問題を解決するためのマイクロフィルムが、逆に劣化してしまう理解するためには何が必要か?
表面上の常識と、実際の結末が食い違う部分を捉える。
「本来はこうあるべきだが、実は反対になっている」という流れを明確に区別して理解する。パターン5:問題-解決
特徴
序盤で「このままでは○○という問題がある」と問題点を明確化し、途中または終盤
で「そこで××という手段が考えられる」と解決策を示す。さらに、その結果どうなるか(メリット・デメリット)に言及することが多い。
例:ある問題を提示 → 解決策を提示 → その解決策の影響や限界を述べる出題年度
図書館の「書架不足」や「酸性紙の劣化」という問題(2015年の例)に対して、マイクロフィルム化という解決策を実施 → 逆説的に失敗する、という流れが典型。
理解するためには何が必要か?
「どんな問題点があり、提案された方策が何か」を簡潔に押さえ、その方策が成功したのか失敗したのか、あるいは部分的だったのかを確認する。
パターン6:定義 → 例示
特徴
見慣れない概念(専門用語)をわかりやすく説明し、その後に具体例をいくつか挙げて実感を伴った理解を促す。結論(主張)が最後にまとめられる。
例:ある概念をまず定義 → 具体的な事例・数字・逸話などを提示 → 結論を導く出題年度
2020年の記憶・忘却の箇所などで、「記憶」「忘却」「失われたニューロン」といった概念の簡単な定義や解説 → 個人の体験例や一般的事例 → 「それでもアイデンティティは保たれる」という結論につながる。
理解するためには何が必要か?
定義の文(is defined as, refers to, meansなど)を見つけ、そこに続く具体例を探して照らし合わせる。
用語の使い方や筆者がそこに付与しているニュアンスを理解する。パターン7:帰納
特徴
冒頭から事例A・B・Cと次々に挙げ、「以上のことから○○が言える」という形で結論に至る。問題解決策や大きな主張よりも「傾向」「特徴づけ」「法則」などを導き出すために使われる。
例:小さな具体例・データ・事象の積み重ね → 一般的な結論を提示出題年度
2013年の都市化の話は、世界人口の統計・農村と都市の対比的な事実を順に並べる → 「これらの事例(人口移動・農村インフラ縮小)から、今や世界は都市中心になりつつある」と導くなど。
理解するためには何が必要か?
複数の具体例をまとめ、そこから導かれる共通点・法則を見出す意識を持つ。
事例A・B・Cをどう総合し、最終的に何を結論づけているかを確認。パターン8:漸次展開
特徴
序盤は個人の事例や単発の調査結果などを提示し、「このような個別の問題は実は社会全体にも当てはまる」と範囲を広げていく。段階的に視点を移しながら、最終的に普遍的な主張へ結びつける。
例:はじめに小さな視点(個人・局所) → 徐々に範囲を広げて社会全体・世界的視点へ → 大きな結論出題年度
2019年のアイデンティティの例は、まず個人の日常行動と「他者からの見られ方」を論じる → 次第に「社会的ステレオタイプ」「大衆メディアの影響」→ 結局、個人のアイデンティティは社会全体の言説と連動している、という大きな帰結を提示。
理解するためには何が必要か?
「筆者が話のスケールをどのように広げているか」をパラグラフの流れで見る。
「個人→社会」または「ミクロ→マクロ」のステップに注目し、どこで視点が拡大されているかをチェック。パターン9:反論と再反論
特徴
まず相手方の立場(通説・一般的イメージ・批判)を紹介し、それに対して筆者独自の根拠(データ、理論)を提示して切り返し、最終的に自説を補強する。説得力を高めるために使われる。
例:「Aという主張があるが、実際にはBというデータや事例がある。よってAは正しくないか、あるいは限定的である」出題年度
2024年の多様性議論は、「多様性は既存の特権層を脅かす」「差異を強調し過ぎる」という批判 → 実際の数字(既存層の減少はなかった) → 結論(むしろ多様性はコミュニティを強化する)という流れになっている。
理解するためには何が必要か?
異なる立場を表す文や引用を見つけたら、その後で筆者がどう切り返しているかを追う。
「どのような論拠・証拠」で再反論しているかに着目する。【文】難易度・論理構造の一覧表(2024-2013年)

実際の早稲田大学文学部でどのような問題が出たのかを見ていきましょう。
下記表は、早稲d大学文学部の要約問題の難易度論理構造を一覧にした表です。年度 テーマ 論理構造 難易度 2024年 Diversity in American Higher Education 対比(批判vs.実データ)+ 反論と再反論 [rating stars="4.0"] 2023年 Freud’s Two Conceptions of Reality 対比(2つの「現実」観)・矛盾構造 [rating stars="5.0"] 2022年 Accelerating Climate Change 因果(気候変動→極端気象) [rating stars="3.0"] 2021年 Speed-Reading vs. Slow-Reading 対比(速読vs.遅読)+部分的因果(速読→理解度低下) [rating stars="3.0"] 2020年 Memory, Forgetting, and Individual Identity 逆説(多くを忘れるのに自己は維持)+部分的な定義→例示 [rating stars="3.0"] 2019年 Social Identities and Public Representation 因果(社会的言説→アイデンティティ)+段階的拡大(個人→社会) [rating stars="4.0"] 2018年 English Literature as a Tool of Colonial Influence in India 目的と手段(植民地支配の効率化→英文学教育) [rating stars="3.0"] 2017年 Mozart & Salieri: A Case of Misrepresented History 対比(毒殺説vs.共作の新発見) [rating stars="2.0"] 2016年 Decline of External Moral Consensus in the U.S. 過去と現在の比較→変化(外部道徳→個人道徳) [rating stars="4.0"] 2015年 The Mass Microfilming Crisis in Libraries 問題-解決→逆説(マイクロフィルムが逆に劣化) [rating stars="3.0"] 2014年 The Rise of E-Books and the Possible End of Paper Books 対比(電子書籍vs.紙書籍) [rating stars="2.0"] 2013年 Urbanization: Global Population Shift to Cities 因果(都市化→農村衰退)+帰納的に統計→一般結論 [rating stars="2.0"] 難易度設定とその理由
2024年:難易度[rating stars="4.0"]
論理構造
対比(批判vs.実データ)+ 反論と再反論
理由
対比だけでなく「反論と再反論」が組み合わさり、筆者が「多様性の否定派」の意見を紹介してからデータで切り返すという流れを理解する必要がある。
特に、「多様性が既存の特権層の機会を奪うのでは」という批判をどう覆しているのか、事例や数値が示されている部分をしっかり追う必要があり、構造としてはやや複雑。
また、「多様性」と「民主主義」「拡大する入学定員」など社会的・政治的テーマに触れるため、背景知識・抽象的思考も要求される。2023年:難易度[rating stars="5.0"]
論理構造
対比(2つの「現実」観)・矛盾構造
理由
フロイトの理論という心理学・哲学的要素があり、「現実は心が作るもの」と「固定された外部の現実」という 概念自体が抽象的。
さらに両者が矛盾しているのに共存しているという、解決されない論理的対立を把握しなければならず、読解が難しい。
一般的な社会問題やデータによる説明よりも 思考実験や理論批評に近い 内容であり、読解にかなりの抽象的思考が求められる。
よって全12年分の中でも最も高めの難易度と判断2022年:難易度[rating stars="3.0"]
論理構造
因果(気候変動→極端気象)
理由
基本的には「気候変動が原因となり極端な天候が頻発する」というシンプルな因果関係を軸にしている。
ただし、具体的な災害例や将来的な悪化予測が登場し、「現在の非常事態が未来の通常になる」という少し ショッキングな表現 を理解する必要がある。
しかし、専門的な議論(化学的・物理的な仕組み)までは深掘りされず、メインは「因果」構造なので、難易度は中程度の「3」。2021年:難易度[rating stars="3.0"]
論理構造
対比(速読vs.遅読)+部分的因果(速読→理解度低下)
理由
「速読と遅読の対比」「読書速度が上がると理解度が下がる」という因果が主な軸。
文章自体のテーマ(読書法)も身近で、専門用語も少なめ。
一方で、「 comprehension と knowledge acquisition は違う」「メタ認知が必要」など、やや認知心理学的要素を理解する必要があるため、初心者には少し難しい部分も含む。
しかし全体としては読み取りやすく、難易度は中ぐらい。2020年:難易度[rating stars="3.0"]
論理構造
逆説(多くを忘れるのに自己は維持)+部分的な定義→例示
理由
「人間は多くを忘れるのになぜ自分でいられるのか」という逆説的なテーマを扱う。
記憶や脳の話なので、ある程度の生物学的・心理学的イメージがあると理解しやすい。
論理構造は「(A) 膨大に忘れる → (B) でもアイデンティティは維持 → (C) それは記憶の本質がこうだから」という比較的わかりやすいフロー。
逆説ではあるが、専門理論が多量に出るわけではなく、理解レベルとしては中くらいの難易度。2019年:難易度[rating stars="4.0"]
論理構造
因果(社会的言説→アイデンティティ)+段階的拡大(個人→社会)
理由
まず個人の行動が他者の言説にどう影響されるか、メディアによる集団イメージが社会政策にどう影響するか、などを 段階的に拡大 して解説している。
「社会構築主義」「ステレオタイプ」「内面化」など、社会学・心理学の概念を背景に読む必要がある。
因果関係が多層的(「他者の表象 → 集団アイデンティティ形成 → 政策反映 → 当事者がさらに内面化」)でやや複雑。
そのため「4」というやや高めの難易度に設定。2018年:難易度[rating stars="3.0"]
論理構造
目的と手段(植民地支配の効率化→英文学教育)
理由
「植民地行政の都合でインド人をどのように支配下に置こうとしたのか」が主題で、 歴史的事実とその目的 → 手段 というわかりやすい流れ。
キリスト教布教との対比などもあるが、構造としては単純で、読み慣れれば理解しやすい。
歴史や植民地主義などの背景知識があれば、難解さはさほど高くないため「3」。2017年:難易度[rating stars="2.0"]
論理構造
対比(毒殺説vs.共作の新発見)
理由
「モーツァルトとサリエリの有名な毒殺説」と「実際の史料発見(共作)」を対比するシンプルな構造。
結論として「歴史の定説が覆った」という話なので、難しい理論や複雑な論理展開はない。
文化史的知識が多少あると理解しやすく、比較的読みやすい題材。
よって「2」という低めの難易度。2016年:難易度[rating stars="4.0"]
論理構造
過去と現在の比較→変化(外部道徳→個人道徳)
理由
「昔は外部の道徳観に従っていたが、今は個人の内面を重視するようになった」という 社会通念や倫理観の変化 がテーマ。
「道徳秩序」「内面の自己」「解放や自立」といった倫理社会学的要素が含まれ、やや抽象度がある。
1960年代のアメリカ文化・社会の背景がわかるとスムーズだが、そうでないと少し難しく感じる。
そのため「4」。2015年:難易度[rating stars="3.0"]
論理構造
問題-解決→逆説(マイクロフィルムが逆に劣化)
理由
「書架不足&酸性紙劣化という問題 → マイクロフィルム化 → 逆にフィルムも劣化する」という 問題→解決策→逆説 の典型構造。
大規模に本を裁断・廃棄したのにフィルムもダメだった、という皮肉な結末を抑えればよいので、非常に明快。
ただ、図書館運営の知識が全くないと少し背景説明が必要になるかもしれないが、文章構成としてはシンプルなので「3」。2014年:難易度[rating stars="2.0"]
論理構造
対比(電子書籍vs.紙書籍)
理由
「電子書籍のメリット vs. 紙の本の良さ」という身近な話題の対比で、比較的とっつきやすい。
専門的な数字や理論もなく、テクノロジーや読書経験があれば理解しやすいので難易度は低め。
「将来は紙の本がなくなるかも?」という結論もわかりやすい。2013年:難易度[rating stars="2.0"]
論理構造
因果(都市化→農村衰退)+帰納的に統計→一般結論
理由
「2008年に都市居住人口が過半数に」「農村は若者の流出で衰退」という 因果関係 を示す。
具体的な統計(UNのデータ)→一般化(世界的傾向)という構造が読みやすい。
テーマもグローバル化・都市化というわかりやすい社会現象で、背景知識がなくても比較的理解しやすいので「2」。【文化構想】難易度・論理構造の一覧表(2024-2013年)

実際の早稲田大学文化構想学部でどのような問題が出たのかを見ていきましょう。
下記表は、早稲田大学文化構想学部の要約問題の難易度論理構造を一覧にした表です。年度 テーマ 論理構造 難易度 2024年 芸術と知識は「直接的価値」か「間接的価値」か 対比(芸術=直接的幸福手段 vs. 知識=間接的手段)+「文明人の価値意識」 [rating stars="4.0"] 2023年 “エスキモーは雪を表す単語が多数ある”という誤情報とその拡散 対比(真実 vs. 面白がられる神話)+皮肉(学術界でも広まる誤情報) [rating stars="3.0"] 2022年 ロックダウンで拡張するデジタル世界と「ハイパーリアリティ」 因果(ロックダウン → オンライン依存激化)+「習慣の大転換」 [rating stars="3.0"] 2021年 「コミュニケーション」はメッセージ伝達だけでなく、役割演技・儀礼行為でもある 定義+対比(送信モデル vs. 儀礼モデル)+社会的役割のパフォーマンス [rating stars="3.0"] 2020年 近現代の英国スポーツ文化の変容とメディア・市場の影響 過去と現在の比較(道徳的体育 → 商業的・消費主義的スポーツ) [rating stars="4.0"] 2019年 産業資本主義と労働時間の変化:時計がもたらした効率化と「時間の売買」 因果(時計導入→労働管理)+逆説(人間が“時間”を売るようになる) [rating stars="3.0"] 2018年 教育の社会化機能とそのパラドックス 対比(社会への順応 vs. 社会変革)+逆説(社会化がかえって批判意識を生む) [rating stars="3.0"] 2017年 予想を超えた「新しいコミュニケーション様式」と人間の欲望の限界 比較(SFの想像力 vs. 実際の技術進歩)+新たに「作られる」欲望 [rating stars="2.0"] 2016年 「会話」はゴール設定のない活動であり、むしろ互いに“導かれる”もの 対比(議論=勝敗あり vs. 会話=勝敗なし)+引用(ガダマーの会話論) [rating stars="3.0"] 2015年 海外生活からの帰国時にも起こる「カルチャーショック第2波」 問題提起(帰国者もショックを受ける)+原因(周囲の無関心・環境変化) [rating stars="2.0"] 2014年 「五感」以外に存在する人間の感覚とは? 定義の拡張(第六感=超常?→実は他にも身体感覚・内的感覚がある) [rating stars="2.0"] 2013年 ARPANETから生まれたインターネットは誰の所有物でもないが、規制の動きもある 歴史的経緯(政府の研究→世界的ネット)+対比(自由な協働 vs. 各国規制) [rating stars="2.0"] 難易度設定とその理由
2024年:難易度[rating stars="4.0"]
論理構造
芸術は“作品を鑑賞すれば直接的に優れた感情状態を得られる”
知識は“いったん内面で咀嚼されてはじめて価値をもつ(間接的な手段)”
真に「文明的」な人は、その知識の持つ精神的価値(実用性ではなく)を重んじる難易度理由
一見すると芸術の直接価値と知識の間接価値を比べるだけだが、「文明人が知識をどう扱うか」という抽象的な価値観まで踏み込むため、やや哲学色が強い。
「直接手段 vs. 間接手段」「最終的には同じ“精神的充実”をもたらす」など二重構造の理解が必要で、難易度はやや高めの「4」。2023年:難易度[rating stars="3.0"]
論理構造
一般大衆は「面白い話」を一度受け入れると撤回しにくい
学術界ですら誤情報を批判的検証なしに定着させることがある
代表例=エスキモーの語彙説(実は全く文献根拠がない)難易度理由
内容自体は「誤情報が広まる例」としてシンプル。
ただし「学問コミュニティまでミスを踏襲する皮肉」という構造理解が重要。抽象度はそこまで高くないため、難易度は中程度の「3」。2022年:難易度[rating stars="3.0"]
論理構造
ロックダウンが世界的規模で人々をオンライン生活へ押しやった
それ自体は既存テクノロジー(Zoom, Twitch, Amazonなど)が引き金
重要なのは“テクノロジーが変わったのではなく、人間の関わり方が激変した”点難易度理由
「社会実験としてのロックダウン」「既存技術+人間の習慣転換」という因果関係を追う必要あり。
しかし扱う要素は比較的具体的かつ身近で、背景知識もそこまで難しくないので「3」。2021年:難易度[rating stars="3.0"]
論理構造
人は相手・状況に応じて自己を演じ分ける(複数の“誠実な自分”)
SNS投稿なども、“実際の受け手”というよりは“周囲へのパフォーマンス”
送信モデル (sender-message-receiver) ではなく、儀礼モデル(役割・社会構造の再確認)で捉える解説・難易度理由
自分が“母親”を演じる投稿の例を通して、投稿内容が「実際の相手」ではなく「想定された第三者」向けであるという点がやや抽象的。
ただし社会学的な文脈がある程度わかれば読みやすいため、中間レベルの「3」。2020年:難易度[rating stars="3.0"]
論理構造
19世紀、上流階級の学校でスポーツは“品性・道徳”を鍛える手段とされた
20世紀後半以降、メディアの発展・商業主義がスポーツ組織の在り方を変容させる
結果として“金銭・市場”によるスポーツ運営が主流化し、従来のアマチュア精神は崩壊難易度理由
歴史的背景(英国パブリックスクール~帝国主義の名残)と、メディア・企業参入によるビジネス化という二重の流れを追う必要がある。
社会・経済・歴史の複合理解が要り、難易度はやや高めの「4」。2019年:難易度[rating stars="3.0"]
論理構造
伝統的農村社会では“自然のリズム”が時間の基準
工場制・時計導入により、労働時間管理が個人から切り離される人は“時間を売る”存在となり、効率・生産性が重視される世の中へ難易度理由
比較的わかりやすい因果関係(時計=工場労働=時間管理)で進む。
「時間が貨幣化する」点が重要だが、具体例も多く抽象概念はそこまで難しくないため「3」。2018年:難易度[rating stars="3.0"]
論理構造
教育の目的:社会の価値観や規範を身につけさせる(社会化)
しかしJames Baldwinの言うとおり、教育を受けるほど社会を批判的に見る力も生まれる
結果として“社会へ順応”と“社会への批判”が同時に起こる可能性難易度理由
「社会化の道具が逆に社会批判を育む」という逆説を理解する必要がある。
テーマ自体は教育論でとっつきやすいが、抽象思考が若干必要なので「3」。2017年:難易度[rating stars="2.0"]
論理構造
過去のSFでは“ビデオ電話”などは予測されたが、携帯端末でどこでも……は描き切れなかった
そもそも“世界に向けてつぶやく”欲望自体、昔の人は持っていなかった
テクノロジーが進歩し、新たな欲望が次々と“創出”されている難易度理由
「人間の想像力の限界」という視点と「新たな欲望の創造」という発想がメイン。
概念自体は難しくなく、読みやすいため「2」。2016年:難易度[rating stars="3.0"]
論理構造
議論(Argument)とは異なり、会話には勝ち負けや明確なゴールがない
ガダマーの言うように、参加者はむしろ会話に“導かれる”
他者の発話内容が少しずつズレても、それを含めて楽しむのが会話難易度理由
「会話の終了条件は外部要因のみ」「コントロールしようとすれば破綻する」などがキー。
ガダマー哲学がちらりと出るが、大きく深入りはしないため中程度の「3」。2015年:難易度[rating stars="2.0"]
論理構造
海外でのカルチャーショックは有名だが、帰国後に再びショックが起こることがある
家族・友人が海外経験にあまり興味を示さない→疎外感
本人が環境の変化に追いつかず“帰りたい”と思う場合も…難易度理由
理解しやすいエピソード的内容。抽象理論や専門用語も少ない。
「2」という低めの難易度。2014年:難易度[rating stars="2.0"]
論理構造
アリストテレス以来の“五感”という前提
しかし“階段を何段上がるか”など身体位置感覚はどこに分類?
吐き気や疲労感などは五感では説明できない難易度理由
身体感覚の話なので、具体例(階段、タイプ入力など)が分かりやすい。
学術的には“固有受容感覚”や“内臓感覚”という領域だが、本文も難解ではなく「2」。2013年:難易度[rating stars="2.0"]
難易度理由
歴史的背景も短くまとめられており、基本的には読みやすい。
インターネット管理の仕組みをざっくり知っていれば理解しやすく、「2」。早稲田文・文化構想で出題されそうな論理構造の予測4パターン
ここまでの内容を踏まえてヒロアカでは早稲田大学文学部、文化構想学部で今後出そうな問題の論理構造を予測しました。
苦手なタイプの論理構造があれば、
英文もセットで載せておくので理解をしておくと良いでしょう。【頻出】 パターン1:依然として「対比構造」が軸!
2024年を含め多くの回で「A vs. B」という二項対立が組み込まれてきています。
したがって、2025年も何らかの「AとBの対立や比較」を扱い、
最終的に筆者の立場を示すか、もしくは両者が実は両立できるという展開が来る可能性は高いです。対比構造を使った英文を用意してみました。
The Rise of Digital Nomads: Flexibility vs. Stability
In recent years, the notion of working and traveling simultaneously has gained significant popularity, giving birth to a new breed of professionals known as “digital nomads.” Proponents argue that this lifestyle offers unparalleled freedom, allowing individuals to explore diverse cultures while maintaining a career on their own terms. They point out that remote work eliminates long commutes and fosters creativity through constant exposure to fresh environments. However, critics question the viability of this wanderlust-driven approach. They emphasize that a stable work setting often promotes stronger social connections, professional development, and consistent routines. Unlike digital nomads, office-based employees can readily seek advice from seasoned mentors, cultivate enduring professional networks, and benefit from clear corporate structures.Ultimately, the debate hinges on whether the thrill of mobility outweighs the potential drawbacks of limited job security and fragmented relationships. Although digital nomadism promises a life of adventure, skeptics warn that its short-term excitement may not guarantee long-term career growth or personal stability.構造の特徴: “Flexibility vs. Stability” という二項対立を明示し、前半で「自由・創造性」を肯定、後半で「安定と継続的成長の大切さ」を否定的観点から示しています。
筆者の立場: 明言しすぎずに双方のメリット・デメリットを列挙し、最後に「トレードオフ」を示す形でまとめています。実際の出題では、最終段落でどちらに重心があるかを要約で問われることが多いです。パターン2:社会問題・新たなテクノロジーに関する「問題-解決」パターン
大学入試の題材としては、気候変動やAI、デジタル化など「現代的テーマ」は引き続き扱われやすい。
すでに電子書籍(2014年)やマイクロフィルム問題(2015年)といった「情報管理」系の話題があったので、AI活用・ビッグデータ・デジタル・オンライン教育などを絡めて「問題提示 → 解決策や方向性」を示すような論理構造が出ても不思議ではありません。Addressing Algorithmic Bias in Online Recruitment
As more companies adopt automated systems to screen job applicants, a growing concern is the potential for algorithmic bias to exclude qualified candidates. These biases often arise when the historical data used to train the algorithms reflect existing inequalities, such as underrepresentation of certain ethnic groups or gender stereotypes. Consequently, well-intentioned recruiters may unknowingly miss out on diverse talent, while perpetuating systemic discrimination.
To combat this issue, experts recommend several strategies. First, organizations should regularly audit the data sets and screening criteria to identify patterns of bias. Second, companies can employ diverse development teams, ensuring that the people designing these algorithms are sensitive to various cultural and social contexts. Finally, transparency in how the software makes its decisions allows both applicants and regulators to hold employers accountable. Through these measures, automated hiring practices can become more equitable, benefiting both job seekers and forward-thinking businesses alike.構造の特徴: 前半で「問題提起(algorithmic bias)」を明確に述べ、後半で「解決策(複数の具体的ステップ)」を列挙する流れ。
読解の要点: どのような問題か、どう対処しようとしているかを把握するのがポイント。要約問題では「なぜバイアスが生じるのか」「その対策は何か」を整理することが重要です。パターン3:「逆説・パラドックス」的な要素を含む人文系トピック
2020年の記憶と忘却や、2023年のフロイトの事例のように、「一見矛盾するが両方成り立つ」視点を深く掘り下げる文章も定番です。
人間の行動・認知科学・心理学などで「AかBかと思いきや、実は両方必要/両立している」ようなテーマが引き続き登場するかもしれません。The Productivity Paradox: Working Less to Achieve More
It seems contradictory to suggest that people might produce higher-quality work by reducing their total working hours. Yet recent studies have shown that shorter workweeks can actually lead to increased productivity, reduced stress, and greater job satisfaction. On the surface, it appears illogical: how can working fewer hours result in accomplishing more tasks?
One explanation lies in the concept of “focused energy.” When employees know they have limited time, they often eliminate unproductive activities and concentrate on the most crucial tasks. This heightened focus can intensify creativity and reduce burnout, enabling teams to achieve better outcomes within tighter schedules. Meanwhile, free time away from work fosters mental recovery, allowing for deeper problem-solving and innovative thinking.
Paradoxically, by constraining work hours, organizations may cultivate an environment where both individuals and projects flourish—a notion that challenges the age-old belief in endless labor as the path to progress.構造の特徴: 一見「労働時間を減らす」ことと「生産性が上がる」ことは矛盾(パラドックス)に見えますが、実は両立し得るという逆説を示しています。
読解の要点: 「従来の常識を覆す要素は何か」「どのような仕組みで両立するのか」が焦点。要約問題では原因や理由を明示してまとめるとよいでしょう。パターン4:社会構造の変化・歴史解釈の変遷などをめぐる「相互作用」や「対立構造」
近年の例では、サリエリとモーツァルト、植民地支配と英文学など「歴史解釈の変化」もテーマ化されてきました。
歴史的事件や人物の再評価、昔の認識と現代の研究結果との食い違いなどを扱う文章が再度出ることも考えられます。Reevaluating Queen Isabella: Conqueror or Visionary?
Historians have long portrayed Queen Isabella of Castile as a staunch advocate of imperial expansion, often criticizing her for the harsh treatment of indigenous peoples under Spanish rule. Traditional accounts emphasize her relentless drive for power, highlighting her role in sponsoring overseas conquests and consolidating absolute authority. In recent years, however, scholars have begun to reassess her reign by examining newly discovered letters and financial records.
These sources suggest that Isabella was more than a ruthless conqueror; she also championed administrative reforms and education initiatives that laid the groundwork for Spain’s subsequent cultural renaissance. Moreover, her personal correspondence reveals concerns about the moral implications of colonization and the potential for cultural exchange. While modern perspectives cannot entirely absolve Isabella of wrongdoing, they do paint a more nuanced portrait of a ruler grappling with the complexities of nation-building. In this light, Isabella’s legacy may be neither purely heroic nor wholly villainous, but a blend of both.構造の特徴: 従来の歴史解釈(“ruthless conqueror”)と新たな資料による再評価(“more nuanced portrait”)の対比・変化を示しています。
読解の要点: どこが従来と異なる評価か、また新資料によってどう見方が変わったのかが文章のメインテーマ。入試で問われやすいのは、「旧来説と新説の違い」「筆者がどうまとめているか(完全肯定・完全否定ではなく“blend of both”)」といった部分です。早稲田文学部・文化構想のどの過去問から対策をしたら良いのか?
再度難易度をまとめなおしました。
中間レベルの問題が一般的なのでまずはこのレベルの問題を解いてみて、
話の内容をどの程度理解することができてまとめることができるのかを考えてみましょう。難易度 [rating stars="2.0"](比較的易しめ)
2017 文学部:Mozart & Salieri: A Case of Misrepresented History
2014 文学部:The Rise of E-Books and the Possible End of Paper Books
2013 文学部:Urbanization: Global Population Shift to Cities
2017 文化構想学部:New Communication Types Surpassing SF Imagination
2015 文化構想学部:Reverse Culture Shock upon Returning Home
2014 文化構想学部:Beyond the Five Senses
2013 文化構想学部:ARPANET and the Future of the Internet難易度 [rating stars="3.0"](中間レベル)
2022 文学部:Accelerating Climate Change
2021 文学部:Speed-Reading vs. Slow-Reading
2020 文学部:Memory, Forgetting, and Individual Identity
2018 文学部:English Literature as a Tool of Colonial Influence in India
2015 文学部:The Mass Microfilming Crisis in Libraries
2023 文化構想学部:“Eskimos Have Many Words for Snow” as a Common Myth
2022 文化構想学部:Hyperreality and Our Shift to the Online World
2021 文化構想学部:Communication as Performance and Ritual
2019 文化構想学部:Clock Time and Industrial Capitalism
2018 文化構想学部:Education’s Paradox: Socialization vs. Critical Awareness
2016 文化構想学部:Conversation as a Goal-Free Activity難易度 [rating stars="4.0"](やや難)
2024 文学部:Diversity in American Higher Education
2019 文学部:Social Identities and Public Representation
2016 文学部:Decline of External Moral Consensus in the U.S.
2020 文化構想学部:Transformation of Sports in Modern Britain
2024 文化構想学部:Art vs. Knowledge: Direct vs. Indirect Means to Good難易度 [rating stars="5.0"](最も難解)
2023 文学部:Freud’s Two Conceptions of Reality
英検2級、準1級レベルの単語をアウトプットレベルに
読解ができればあとは、自分の言葉で言い換えるだけなので難しくはありません。
確かに自分の言葉で言い換えるのなんて無理・・と思いがちですが、
読解が成功していれば、どこを書けば良いのかがわかるわけですから、
何を書いたら良いのか?について理解するのは難しくありません。できれば受験までに英検2級、準1級を受けて、
合格水準のライティング力をつけておくと良いでしょう。ヒロアカで早稲田文学部、文化構想学部の対策を完璧に!

ヒロアカでは早慶専門塾として0から早稲田大学文学部、
文化構想学部の対策ができるようにしています。
要約問題の対策はもちろんのこと、それ以外の対策も自信を持って解答ができるレベルまで指導をしています。
お気軽にご相談ください。






















