2017年慶應義塾大学総合政策|過去問徹底研究 大問3 方針の立て方 (1) 文字が3つと多いため,典型的な一文字固定法で考えていくのが妥当. (2) 前問の結果から,のときが答えだと当たりをつけて考えていく.のときに使える多変数の公式といえば,相加相乗平均の関係式であるから,試しに使ってみると,解
- …続きを読む
-
2017年慶應義塾大学総合政策|過去問徹底研究 大問3
方針の立て方
(1)
文字が3つと多いため,典型的な一文字固定法で考えていくのが妥当.(2)
前問の結果から, のときが答えだと当たりをつけて考えていく.
のときが答えだと当たりをつけて考えていく. のときに使える多変数の公式といえば,相加相乗平均の関係式であるから,試しに使ってみると,解法を得る.
のときに使える多変数の公式といえば,相加相乗平均の関係式であるから,試しに使ってみると,解法を得る.解答例
(21)(22)(23)(24)(25)(26)……

(27)(28)(29)(30)(31)(32)(33)(34)……
解説
(1)
AB ,AD
,AD ,AE
,AE とおく.すると,
とおく.すると,
条件式: となる.
となる.
 より,
より, である.
である.
体積は,

不等号の等号成立条件は である.
である.
ここで, とおくと,
とおくと,
増減表を描くと,

















よって,

ここで,

となる.このとき, となり,これらは全て適当である.
となり,これらは全て適当である.
よって,
 ……(答)
……(答)(2)
AB ,AD
,AD ,AE
,AE とおく.すると,
とおく.すると,
条件式: となる.
となる.
ここで,相加相乗平均の関係式
![Rendered by QuickLaTeX.com x+y+z\geqq3\sqrt[3]{xyz}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAJ4AAAAUAQAAAABU1bloAAAAAnRSTlMAAHaTzTgAAAANSURBVBgZYxgFgx4AAAGkAAFxBV+vAAAAAElFTkSuQmCC) (等号成立は
(等号成立は のとき)
のとき)
であり,
 (等号成立は
(等号成立は のとき)
のとき)
 (等号成立は
(等号成立は のとき)
のとき)
 (等号成立は
(等号成立は のとき)
のとき)
であり,
![Rendered by QuickLaTeX.com \sqrt{2xy}+\sqrt{2yz}+\sqrt{2zx}\geqq3\sqrt[3]{\sqrt{2xy}\cdot\sqrt{2yz}\cdot\sqrt{2zx}}=3\sqrt2\cdot\sqrt[3]{xyz}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAgYAAAAiAQAAAAAM5iwEAAAAAnRSTlMAAHaTzTgAAAAYSURBVBgZYxgFo2AUjIJRMApGwSgYggAACMQAAcLyBrwAAAAASUVORK5CYII=) (等号成立は
(等号成立は のとき)
のとき)
であることを用いると,
![Rendered by QuickLaTeX.com 1=x+y+z+\sqrt{x^2+y^2}+\sqrt{y^2+z^2}+\sqrt{z^2+x^2}\geqq3\sqrt[3]{xyz}+\sqrt{2xy}+\sqrt{2yz}+\sqrt{2zx}\geqq3\sqrt[3]{xyz}+3\sqrt2\cdot\sqrt[3]{xyz}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmgAAAAxAQAAAABGimjyAAAAAnRSTlMAAHaTzTgAAAAaSURBVEjH7cEBDQAAAMKg909tDwcUAAAAvBkO7gABtBf6SAAAAABJRU5ErkJggg==)
が成り立つ.等号成立は のときであり,最左辺と最右辺に着目すると,
のときであり,最左辺と最右辺に着目すると,
![Rendered by QuickLaTeX.com \sqrt[3]{xyz}\leqq\frac{1}{3+3\sqrt2}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAHYAAAAcAQAAAACcs3aAAAAAAnRSTlMAAHaTzTgAAAANSURBVBgZYxgFQxoAAAHAAAGwMl93AAAAAElFTkSuQmCC)

となる. は考えている直方体の体積であることに注意されたい.
は考えている直方体の体積であることに注意されたい.
さて, のとき,条件式より,
のとき,条件式より, となり,
となり, となる.これは適当である.よって,
となる.これは適当である.よって,
 ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。







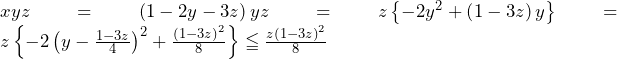
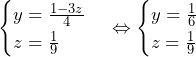

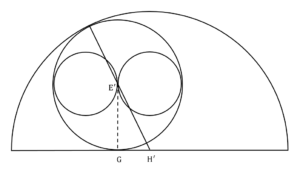
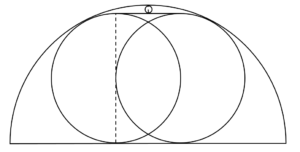
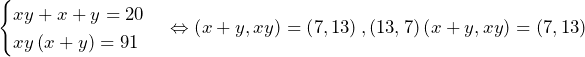 について.
について.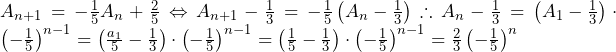
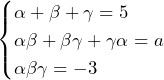
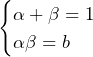
 ……(答)
……(答)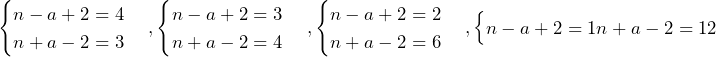
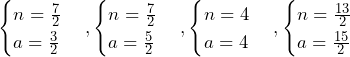
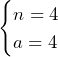 のみ.これより,答えは,
のみ.これより,答えは,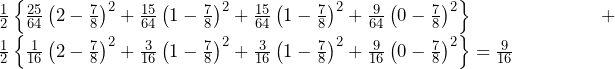 ……(答)
……(答)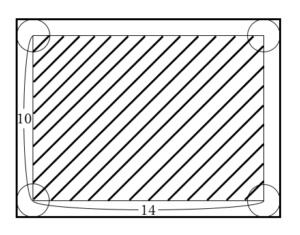
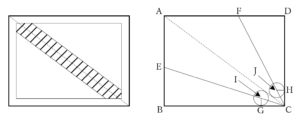
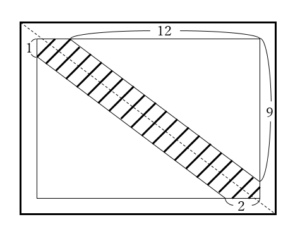
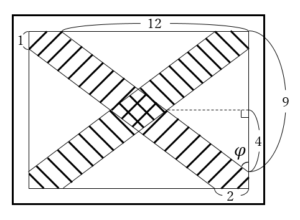


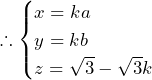
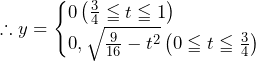 で
で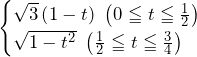
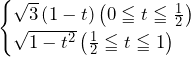
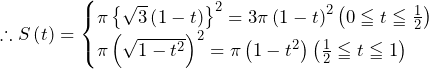 ……(答)
……(答)![Rendered by QuickLaTeX.com V=\int_{0}^{1}S\left(t\right)dt=\int_{0}^{\frac{1}{2}}{3\pi\left(1-t\right)^2}dt+\int_{\frac{1}{2}}^{1}\pi\left(1-t^2\right)dt=\left[-\pi\left(1-t\right)^3\right]_0^{\frac{1}{2}}+\left[\pi\left(t-\frac{1}{3}t^3\right)\right]_{\frac{1}{2}}^1=\frac{13}{12}\pi](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-23dadfd7a2f6b605eb35cb7bc70d9990_l3.png) ……(答)
……(答)