早稲田大学教育学部
理系数学なので当たり前なのですが、数学Ⅲの微分積分をテーマとした問題が、毎年出題されています。
その他の分野では、数列、漸化式、確率、場合の数、といった分野も頻出となっています。
圧勝している人はこう考える
ここでは過去問を使って、早慶の入試で圧勝をしている人はどのように考えているのかを示していきます。

(1)は簡単ですが、少し実験して考えてみましょう。
実験
 ここくらいまで考えれば、状況がつかめてきますね!
ここくらいまで考えれば、状況がつかめてきますね!
・n秒後に外の囲い(■)が点灯すること。
・3囲いずつ点灯と消灯をくり返すこと。(周期が3)
ここまでつかめば、こっちのものです。
記述するにおいて、上のように”・”をたくさん書くのは面倒ですし、厳密な答案を書く上で少し工夫してみましょう。
n=1で点灯した電球を原点(0,0)として、電球を座標平面上の格子点に載せてみます。
解 電球を座標平面上の格子点にのせて、最初に点灯した電球を原点(0,0)にもってくる。

(1)n+1秒後に初めて点灯した電球はn秒後に点灯した電球と隣接しているから![]() =1or
=1or![]() である。
である。
(![]() はk秒後にはじめて点灯した電球)(n≧1)
はk秒後にはじめて点灯した電球)(n≧1)
∴n秒後に初めて点灯する電球の個数![]() は|x|=n-1かつ|y|=n-1かつ|x|≦n-1,|y|≦n-1を満たす格子点の個数に一対一に対応する。
は|x|=n-1かつ|y|=n-1かつ|x|≦n-1,|y|≦n-1を満たす格子点の個数に一対一に対応する。
![]() =4{2(n-1)+1}-4=8(n-1)(n≧1)
=4{2(n-1)+1}-4=8(n-1)(n≧1)
以上からまとめると![]() ,
,![]() =8(n-1)(n≧2)…(答)
=8(n-1)(n≧2)…(答)
(2)消える電球を無視して考えると、n秒後についている電球の個数![]() は1辺が(2n-1)の正方形の面積と対応するから、
は1辺が(2n-1)の正方形の面積と対応するから、![]() …①
…①
ここから、周期3ごとに消灯する電球を引いて考える。
(ⅰ)n=3k+1(k≧1)のとき、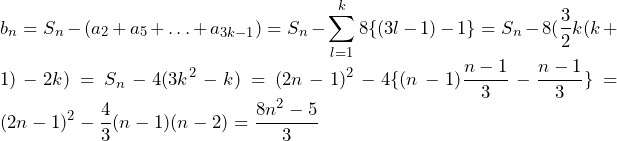 …(答)(n=1のときも成立)
…(答)(n=1のときも成立)
(ⅱ)n=3k+2(k≧2)
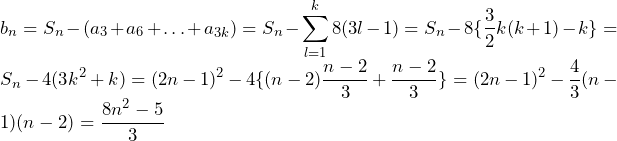 …(答)(n=2のときも成り立つ。)
…(答)(n=2のときも成り立つ。)
(ⅲ)n=3(k+1)(k≧1)
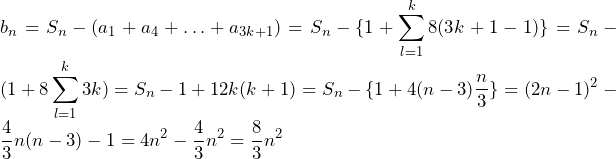 …(答)
…(答)
(3)(2)より
(ⅰ)(ⅱ)のとき、![]()
(ⅲ)のとき、![]()
なので、![]() …(答)
…(答)
■(3)を少し考えてみましょう。
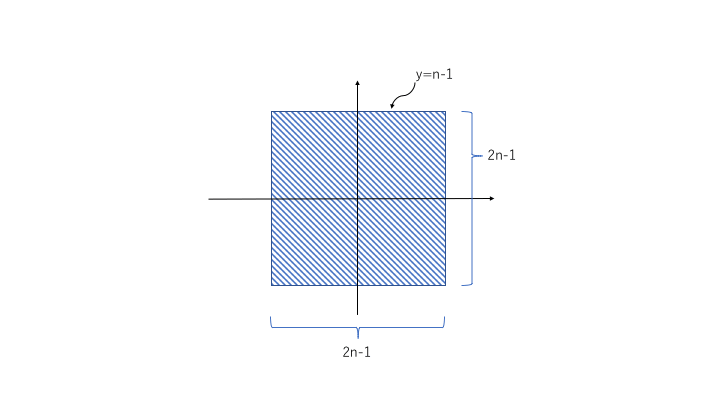
![]() とは(2)の通り左図の斜線の面積で
とは(2)の通り左図の斜線の面積で![]() は、左図でいう約第一象限分の面積ですから、
は、左図でいう約第一象限分の面積ですから、![]() です。
です。
![]() (消灯分の面積)なので、
(消灯分の面積)なので、![]()
![]()
![]() をXとすると、
をXとすると、
![]() で
で
![]() がわかります。
がわかります。
原点に点がついたときは、点灯している面積のほうが断然大きくなりますが、nが十分大きくなると(消灯分の面積):(点灯分の面積)=1:2となっていくわけですね。
一人ひとりの節電が地球を救います!Let’s省エネ!
(問)nを2以上の自然数とし1からnまでの自然数の順列:![]() のうち条件(※)を満たす順列の個数を
のうち条件(※)を満たす順列の個数を![]() とおく。
とおく。
条件(※):![]() を満たさないようなkが順列中にただ1つ存在する。
を満たさないようなkが順列中にただ1つ存在する。
以下の問いに答えよ。
(1)![]() を求めよ。
を求めよ。
(2)![]() を求めよ。
を求めよ。
(3)![]() を
を![]() を用いて表わせ。
を用いて表わせ。
(4)![]() をnを用いて表わせ。 (2017早大教育1(2)改題)
をnを用いて表わせ。 (2017早大教育1(2)改題)
少し解きやすく改題してみました。早速やってみましょう。
実験 ![]() に適する順列を( ),適さないものを{ }で表します。
に適する順列を( ),適さないものを{ }で表します。
(表)
あとは各々の補題(ⅰ)(ⅱ)を示して(3)を先に解いてしまいます。
[(ⅰ)の証明]nを大きな数とする。![]() のある順列について、(
のある順列について、(![]() )が(※)と条件を満たすとする。(
)が(※)と条件を満たすとする。(![]() )
)
ここに(n+1)を挿入することを考える。
(Ⅰ)![]() について、
について、![]() (1≦j≦i)はすべてn以下なので、この↑のうち1つに(n+1)を挿入すると
(1≦j≦i)はすべてn以下なので、この↑のうち1つに(n+1)を挿入すると![]() を満たさないところがこの順列だけで1か所存在してしまい、
を満たさないところがこの順列だけで1か所存在してしまい、![]() と合わせて2か所存在するので、(※)に反する。
と合わせて2か所存在するので、(※)に反する。
(Ⅱ)いま、![]() かつ
かつ![]() なので(※)を満たす順列が作れる。
なので(※)を満たす順列が作れる。
(Ⅲ)(Ⅰ)と同様に不適。
(Ⅳ)![]() であるから(※)を満たす順列が作れる。
であるから(※)を満たす順列が作れる。
以上、(Ⅰ)〜(Ⅳ)から(ⅰ)は示される。
[(ⅱ)の証明]いま、↑のnコに(n+1)を挿入すれば、![]() を満たすところが1ヶ所だけ存在する。(nコのうしろに挿入すると、{1,2,…n,n+1}となり(※)に不適)
を満たすところが1ヶ所だけ存在する。(nコのうしろに挿入すると、{1,2,…n,n+1}となり(※)に不適)
(1,2,3,…n)の元の並びから、(ⅰ)と(ⅱ)は互いに排反である。
以上から、![]() …(答(3))が導けました。
…(答(3))が導けました。
(![]() =4,
=4,![]() =2・4+3=11)
=2・4+3=11)
(4)さて、![]() …①を解いてみましょう。
…①を解いてみましょう。
①⇄![]()
![]() とおく。
とおく。![]()
(![]() )より
)より![]()
∴![]() …(答)となります。
…(答)となります。
どうでしたか?実験の重要性をわかって頂けましたか?
ただ覚えるだけの数学だけではなく、考えて数学を勉強していきましょうー!
早稲田大学 教育学部に圧倒的な実力で合格できる専門対策をします
まずは資料請求・お問い合わせ・学習相談から!
早慶専門個別指導塾HIRO ACADEMIAには、早稲田大学専門として教育学部への圧倒的な合格ノウハウがございます。
少しでもご興味をお持ちいただいた方は、まずは合格に役立つノウハウや情報を、詰め込んだ資料をご請求ください。
また、早稲田大学教育学部に合格するためにどのよう勉強をしたらよいのかを指示する学習カウンセリングも承っています。学習状況を伺った上で、残りの期間でどう受かるかを提案いたしますので、ぜひお気軽にお電話いただければと思います。
⇒ 早稲田大学・教育学部に合格したい方は、まずは当塾の資料をご請求ください。
















Published by