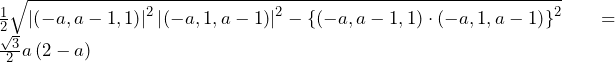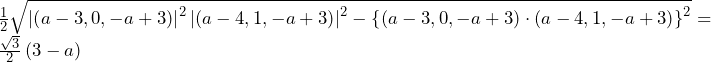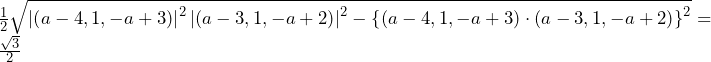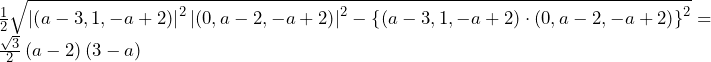方針の立て方 (1) 絶対値問題の典型的解法,つまり,場合分けをして絶対値記号を外すことを試みる.その後は二次関数の最大最小問題と同じように,区間とグラフの位置関係で場合分けを行う.場合分けのパターンが多いが,対称性があるため⑤~⑦は実質的に計算しなくても答えは分かる.後はと直線を図示して面積を求め
- …続きを読む
- 方針の立て方
(1)
絶対値問題の典型的解法,つまり,場合分けをして絶対値記号を外すことを試みる.その後は二次関数の最大最小問題と同じように,区間とグラフの位置関係で場合分けを行う.場合分けのパターンが多いが,対称性があるため⑤~⑦は実質的に計算しなくても答えは分かる.後は と直線
と直線 を図示して面積を求めるのみ.
を図示して面積を求めるのみ.
(2)
4次方程式の解析は難しいため,次数を下げることを考える.そこで「 は代数方程式
は代数方程式 の解である」⇔「多項式
の解である」⇔「多項式 は
は を因数にもつ」という解の重要性質を利用すると考えよう.この重要性質を使えば,2次方程式の解析問題に帰着させられる.後は,実数解なのか虚数解なのかで場合分けをして考えればよい.
を因数にもつ」という解の重要性質を利用すると考えよう.この重要性質を使えば,2次方程式の解析問題に帰着させられる.後は,実数解なのか虚数解なのかで場合分けをして考えればよい.(3)
長さの問題であるため,座標系を導入すると考えやすくなると考える.「座標は長さの問題のときに強く,角度の問題のときには弱い」というのは覚えておこう.後は問題の状況を丁寧に書き下していけばよい.平方完成を用いた最小値問題は頻出問題なのでおさえておくこと.(4)
 と
と のどちらが
のどちらが の値になるかを考えよう(絶対値記号と同様に
の値になるかを考えよう(絶対値記号と同様に もそのままでは扱いにくいので外すことをまず考える).「全ての整数
もそのままでは扱いにくいので外すことをまず考える).「全ての整数 に対して」となっているので,まずは
に対して」となっているので,まずは を固定して
を固定して のみを変数扱いして考えよう.
のみを変数扱いして考えよう. と
と はそれぞれ単調増加,単調減少であるため,最初は
はそれぞれ単調増加,単調減少であるため,最初は となるだろうと分かる.そこで
となるだろうと分かる.そこで となる
となる を考える.後は十分条件を考え,そのあとで,必要性を考える.つまり,
を考える.後は十分条件を考え,そのあとで,必要性を考える.つまり, は言えるが,では
は言えるが,では をこれより大きくした場合はどうか,具体的には
をこれより大きくした場合はどうか,具体的には はどうかを考える必要があると考える.すると
はどうかを考える必要があると考える.すると で(*)を満たさないことが確認できるので,答えは63と分かる.
で(*)を満たさないことが確認できるので,答えは63と分かる.解答例
(1)
ア:
(2)
イ:
ウ:
(3)
エ:
(4)
オ:
解説
(1)
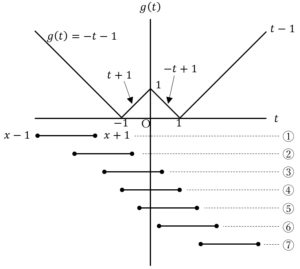
 とおくと,
とおくと,

①のとき( )
)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{x+1}\left(-t-1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2-t\right]_{x-1}^{x+1}=-x-1](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAb4AAAAcAQAAAAA2VecVAAAAAnRSTlMAAHaTzTgAAAAUSURBVBgZYxgFo2AUjIJRMApIBAAGPAABiiN6VQAAAABJRU5ErkJggg==)
②のとき( )
)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{-1}\left(-t-1\right)dt+\frac{1}{2}\int_{-1}^{x+1}\left(t+1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2-t\right]_{x-1}^{-1}+\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{-1}^{x+1}=\frac{1}{2}\left(x^2+2x+2\right)](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAAA6AQAAAADDj/MPAAAAAnRSTlMAAHaTzTgAAAAbSURBVFjD7cEBDQAAAMKg909tDjegAAAAAPg3EeYAAXM2cu4AAAAASUVORK5CYII=)
③のとき( )
)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{-1}\left(-t-1\right)dt+\frac{1}{2}\int_{-1}^{0}\left(t+1\right)dt+\frac{1}{2}\int_{0}^{x+1}\left(-t+1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2-t\right]_{x-1}^{-1}+\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{-1}^0+\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_0^{x+1}=\frac{1}{2}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAAA4AQAAAACOR1IEAAAAAnRSTlMAAHaTzTgAAAAbSURBVFjD7cGBAAAAAMOg+VNf4QBVAQAAAPAYEUgAAYy9eIMAAAAASUVORK5CYII=)
④のとき( )
)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{-1}^{0}\left(t+1\right)dt+\frac{1}{2}\int_{0}^{1}\left(-t+1\right)dt=\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{-1}^0+\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_0^1=\frac{1}{2}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAngAAAAcAQAAAADaFv/yAAAAAnRSTlMAAHaTzTgAAAAYSURBVBgZYxgFo2AUjIJRMApGwSgYYgAACMAAAcZbCHcAAAAASUVORK5CYII=)
⑤のとき( )
)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{0}\left(t+1\right)dt+\frac{1}{2}\int_{0}^{1}\left(-t+1\right)dt+\frac{1}{2}\int_{1}^{x+1}\left(t-1\right)dt=\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{x-1}^0+\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_0^1+\frac{1}{2}\left[\frac{1}{2}t^2-t\right]_1^{x+1}=\frac{1}{2}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAAA4AQAAAACOR1IEAAAAAnRSTlMAAHaTzTgAAAAbSURBVFjD7cGBAAAAAMOg+VNf4QBVAQAAAPAYEUgAAYy9eIMAAAAASUVORK5CYII=)
⑥のとき( )
)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{1}\left(-t+1\right)dt+\frac{1}{2}\int_{1}^{x+1}\left(t-1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_{x-1}^1+\frac{1}{2}\left[\frac{1}{2}t^2-t\right]_1^{x+1}=\frac{1}{2}\left(x^2-2x+2\right)](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAAA6AQAAAADDj/MPAAAAAnRSTlMAAHaTzTgAAAAbSURBVFjD7cEBDQAAAMKg909tDjegAAAAAPg3EeYAAXM2cu4AAAAASUVORK5CYII=)
⑦のとき( )
)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{x+1}\left(t-1\right)dt=\frac{1}{2}\left[\frac{1}{2}t^2-t\right]_{x-1}^{x+1}=x-1](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAZIAAAAcAQAAAABjNARLAAAAAnRSTlMAAHaTzTgAAAATSURBVBgZYxgFo2AUjIJRMCQAAAWwAAEyKZ7FAAAAAElFTkSuQmCC)
まとめると,

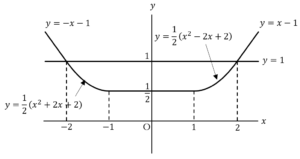
図示すると,

よって,求める面積は, 軸での対称性より,
軸での対称性より,
![Rendered by QuickLaTeX.com 2\left\{\frac{1}{2}\cdot1+\int_{1}^{2}\left\{1-\frac{1}{2}\left(x^2-2x+2\right)\right\}dx\right\}=1+2\left[-\frac{1}{6}x^3+\frac{1}{2}x^2\right]_1^2=\frac{5}{3}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAiYAAAAiAQAAAABDuy/UAAAAAnRSTlMAAHaTzTgAAAAZSURBVEjH7cExAQAAAMKg9U9tB2+gAAB4DQlMAAHOCrs0AAAAAElFTkSuQmCC) ……(答)
……(答)(2)
実数解が1と3であることから,他の二解を として,
として,

と書ける.係数比較すると,

となる.
次に,2次方程式 について考える.この方程式の解が1か3,或いは虚数解であれば,4次方程式
について考える.この方程式の解が1か3,或いは虚数解であれば,4次方程式 の実数解が1と3のみとなる.
の実数解が1と3のみとなる.
(Ⅰ) が実数のとき
が実数のとき
まず,判別式が非負となる必要があるので, が必要である.
が必要である.
このもとで,2次方程式 の解が1か3のみとなるには,
の解が1か3のみとなるには, なら必要十分(これらは全て
なら必要十分(これらは全て を満たす).この内,(*)式に抵触しないのは,
を満たす).この内,(*)式に抵触しないのは, のみである.このとき,(*)の第一式より,
のみである.このとき,(*)の第一式より, となる.
となる.
(Ⅱ) が虚数のとき
が虚数のとき
まず,判別式が負となる必要があるので, が必要である.
が必要である.
 が虚数ならば,
が虚数ならば, の値によらず,2次方程式
の値によらず,2次方程式 の解は虚数となる.
の解は虚数となる.
(*)を利用すれば,
以上(Ⅰ)と(Ⅱ)より,4次方程式 の実数解が1と3のみとなる
の実数解が1と3のみとなる の範囲は
の範囲は である.
である.
 は整数なので,求める最大値は
は整数なので,求める最大値は ,最小値は
,最小値は である.……(答)
である.……(答)(3)
 より,三角形
より,三角形 は
は の直角三角形である.
の直角三角形である.

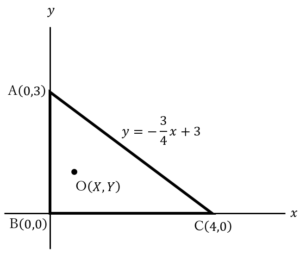
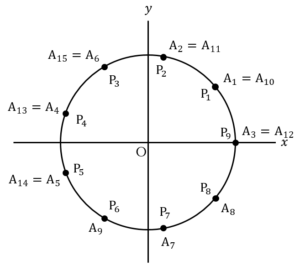
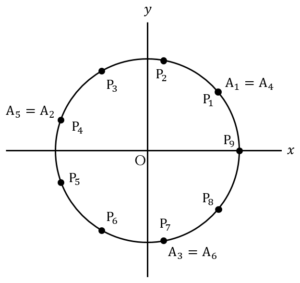
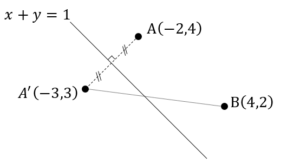
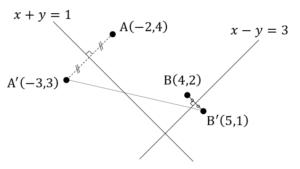
そこで,点 を原点として,左図のように三角形
を原点として,左図のように三角形 を
を 平面上にのせる.
平面上にのせる.
内部の点 の座標を左図のように
の座標を左図のように とおく.点
とおく.点 は三角形
は三角形 の内部の点であるので,
の内部の点であるので,
 ……(*)
……(*)
を満たす必要がある.
このもとで,

である.更に点と直線の距離の公式より,

である.

よって,
 で
で は最小となる.なお,
は最小となる.なお, は(*)を満たす.
は(*)を満たす.
このとき,
 ……(答)
……(答)(4)
 を固定して,
を固定して, となる
となる について考えると,
について考えると, より,
より,
 は
は について単調増加であり,
について単調増加であり, は単調減少であるから,
は単調減少であるから, の最小値は,
の最小値は, 以上である.
以上である.
よって, を満たすには,
を満たすには,

であれば十分.
 と
と が整数であることから,
が整数であることから,
 であれば十分.
であれば十分.
ここで, のときを考える.
のときを考える.
 であり
であり より,
より, の最小値は,
の最小値は, か
か である.
である.


より, であるから,
であるから, のとき条件(*)は満たされない.
のとき条件(*)は満たされない.
よって求める の最大値は63……(答)
の最大値は63……(答)






![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{-1}\left(-t-1\right)dt+\frac{1}{2}\int_{-1}^{x+1}\left(t+1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2-t\right]_{x-1}^{-1}+\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{-1}^{x+1}=\frac{1}{2}\left(x^2+2x+2\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-39f866a3cf0aa6d994ba926375844cd8_l3.png)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{-1}\left(-t-1\right)dt+\frac{1}{2}\int_{-1}^{0}\left(t+1\right)dt+\frac{1}{2}\int_{0}^{x+1}\left(-t+1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2-t\right]_{x-1}^{-1}+\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{-1}^0+\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_0^{x+1}=\frac{1}{2}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-6432dfc95b1fd3fc8ab0566581f9478a_l3.png)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{0}\left(t+1\right)dt+\frac{1}{2}\int_{0}^{1}\left(-t+1\right)dt+\frac{1}{2}\int_{1}^{x+1}\left(t-1\right)dt=\frac{1}{2}\left[\frac{1}{2}t^2+t\right]_{x-1}^0+\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_0^1+\frac{1}{2}\left[\frac{1}{2}t^2-t\right]_1^{x+1}=\frac{1}{2}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-b5cfbd01a7849bbc24254319f21aa456_l3.png)
![Rendered by QuickLaTeX.com f\left(x\right)=\frac{1}{2}\int_{x-1}^{1}\left(-t+1\right)dt+\frac{1}{2}\int_{1}^{x+1}\left(t-1\right)dt=\frac{1}{2}\left[-\frac{1}{2}t^2+t\right]_{x-1}^1+\frac{1}{2}\left[\frac{1}{2}t^2-t\right]_1^{x+1}=\frac{1}{2}\left(x^2-2x+2\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-02980b127b2365339e8eef20ba5c599a_l3.png)
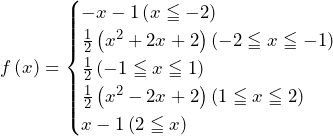
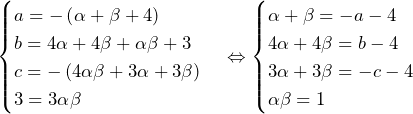
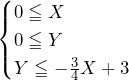 ……(*)
……(*)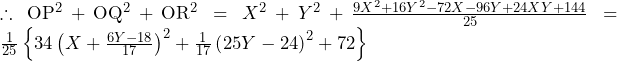
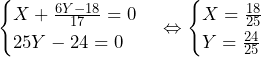 で
で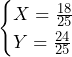 は(*)を満たす.
は(*)を満たす.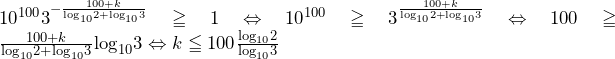
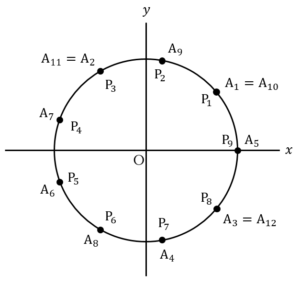

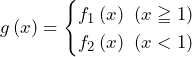
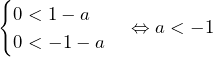 のとき
のとき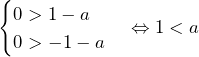 のとき
のとき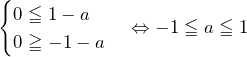 のとき
のとき
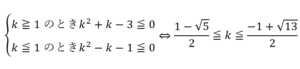
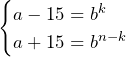
![Rendered by QuickLaTeX.com \int_{0}^{x}\left\{P\left(t\right)\right\}^mdt=\int_{0}^{x}\left\{at+b\right\}^2dt=\left[\frac{1}{3}a^2t^3+abt^2+b^2t\right]_0^x=\frac{1}{3}a^2x^3+abx^2+b^2x P\left(x^3\right)-P\left(0\right)=\left(ax^3+b\right)-b=ax^3](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a11b033768caae58621300cc339f8d26_l3.png)
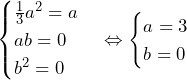
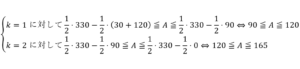
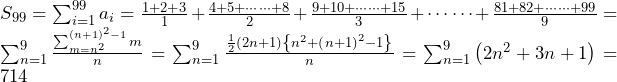 ……(答)
……(答)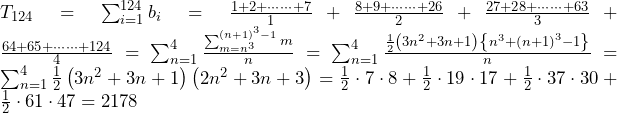 ……(答)
……(答)

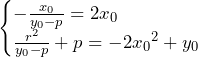
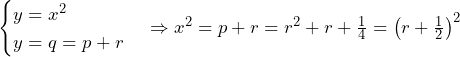
![Rendered by QuickLaTeX.com \int_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}\left(q-x^2\right)dx=\int_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}\left\{\left(r+\frac{1}{2}\right)^2-x^2\right\}dx=\left[\left(r+\frac{1}{2}\right)^2x-\frac{1}{3}x^3\right]_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}=\frac{4}{3}r^3+2r^2+r+\frac{1}{6}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-94aeca5089102bd3c6cc95fc6a86c7e9_l3.png) ……(答)
……(答)