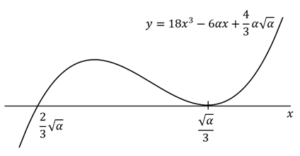
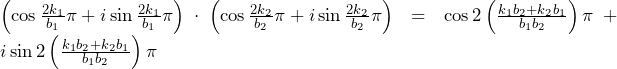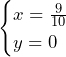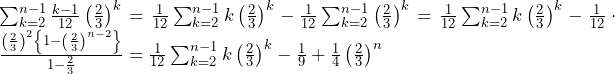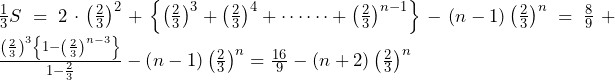早稲田大学理工過去問徹底研究 2018年 大問4 方針の立て方 (1) 素直に微分すればよい. (2) (ⅰ)通常の極値問題と同様に微分して考えればよい. (ⅱ)これも典型的な回転体の体積の問題であるため特筆事項なし. (ⅲ)実際にをはじめの数項を書き出してみれば,数列の和の問題だと分かる. 解答例
- …続きを読む
-
早稲田大学理工過去問徹底研究 2018年 大問4
方針の立て方
(1)
素直に微分すればよい.(2)
(ⅰ)通常の極値問題と同様に微分して考えればよい.
(ⅱ)これも典型的な回転体の体積の問題であるため特筆事項なし.
(ⅲ)実際に をはじめの数項を書き出してみれば,数列の和の問題だと分かる.
をはじめの数項を書き出してみれば,数列の和の問題だと分かる.解答例
(1)
積の微分法則を使えば,
 ……(答)
……(答)(2)
(ⅰ)
積の微分法則と三角関数の合成を用いれば,

よって, となるのは,
となるのは, (
( は任意の整数)のとき.
は任意の整数)のとき.
 が偶数のとき,その前後で
が偶数のとき,その前後で の符号は負から正となる.故に極小値は,
の符号は負から正となる.故に極小値は,
 が奇数のとき,その前後で
が奇数のとき,その前後で の符号は正から負となる.故に極大値は,
の符号は正から負となる.故に極大値は,
よって, を任意の整数として,
を任意の整数として,
極大値は ……(答)
……(答)
極小値は ……(答)
……(答)
(ⅱ)

ここで,
![Rendered by QuickLaTeX.com \int_{n-1}^{n}{\frac{1}{2}\pi e^{-2\pi x}}dx=\left[-\frac{1}{4}e^{-2\pi x}\right]_{n-1}^n=-\frac{1}{4}e^{-2n\pi}+\frac{1}{4}e^{-2\left(n-1\right)\pi}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAdsAAAAZAQAAAABRVrmSAAAAAnRSTlMAAHaTzTgAAAATSURBVBgZYxgFo2AUjIJRMHIAAAX1AAEEfQ1jAAAAAElFTkSuQmCC)
更に として置換積分を行えば,
として置換積分を行えば,
![Rendered by QuickLaTeX.com \int_{n-1}^{n}{\pi e^{-2\pi x}\cos{\left(-2\pi x\right)}}dx=-\frac{1}{2}\int_{-2\left(n-1\right)\pi}^{-2n\pi}{e^y\cos{y}}dy\bigm=-\frac{1}{2}\left[\frac{1}{2}e^y\left(\cos{y}+\sin{y}\right)\right]_{-2\left(n-1\right)\pi}^{-2n\pi}\bigm=-\frac{1}{4}\left(e^{-2n\pi}-e^{-2\left(n-1\right)\pi}\right)](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmMAAAA+AQAAAABPPCHQAAAAAnRSTlMAAHaTzTgAAAAbSURBVBgZ7cEBDQAAAMIg+6d+DjdgAAAAAHAuEuQAAUZ9B4oAAAAASUVORK5CYII=)
である.
 ……(答)
……(答)
(ⅲ)
 ……(答)
……(答)
(※無限等比級数の第2項と第3項,第4項と第5項,第6項と第7項,……が相殺される)
(別解)
 は,初項
は,初項 ,公比
,公比 の等比数列 (なお,
の等比数列 (なお, である).
である).
 ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。






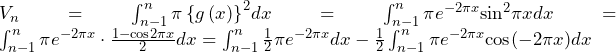
![Rendered by QuickLaTeX.com \int_{n-1}^{n}{\pi e^{-2\pi x}\cos{\left(-2\pi x\right)}}dx=-\frac{1}{2}\int_{-2\left(n-1\right)\pi}^{-2n\pi}{e^y\cos{y}}dy\bigm=-\frac{1}{2}\left[\frac{1}{2}e^y\left(\cos{y}+\sin{y}\right)\right]_{-2\left(n-1\right)\pi}^{-2n\pi}\bigm=-\frac{1}{4}\left(e^{-2n\pi}-e^{-2\left(n-1\right)\pi}\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-df13329429bcde4e2ecc7f39a38e588b_l3.png)
 ……(答)
……(答)
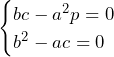
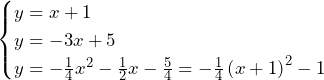
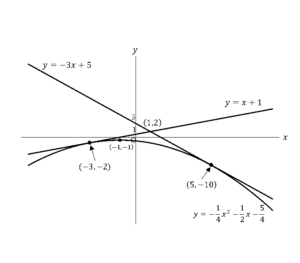
![Rendered by QuickLaTeX.com \int_{-3}^{1}\left\{\left(x+1\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx+\int_{1}^{5}\left\{\left(-3x+5\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx\bigm=\left[\frac{1}{12}x^3+\frac{3}{4}x^2+\frac{9}{4}x\right]_{-3}^1+\left[\frac{1}{12}x^3-\frac{5}{4}x^2+\frac{25}{4}x\right]_1^5=\frac{32}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-bbec6b7afbfd51917ee8a7761b2bc8b3_l3.png) ……(答)
……(答)


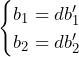 (
(