方針の立て方 (1)(3)(4)は基本問題であり,特筆事項なし.(4)は本解ではと丁寧に記述したが,であることと,解答形式は穴埋め形式である(途中の計算を記述しない)ため,本番では直ちに11と答えても良いだろう. (2)は少々考えにくい問題であるが,相関係数とは,1つのデータで決まるものではなく,他
- …続きを読む
-
方針の立て方
(1)(3)(4)は基本問題であり,特筆事項なし.(4)は本解では
 と丁寧に記述したが,
と丁寧に記述したが, であることと,解答形式は穴埋め形式である(途中の計算を記述しない)ため,本番では直ちに11と答えても良いだろう.
であることと,解答形式は穴埋め形式である(途中の計算を記述しない)ため,本番では直ちに11と答えても良いだろう.
(2)は少々考えにくい問題であるが,相関係数とは,1つのデータで決まるものではなく,他のデータとの関係で決まるものであるから,複数のデータを比較することが必要だと考える.
相関係数0.95以上というのは大変強い正の相関であり,殆ど比例の関係だと見做せる.解答例
(34)(35)52
(36)(37)74
(38)0
(39)1
(40)3
(41)5
(42)6
(43)(44)(45)68.2
(46)(47)(48)68.4
(49)9
(50)(51)11解説
(1)
表より,最小値は52,最大値は74……(答)(2)
番号2の個体と比較して,「体長が大きく,体重も大きい」か「体長が小さく,体重も小さい」のどちらかに該当する番号の個体は種類Bに分類される可能性があり,該当する番号は(2を除いて)4,5,6,7,8,9である.
逆にこれに該当しない番号0,1,3の個体は種類Aに分類される.
番号0の個体と比較して,「体長が大きく,体重も大きい」か「体長が小さく,体重も小さい」のどちらかに該当する番号の個体は種類Aに分類される可能性があり,該当する番号は(0,1,3を除いて)5,6である.よって,種類Aの5匹の番号は小さい方から0,1,3,5,6……(答)
また,種類Aの5匹の体長の平均値は, ……(答)
……(答)(3)
10匹のうち体長の大きい方から5匹の個体の番号は1,3,5,6,9であり,この5匹の体長の平均値は, ……(答)
……(答)
種類Bの5匹の番号は2,4,7,8,9であるから,体長の大きい5匹のうち種類Bの個体の番号は9……(答)(4)
 ……(答)
……(答)







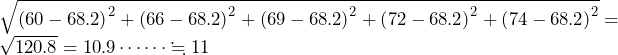 ……(答)
……(答)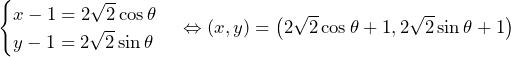 とおくことができる(
とおくことができる(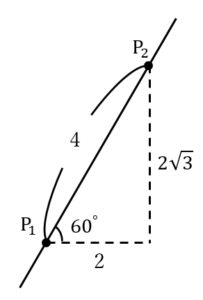
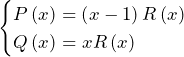 ……(*)
……(*)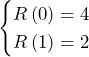
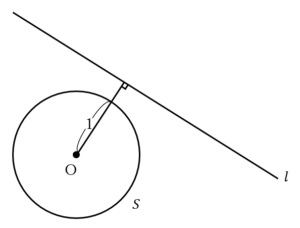
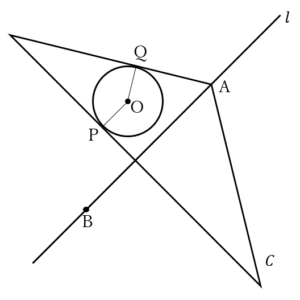
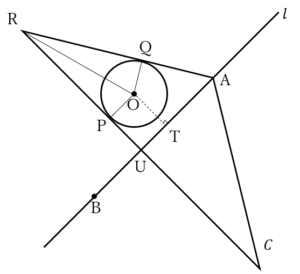

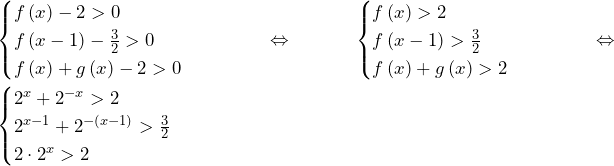
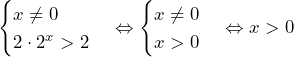
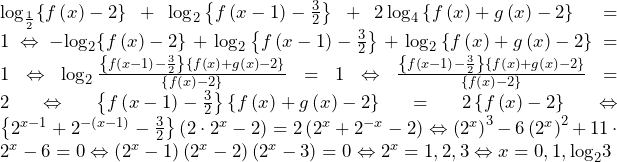
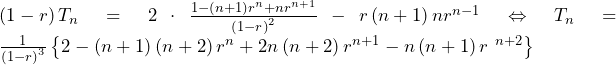 ……(答)
……(答)![Rendered by QuickLaTeX.com \int_{0}^{2}\left(-6x+15\right)dx=\left[-3x^2+15x\right]_0^2=18,\int_{0}^{2}\left(-3x^2+12\right)dx=\left[-x^3+12x\right]_0^2=16](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-c3bfa33edb30774157f6fafbfffed269_l3.png)
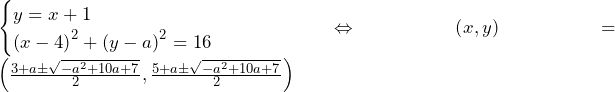 (複号同順)
(複号同順)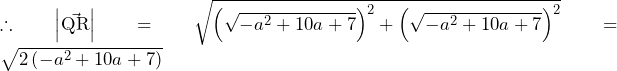
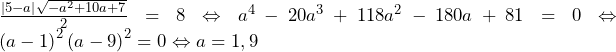 ……(答)
……(答)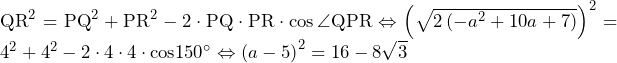 ……(答)
……(答)