方針の立て方 (1) 絶対値の問題では,絶対値の中身の正負で場合分けをする.すると,を境目にして場合分けが生じることが分かるため,本解答の(ⅰ)~(ⅲ)のように場合分けすることが分かる. (2) 考える図形を図示して,どこの面積を求めれば良いかを特定する.後は積分計算を行うだけ. (3) 解析を行う
- …続きを読む
-
方針の立て方
(1)
絶対値の問題では,絶対値の中身の正負で場合分けをする.すると, を境目にして場合分けが生じることが分かるため,本解答の(ⅰ)~(ⅲ)のように場合分けすることが分かる.
を境目にして場合分けが生じることが分かるため,本解答の(ⅰ)~(ⅲ)のように場合分けすることが分かる.(2)
考える図形を図示して,どこの面積を求めれば良いかを特定する.後は積分計算を行うだけ.(3)
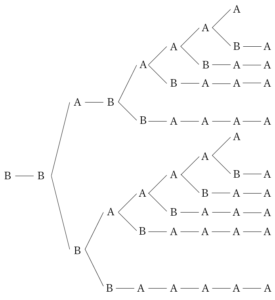
解析を行うには,点 の座標を具体的に書き下す必要があるが,そのままでは全部で(点
の座標を具体的に書き下す必要があるが,そのままでは全部で(点 がどの関数上に乗っているかで)6通りを考えることになる.高々6通りであるから,このまま考えても良いが,もう少し絞れないかを検討してみる.実際に満たす点
がどの関数上に乗っているかで)6通りを考えることになる.高々6通りであるから,このまま考えても良いが,もう少し絞れないかを検討してみる.実際に満たす点 を具体的に考えると,点
を具体的に考えると,点 は
は 軸の左側,点
軸の左側,点 は
は 軸の右側になければならないと分かるから,点
軸の右側になければならないと分かるから,点 は必ず
は必ず 上に乗っていると分かる.これより,考えるべきパターンは2通りに減少する.後は,本解答のように解析するのみ.
上に乗っていると分かる.これより,考えるべきパターンは2通りに減少する.後は,本解答のように解析するのみ.解答例
(1)
 となる.
となる.
(ⅰ) のとき
のとき
![Rendered by QuickLaTeX.com F\left(x\right)=-x-1+\int_{-1}^{x}\left(1+t\right)dt=-x-1+\left[t+\frac{1}{2}t^2\right]_{-1}^x=\frac{1}{2}x^2-\frac{1}{2}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAhsAAAAYAQAAAAB7VwKXAAAAAnRSTlMAAHaTzTgAAAAUSURBVBgZYxgFo2AUjIJRMAroCAAGeAABzdlMXAAAAABJRU5ErkJggg==)
(ⅱ) のとき
のとき
![Rendered by QuickLaTeX.com F\left(x\right)=x+1+\int_{-1}^{x}\left(1+t\right)dt=x+1+\left[t+\frac{1}{2}t^2\right]_{-1}^x=\frac{1}{2}x^2+2x+\frac{3}{2}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAikAAAAYAQAAAAAXUVCSAAAAAnRSTlMAAHaTzTgAAAAVSURBVBgZYxgFo2AUjIJRMAoGMQAABqgAAaZk08wAAAAASUVORK5CYII=)
(ⅲ) のとき
のとき
![Rendered by QuickLaTeX.com F\left(x\right)=x+1+\int_{-1}^{0}\left(1+t\right)dt+\int_{0}^{x}\left(1-t\right)dt=x+1+\left[t+\frac{1}{2}t^2\right]_{-1}^0+\left[t-\frac{1}{2}t^2\right]_0^x=-\frac{1}{2}x^2+2x+\frac{3}{2}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmkAAAA2AQAAAAC0TTN0AAAAAnRSTlMAAHaTzTgAAAAbSURBVFjD7cExAQAAAMKg9U9tDQ+gAAAAAF4MEKoAAWWELMgAAAAASUVORK5CYII=)
以上,(ⅰ)~(ⅲ)より,
 ……(答)
……(答)(2)
前問で求めた のグラフを描くと,
のグラフを描くと,

上図.
よって,求める面積は,
![Rendered by QuickLaTeX.com \int_{-1}^{0}\left(\frac{1}{2}x^2+2x+\frac{3}{2}\right)dx+\int_{0}^{2+\sqrt7}\left(-\frac{1}{2}x^2+2x+\frac{3}{2}\right)dx=\left[\frac{1}{6}x^3+x^2+\frac{3}{2}x\right]_{-1}^0+\left[-\frac{1}{6}x^3+x^2+\frac{3}{2}x\right]_0^{2+\sqrt7}=\frac{19+7\sqrt7}{3}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmgAAAA/AQAAAAB8gAmCAAAAAnRSTlMAAHaTzTgAAAAbSURBVFjD7cExAQAAAMKg9U/taQmgAAAAAIAbEzIAAdzBpmkAAAAASUVORK5CYII=) ……(答)
……(答)(3)
 かつ
かつ が必要であり,
が必要であり, となる.
となる.
(ⅰ) のとき
のとき
 となる.
となる.
よって, を結ぶ線分の中点の座標は,
を結ぶ線分の中点の座標は, と書ける.これが
と書ける.これが であるとき,
であるとき,

これは かつ
かつ を満たす.よって,
を満たす.よって, となる.
となる.
このとき傾き は,
は, となる.
となる.
(ⅱ) のとき
のとき
 となる.
となる.
よって, を結ぶ線分の中点の座標は,
を結ぶ線分の中点の座標は, と書ける.これが
と書ける.これが であるとき,
であるとき,

 より,
より, .これは
.これは を満たす.よって,
を満たす.よって, となる.
となる.
このとき傾き は,
は, となる.
となる.
 より,
より,
以上,(ⅰ)と(ⅱ)より,求める範囲は,
 ……(答)
……(答)







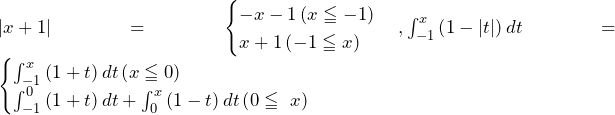 となる.
となる.![Rendered by QuickLaTeX.com F\left(x\right)=x+1+\int_{-1}^{0}\left(1+t\right)dt+\int_{0}^{x}\left(1-t\right)dt=x+1+\left[t+\frac{1}{2}t^2\right]_{-1}^0+\left[t-\frac{1}{2}t^2\right]_0^x=-\frac{1}{2}x^2+2x+\frac{3}{2}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-41c71a6f673b63fa745fc3d548c4ed52_l3.png)
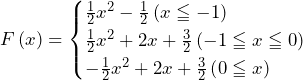 ……(答)
……(答)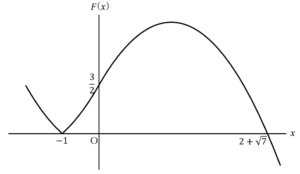
![Rendered by QuickLaTeX.com \int_{-1}^{0}\left(\frac{1}{2}x^2+2x+\frac{3}{2}\right)dx+\int_{0}^{2+\sqrt7}\left(-\frac{1}{2}x^2+2x+\frac{3}{2}\right)dx=\left[\frac{1}{6}x^3+x^2+\frac{3}{2}x\right]_{-1}^0+\left[-\frac{1}{6}x^3+x^2+\frac{3}{2}x\right]_0^{2+\sqrt7}=\frac{19+7\sqrt7}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-49c0c64db15f48db2771431bf99b4c3e_l3.png) ……(答)
……(答)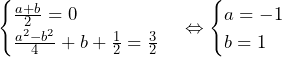
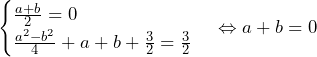
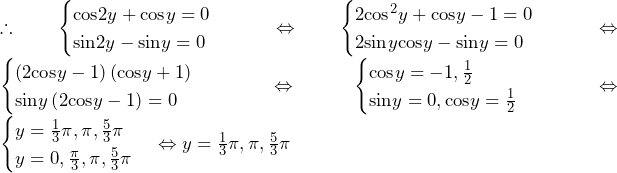 ……(答)
……(答)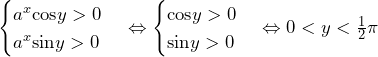
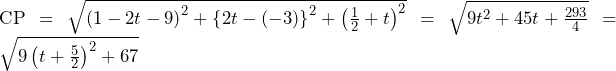
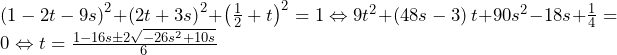
 ……(答)
……(答)
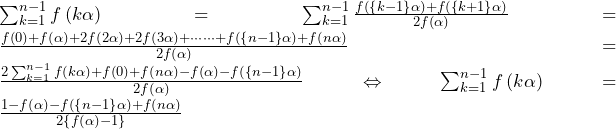
![Rendered by QuickLaTeX.com A=\int_{0}^{2}f\left(t\right)dt=\int_{0}^{2}\left(\frac{3}{a}t^2-\frac{1}{a}t+A^2\right)dt=\left[\frac{1}{a}t^3-\frac{1}{2a}t^2+A^2t\right]_0^2=2A^2+\frac{6}{a}\Leftrightarrow2A^2-A+\frac{6}{a}=0](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-ab0bf548b4a46975e7979ac67d04290f_l3.png)
![Rendered by QuickLaTeX.com \int_{0}^{b}\left\{f\left(x\right)-f\left(b\right)\right\}dx=\int_{0}^{b}\left\{\frac{3}{a}x^2-\frac{1}{a}x-\frac{3}{a}b^2+\frac{1}{a}b\right\}dx=\left[\frac{1}{a}x^3-\frac{1}{2a}x^2-\frac{3}{a}b^2x+\frac{1}{a}bx\right]_0^b=-\frac{b^2\left(4b-1\right)}{2a}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a1ae218f005a4a94ff3accbf2e2f76ee_l3.png)
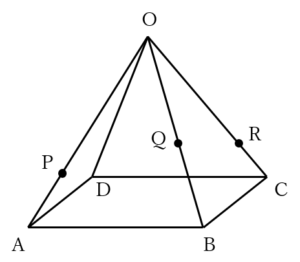
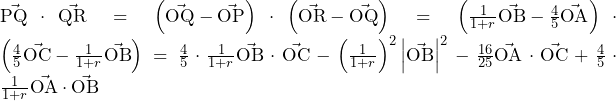
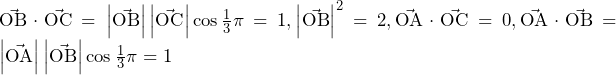 であるから,
であるから,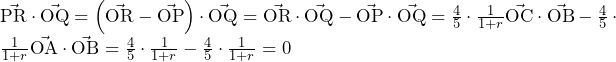 ……(答)
……(答)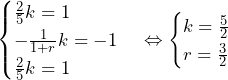
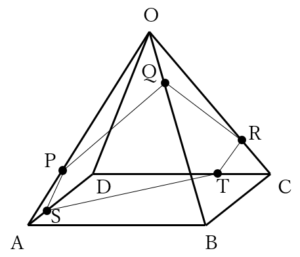
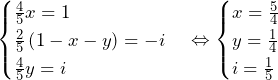
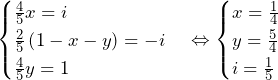
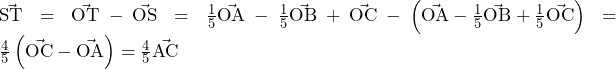
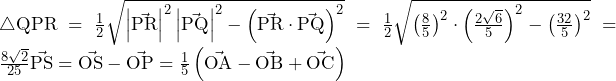 より,
より,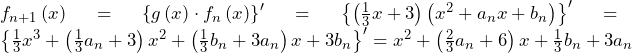
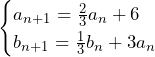 ……(答)
……(答)
 ……(答)
……(答)
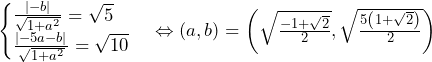
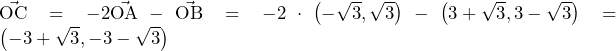
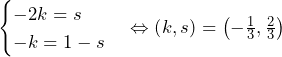
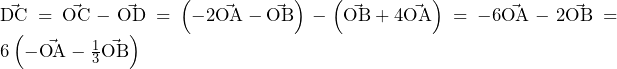
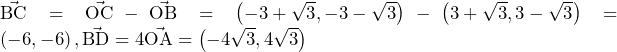 より,
より,