ページ目次青山学院大学文学部英語の対策/勉強法青山学院大学文学部英語の全体総括青山学院大学文学部に合格するための参考書青山学院大学文学部に圧倒的な実力で合格できる専門対策をします 青山学院大学文学部英語の対策/勉強法 渋谷の青山にキャンパスがあることもあり、人気が急上昇の青山学院大学です。青山や立教
- …続きを読む
-
青山学院大学文学部英語の対策/勉強法
渋谷の青山にキャンパスがあることもあり、人気が急上昇の青山学院大学です。青山や立教はその場所やキャンパスから女の子に人気が高く、その中でも一般的に文学部は女性が多いため、偏差値が高くなっています。
[word_balloon id="1" balloon="line" name_position="under_avatar" name="ブタトン" radius="true" avatar_border="false" avatar_shadow="false" balloon_shadow="false" avatar_hide="false" box_center="false" font_size="17" name_color="#10193a" position="R" bg_color="#8de055" font_color="#fff"]大人気の青学の看板学部です![/word_balloon]青山学院は一般的にMARCHの中でも英語が難し目ですが、文学部は中でも特に英語の難易度が高くなっています。配点も英語が2倍(英語200,その他100点)と高くなっています。
志望する学科によって問題が異なるのですが、英文科を目指す生徒はリスニングの試験もあるので、対策を怠らないように注意して下さい。本記事では青山学院大学文学部の英語について解説いたします。他の科目については下記よりご確認ください。
[su_box title="青山学院大学文学部 科目別対策" radius="1"]▶英語対策 ▶国語対策 ▶日本史対策 ▶世界史対策 [/su_box] [toc]青山学院大学文学部英語の全体総括
全体概観:配点200点 時間100分
長文、和訳、英訳、自由英作文、文法、リスニング(英米志望であれば)と様々な問題形式で出題されます。
[word_balloon id="1" balloon="line" name_position="under_avatar" name="ブタトン" radius="true" avatar_border="false" avatar_shadow="false" balloon_shadow="false" avatar_hide="false" box_center="false" font_size="17" name_color="#10193a" position="R" bg_color="#8de055" font_color="#fff"]リスニングは別の試験で代替している学校が多いのですが、青学文学部では今もリスニングをしています[/word_balloon]
そのため、通常の英文読解を行うだけでなく、全方位的な学習が望まれます。長文読解問題について
長文問題は例年2題出題されます。そのうち1題は800~1000字程度の長文となっています。
問題文は長いですが、問題を解くこと自体は難しくありません。
選択肢にある意味を取り違えたりなどの凡ミスをしないように基本的語彙、熟語の習得を怠らないようにしましょう。速読ができるようにするためには?
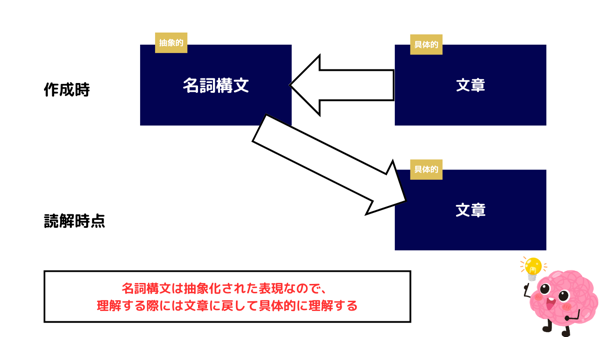
[word_balloon id="1" balloon="line" name_position="under_avatar" name="ブタトン" radius="true" avatar_border="false" avatar_shadow="false" balloon_shadow="false" avatar_hide="false" box_center="false" font_size="17" name_color="#10193a" position="R" bg_color="#8de055" font_color="#fff"]長文を解くために必要な速読力を身につけるために必要なのは、どのようなことが必要なのかみていきましょう![/word_balloon]英語を英語として理解できるようにするための構文把握力をつけることです。勉強を始めたときは英語を見た時に呪文のように感じて何をどのように読んでいったら良いのかわからないかもしれません。
ですが、英語長文を読みながら、SVOCといった構文を把握しながら英語を読んでいくことで英語を英語のカタマリとして読むことができて意味を理解することができるようになるのです。まずは基本レベルとして『句とは?』『節とは何か?』そして『そのカタマリがどのような品詞になるのか?』といったことを長文を読んだ瞬間に瞬時に把握できるようにしていきましょう。
昨今の入試は本入試と同じように長い文章をいかに速く処理して、内容を掴んでいくのか?というのが重要な部分になってきます。基礎の基礎として構文をどのように取ったら良いのかは、こちらの記事で説明しています。
[nlink url="https://hiroacademia.jpn.com/blog/program/saisokuenglishreading-svoc-structure/"]速解ができるようになるためには?
英語を英語として捉えることができたのであれば、速く解くことができるようになるのが大事です。入試では時間内に得点を取らないと点数にはなりません。速く読むことよりも、いかにして速く解くことができるのか?という点に重点をおいたほうがよいでしょう。
問題を速く解くためには、問題を読む際のメモのとり方、まとめ方が大いに得点に関わってきます。合格する人はこの部分が大きく異なっていますので、自身で勉強をする時には意識していきましょう。ただ読み流すだけでは、問題を速くことはできません。
[nlink url="https://hiroacademia.jpn.com/blog/program/saisokuenglishreading-solving-process/"]
速く解くためには速く解くための方法があります。当塾では英語を偏差値30から合格水準まで短期間で指導していきます。
日本語訳問題
日本語訳=下線部だけ読んで答える・・・と考えている人が多いかもしれません。確かに赤本などの答えを見ると、そのように見えるでしょう。
ですが、大学側としては文章内の文脈に沿った訳をしてもらうことを想定しています。
ただ英語を単語に置き換えただけの意味のわからない訳にならないように注意が必要です。*代名詞を訳す場合があるかどうかは、設問に従いましょう。基本は訳さないで問題ありませんが設問で指定される場合があるので注意して下さい。
英訳問題
英訳=知っている単語と文法を駆使してとりあえず並べてみると勉強をしている人にとってはかなり難しく感じるでしょう。知っている単語と文法というのは間違えないのですが、英訳をする際には表現の際のルールを覚える必要があります。
ある程度,自身で発信できるレベルの英語例文を暗記したら、過去問を解いていき英語ができる人から添削を受けましょう。英訳問題を乗り切るのにオススメの教材は『ドラゴンイングリッシュ』です。こちらに使い方を載せていますので、ご確認下さい。
[nlink url="http://hiroacademia.jpn.com/blog/sankosyo/eigo/dragonenglish/"]自由英作文
順番としては上記の英訳問題ができるようになった段階で、自由英作文に取り組みましょう。自由英作文のテーマ自体は、自転車に乗る時にヘルメットをつけるべきか?といった基本的なテーマの出題となっております。
そのため、自由英作文の準備さえしておけば難なく答えることができるでしょう。こちらで詳しい英作文の勉強法をお伝えしているのでご確認下さい。
[nlink url="http://hiroacademia.jpn.com/blog/program/writing-benkyo/"]リスニング
英米文学科のみに出題。読解と同じ程度の内容を耳で聞いていく必要があります。そのため、英語のニュースを聞いて単語しか聞き取れない・・・というレベルの学生では合格は難しいです。リスニングは読解と同じで長期間のトレーニングが必要な分野です。
[word_balloon id="1" balloon="line" name_position="under_avatar" name="ブタトン" radius="true" avatar_border="false" avatar_shadow="false" balloon_shadow="false" avatar_hide="false" box_center="false" font_size="17" name_color="#10193a" position="R" bg_color="#8de055" font_color="#fff"]リスニング=センスだと思っている人も多いですが正しい勉強に沿って行えばちゃんとできるようになりますよ![/word_balloon]こちらで詳しいリスニングの勉強法をお伝えしているのでご確認下さい。
[nlink url="http://hiroacademia.jpn.com/blog/program/listening-benkyo/"]青山学院大学文学部に合格するための参考書
当塾で使用している青山学院大学文学部に合格へ必要な参考書を紹介します。もちろん、当塾の場合は一人一人個別にカリキュラムを作成するため下記のようなカリキュラムは一例となります。参考書は何をやるかよりも、どのような目的で使用するかというが大事です。闇雲に行って情報量に圧倒されてしまうのではなく、1つ1つ目的意識を持って勉強していきましょう。
[nlink url="https://hiroacademia.jpn.com/blog/program/saisokuenglishreading-schedule/"]参考書だけでの独学での合格はかなり難しく、初学者の場合は指導なしでやってしまうと下手な癖が付く可能性が高いです。下手な癖がつくと、その癖を治すのに手一杯で結局志望校に受からないというケースが多くなっています。浪人しても成功しない人はこの辺りに理由があります。
ご心配な方は一度カウンセリングを受けて見ると良いでしょう。カウンセリングはこちらからどうぞ。青山学院大学文学部は1000字近くの長文に加えて、自由英作文が課されます。長文は1から丁寧に読んでいくのではなく、大事なところと大事でない部分を見分けて緩急のつけた読み方が必要になってきます。また自由英作文については、青山学院大学文学部に合格するための書き方がございます。
当塾では一人一人丁寧にこのレベルに到達することができるまで指導していきます。青山学院大学文学部に圧倒的な実力で合格できる専門対策をします
まずは資料請求・お問い合わせ・学習相談から!
HIRO ACADEMIAには、青山学院大学専門として文学部への圧倒的な合格ノウハウがございます。
少しでもご興味をお持ちいただいた方は、まずは合格に役立つノウハウや情報を、詰め込んだ資料をご請求ください。
また、青山学院大学文学部に合格するためにどのよう勉強をしたらよいのかを指示する学習カウンセリングも承っています。学習状況を伺った上で、残りの期間でどう受かるかを提案いたしますので、ぜひお気軽にお電話いただければと思います。









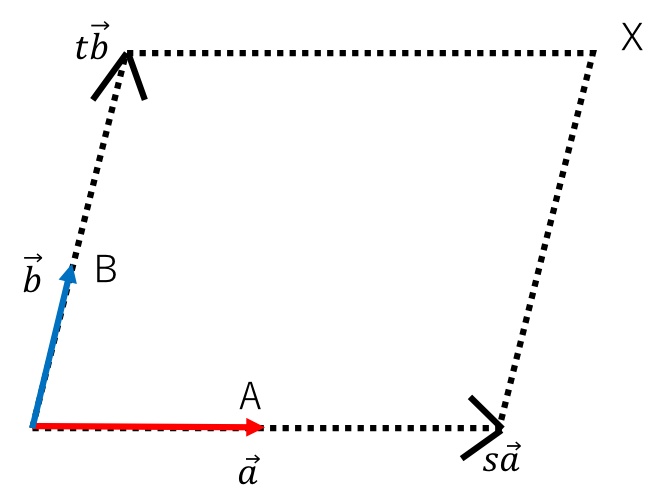
 図2
図2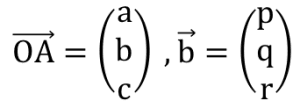


 なので、線分OA上にz=tを満たす点A’が存在する。
なので、線分OA上にz=tを満たす点A’が存在する。 と表せる。
と表せる。 図4
図4
 で線分OA上にz=tを満たす点が存在しなく、線分AB、AC、OCを共通にもつ。
で線分OA上にz=tを満たす点が存在しなく、線分AB、AC、OCを共通にもつ。 ・・・(タ)
・・・(タ)
 図6
図6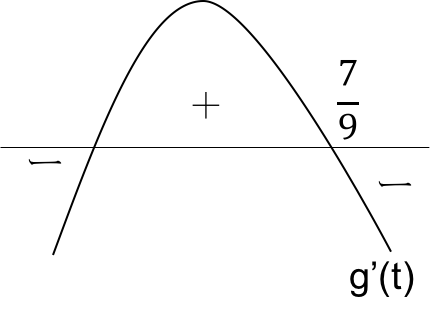 図7
図7
 とおける。(i)より
とおける。(i)より ・・・(ソ)
・・・(ソ)
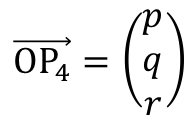 とおくと、
とおくと、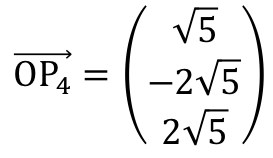 ・・・(タ)
・・・(タ)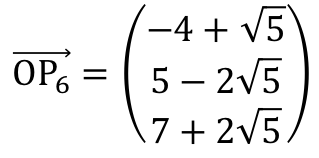 ・・・(チ)
・・・(チ)
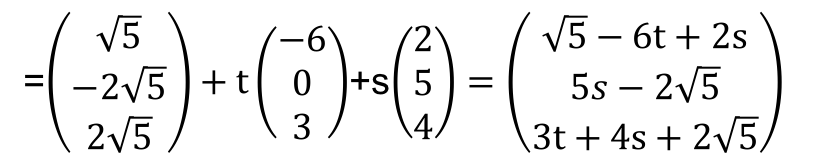












![Rendered by QuickLaTeX.com \therefore\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}<0\Leftrightarrow\left({\mathrm{log}}_2{t}\right)^2\left\{\left({\mathrm{log}}_2{t}\right)^2-4\right\}<0\Leftrightarrow \begin{cases} {\mathrm{log}}_2{t}\neq0 \\ \left({\mathrm{log}}_2{t}\right)^2-4<0 \end{cases}\Leftrightarrow\begin{cases} t\neq1 \\ \frac{1}{4}<t<4 \end{cases}\Leftrightarrow\frac{1}{4}<t<1,1<t<4](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-8e0527003541c856f39f9c25a8c98acf_l3.png)
![Rendered by QuickLaTeX.com \therefore\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}=0\Leftrightarrow\left({\mathrm{log}}_2{t}\right)^2\left\{\left({\mathrm{log}}_2{t}\right)^2-4\right\}=0\Leftrightarrow{\mathrm{log}}_2{t}=0,\left({\mathrm{log}}_2{t}\right)^2-4=0\Leftrightarrow t=\frac{1}{4},1,4](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a1e1073ddd84432fcb4f616a108cf763_l3.png)
![Rendered by QuickLaTeX.com x=\left({\mathrm{log}}_2{t}\right)^2+1\pm\sqrt{\left[-\left\{\left({\mathrm{log}}_2{t}\right)^2+1\right\}\right]^2-1\cdot\left\{6\left({\mathrm{log}}_2{t}\right)^2+1\right\}}=\left({\mathrm{log}}_2{t}\right)^2+1\pm\log_2{t}\sqrt{\left({\mathrm{log}}_2{t}\right)^2-4}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-200c81e8a0ef4ddb7ff42a6bac0604ed_l3.png)
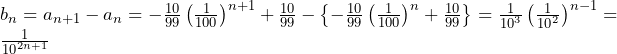
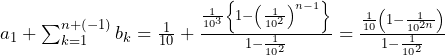
![Rendered by QuickLaTeX.com S_n=\sum_{k=1}^{n}\left\{\frac{1}{{10}^{2k}}\cdot{10}^{2k+1}\left(\frac{1}{a_k}-\frac{1}{a_{k+1}}\right)\right\}=10\sum_{k=1}^{n}\left(\frac{1}{a_k}-\frac{1}{a_{k+1}}\right)=10\left\{\left(\frac{1}{a_1}-\frac{1}{a_2}\right)+\left(\frac{1}{a_2}-\frac{1}{a_2}\right)+\cdots\cdots+\left(\frac{1}{a_n}-\frac{1}{a_{n+1}}\right)\right\}=10\left(\frac{1}{a_1}-\frac{1}{a_{n+1}}\right)=10\left[10-\frac{1-\frac{1}{{10}^2}}{\frac{1}{10}\left\{1-\frac{1}{{10}^{2\left(n+1\right)}}\right\}}\right]=\frac{1-\frac{1}{{10}^{2n}}}{1-\frac{1}{{10}^{2n+2}}}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a4bd52877826782c69edb6098ac4819d_l3.png)