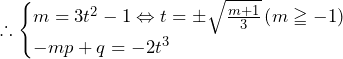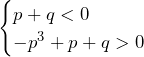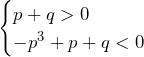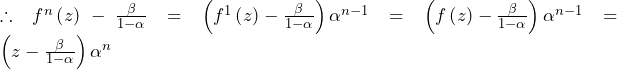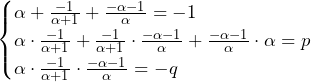2018年慶應義塾大学総合政策|過去問徹底研究 大問4 方針の立て方 (1) 解に関する情報が与えられているので,解を文字で置くという解法を取ろう. 問題文ではとが問われているため,解と係数の関係を用いて,とを引っ張り出すのが都合がいいと考えると方針を得られる.の未知数5つに対して,解と係数の関係で
- …続きを読む
-
2018年慶應義塾大学総合政策|過去問徹底研究 大問4
方針の立て方
(1)
解に関する情報が与えられているので,解を文字で置くという解法を取ろう.
問題文では と
と が問われているため,解と係数の関係を用いて,
が問われているため,解と係数の関係を用いて, と
と を引っ張り出すのが都合がいいと考えると方針を得られる.
を引っ張り出すのが都合がいいと考えると方針を得られる. の未知数5つに対して,解と係数の関係で得られる方程式は5つあるため,この方程式を解きさえすれば答えが得られると判断し,後はひたすらに計算をする.
の未知数5つに対して,解と係数の関係で得られる方程式は5つあるため,この方程式を解きさえすれば答えが得られると判断し,後はひたすらに計算をする.(2)
未知数が の一文字だけなので,一先ずは3次方程式をなんとか解けないかと考える.すると,2次方程式の問題に帰着させられる.
の一文字だけなので,一先ずは3次方程式をなんとか解けないかと考える.すると,2次方程式の問題に帰着させられる.
2次方程式に帰着させた後は,問題文で解のことが問われていることから,解の公式を使って,強引に解を表現することを試みる.後は必要条件で答えの候補を炙り出し,個々について十分性を検証することで,真の答えを絞り込んでいく.解答例
(31)(32)(33)(34)……
(35)(36)(37)(38)……
(39)(40)……
(41)(42)(43)(44)……
解説
(1)
共通解を として,3次方程式のもう一つの解を
として,3次方程式のもう一つの解を とする.解と係数の関係から,
とする.解と係数の関係から,


これを解くと,
 ……(答)
……(答)(2)

 の解は,
の解は,

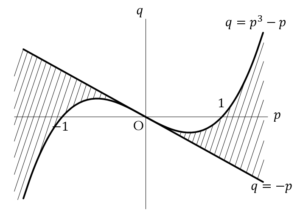
よって,題意を満たすには, (
( は4以上の自然数)が必要.
は4以上の自然数)が必要.

 はともに整数で,
はともに整数で, であるから,上式を満たす可能性があるのは,
であるから,上式を満たす可能性があるのは,

の4つである.これらを解くと,順番に,

 はともに整数であるから,適当なのは,
はともに整数であるから,適当なのは, のみ.これより,答えは,
のみ.これより,答えは, のときで,整数ではない有理数解は
のときで,整数ではない有理数解は ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。







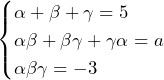
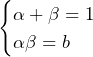
 ……(答)
……(答)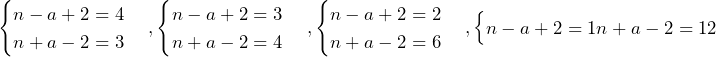
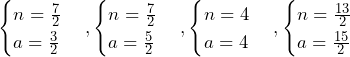
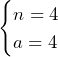 のみ.これより,答えは,
のみ.これより,答えは,
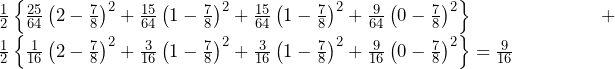 ……(答)
……(答)


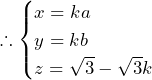
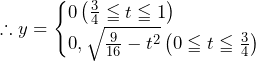 で
で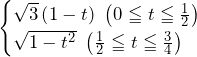
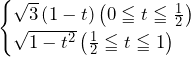
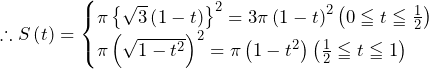 ……(答)
……(答)![Rendered by QuickLaTeX.com V=\int_{0}^{1}S\left(t\right)dt=\int_{0}^{\frac{1}{2}}{3\pi\left(1-t\right)^2}dt+\int_{\frac{1}{2}}^{1}\pi\left(1-t^2\right)dt=\left[-\pi\left(1-t\right)^3\right]_0^{\frac{1}{2}}+\left[\pi\left(t-\frac{1}{3}t^3\right)\right]_{\frac{1}{2}}^1=\frac{13}{12}\pi](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-23dadfd7a2f6b605eb35cb7bc70d9990_l3.png) ……(答)
……(答)