慶應義塾大学理工学部
理工学部の物理は空所補充問題が主に出題されます。一問あたりにかけられる時間が非常に短いため、問題そのものに対する思考力ももちろんですが、解ける問題を迅速に判断して解答していくための判断力が必要となります。
全体概観:配点100点 時間120分(理科2科目合計)
例年大問は3題で、空所補充形式となっています。ただし、一部選択問題や描図問題も出題されます。物理の配点は基本的には100点です。
理科は1科目あたり60分と時間が限られているので、解ける問題を見きわめて素早く解くことが大切になります。難しいと思ったら考えこまずに、一旦別の問題に移ることも大事です。
また、マークシートの問題の場合、数多く解くにつれて単位などで明らかにおかしいと感じる選択肢がわかるようになることがあります。
そのため、演習をするにつれ解くスピードが上がることが考えられます。
出題分野・形式
力学と電磁気から毎年大問1問ずつ出題されています。
残りの1問は、波動と熱力学のどちらかから大問1問が出題されています。
○各分野について
・力学:単振動、運動量保存則、力学的エネルギー保存則などがよく出題されます。思考力が問われる問題が多いのが特徴です。
・電磁気:電磁誘導、コンデンサー、ローレンツ力などがよく出題されます。また複合問題が出題されるのが特徴です。
・波動:よく出る分野というのはあまりなく、幅広く出題されます。ドップラー効果や光の干渉など基本的事項の応用が出題されることが多いのが特徴です。
・熱力学:気体の状態変化、ボイルシャルルの法則、熱力学第一法則などがよく出題されます。またサイクルの問題や熱効率を出させる問題も出題されます。

- 【何からはじめたらいい?という人向け】
【まず始めることをお伝えします】 - 早慶に合格するための戦略とは?
1,2年生から合格するための戦略を立てるには? - 【高1】早慶現役合格の勉強法を徹底解説
志望校に合格するためにやるべきこと紹介 - 【高2】現役で早慶GMARCHに合格
必要な勉強法(勉強時間、参考書)を紹介 - 【高2】早慶絶対合格!!のためにすること
勉強時間、スケジュール、参考書、勉強法の紹介
対策
基本事項の確認、問題演習
単なる公式の暗記だけでは通用しない問題がほとんどです。教科書に載っている基本法則の意味や物理量の定義を正しく理解しておくことが大切です。そのために基本的な物理の公式の導出も理解しておくことが重用です。グラフの問題も、法則の意味を理解していれば簡単に答えを出せることがほとんどなので、現象の様子と数式を対応付けて理解することが求められます。
図を描いて理解する

- 早慶は浪人しても難しい!?
根本的に変えていく必要性とその方法を伝授 - 【早慶浪人】伸びないのはなぜ?
伸ばし方を説明 - ヒロアカの浪人生必勝必勝コース
基礎から合格するための勉強法 - 【早慶浪人】年間スケジュール
浪人生が早慶に合格するための計画の立て方とは - 【早慶】女子浪人が絶対に合格には
志望校に合格するためにやるべきこと紹介 - 【早慶】3月にやっておくこと
早慶を目指す浪人生が絶対に3月にやっておくことを紹介
慶應レベルの問題になると、問題状況をまず正しく判断することが求められます。そのためにも、問題に対処するためには、簡単な問題でも図を描いて理解することが重要です。力学の「どこを起点にどの力が働いているか」や、波動のドップラー効果などは、図を描くことでイメージしやすくなります。状況が複雑になるほど図を描くことが必須になっていくので、早いうちから図を書いて理解することが大事です。
早く正確に計算できる力をつける
理科が2科目で1科目あたりにかけられる時間は60分ですが、その時間に対して問題量が非常に多いため、計算力が求められます。日頃の問題演習で、計算過程を書きながら問題を解くことが大事です。また、物理では単なる数学とは違い近似計算が必要になります。近似計算が必要な場合、問題に出てくる物理量の大小の条件が明示されることが多いため、状況と大小の条件を結びつけつつ近似計算にも慣れることが重要になります。
過去問対策
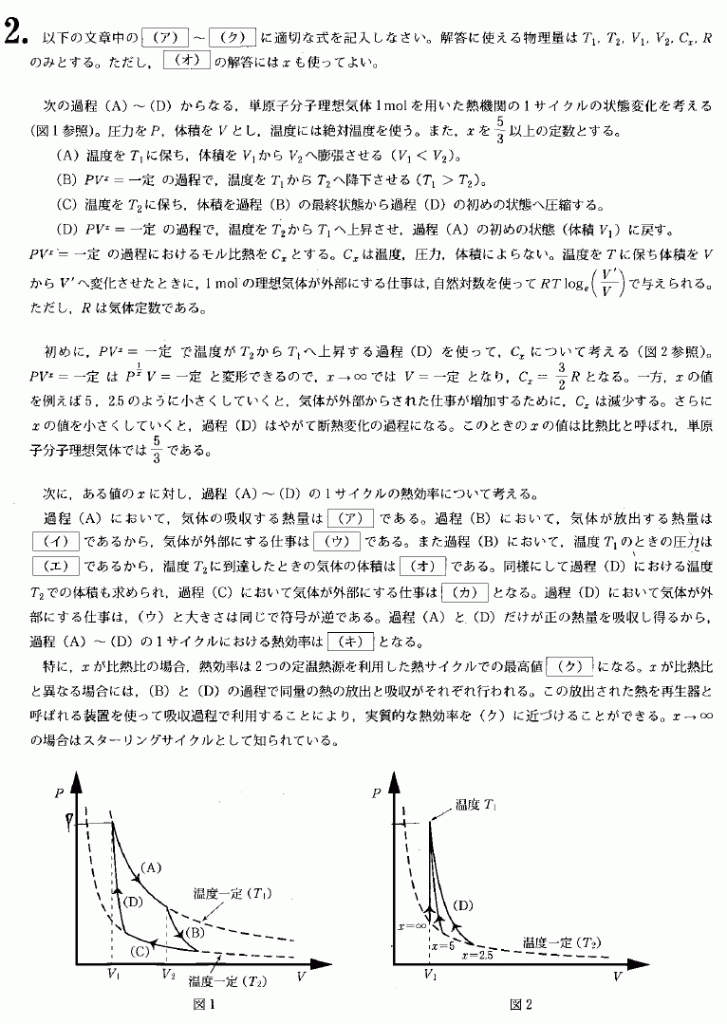
サイクルの問題です。まず各点での状態方程式を立てます、(ただし![]() 以外は自分で設定した)
以外は自分で設定した)
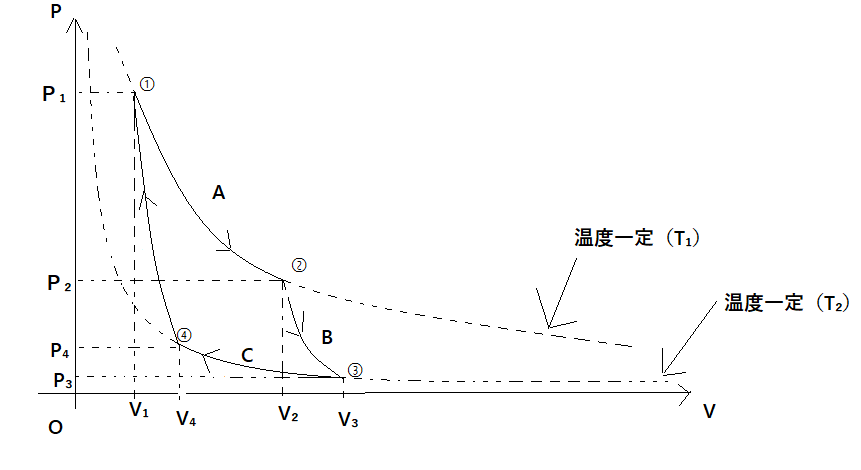
➀:![]()
➁:![]()
➂:![]()
➃:![]()
∴![]() 一定なので状態方程式を用いて以下のよう変形できます。
一定なので状態方程式を用いて以下のよう変形できます。
![]() 一定(∵Rは定数)・・・()
一定(∵Rは定数)・・・()
これを使って自分でおいた文字を問題文に書いてある式で書き直します。
![]() ・・・()
・・・()
![]() ・・・()
・・・()
![]() ・・・(****)
・・・(****)
(ア)過程(A)について、熱力学第一法則より
![]()
![]()
途中の式変形は、等温変化である(ΔU=0)と問題文に書かれていることを用いました。
(イ)は今回吸収した熱量を正で考えているので、放出した熱量は負になります。
![]()
(ウ)熱力学第一法則より
![]()
![]()
![]()
(エ)、(オ)
![]() のときの圧力は➁の状態方程式を使えば
のときの圧力は➁の状態方程式を使えば
![]()
温度![]() に達したときは(**)のときなので
に達したときは(**)のときなので
![]()
(カ)問題文の条件を使うと
![]()
(キ)
![]() です。
です。
これより熱効率をηとすると定義より
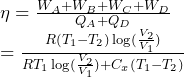
(ク)問題文よりxが比熱比のとき断熱変化になるので![]() となります。
となります。
よってηは、
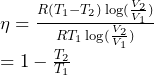
となります。

















Published by