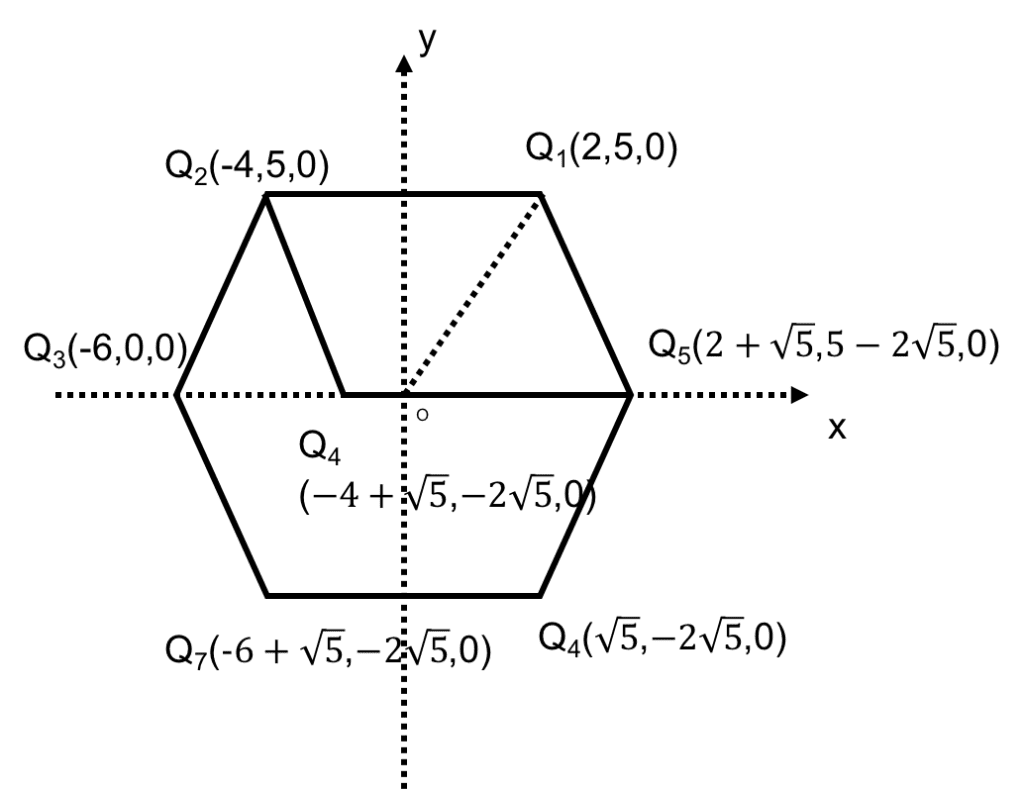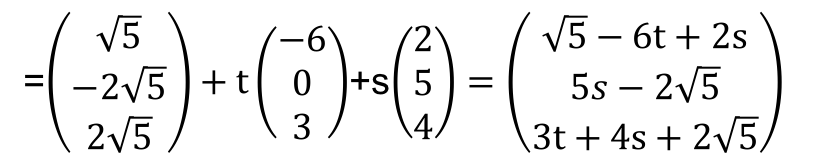慶應義塾大学理工学部が2/12に入試を迎えました。 このブログ記事では英語の問題を分析していきます。 ページ目次2024年慶應義塾理工英語全体講評2024年慶應義塾理工英語大問12024年慶應義塾理工英語大問22024年慶應義塾理工英語大問32024年慶應義塾理工英語大問42024年慶應義塾理工英語
- …続きを読む
- 慶應義塾大学理工学部が2/12に入試を迎えました。
このブログ記事では英語の問題を分析していきます。
[toc]2024年慶應義塾理工英語全体講評
昨年度出題されていた要約問題を用意していた人は肩透かしを食らったかもしれません。
全体としては、問題が減ったことにより昨年度よりも解きやすくなりました。和文英訳については、昨年度も出題されていたので準備していた人は多いので、問題はないでしょう。
[toc]
慶應理工は解き方に少しクセがあるのですが、
ちゃんと勉強していた人であれば、高得点を取ることは十分に可能になっています。解答作成には万全を期していますが、間違えている可能性は十分にありえます。速報ですので、参考程度に留めておいてください。少しですが解説・考え方も載せていますので参考にしてください。
重要:大学側から配点が公式に発表されてませんので、どれくらいあっていたら合格できるかはわかりません。2024年慶應義塾理工英語大問1
[1]
(1) 1
(2) 1
(3) 2
(4) 5
(5) 1
(6) 3
(7) 4[2]
(1) 5,overwhelming
(2) 4,hopelessness
(3) 5,responsible
(4) 3,destructive
(5) 2,marginalizagion
(6) 3,indadequacy
(7) 5,isolated
[3]
(ア)1, across
(イ)3, over
(ウ)5, with
(エ)4, toward
[4] 1,7[5]1,2,5,8
大問1の解答根拠
[4]
when human activities is having devastating consequences for life[5]
1,Another pandemic we face today is social injustice; the dehumanization and ( 5 ) that emerges from in-group domination ( Y ) out-groups that are subordinate in the social hierarchy.」
選択肢1について、文章は「他」として認識される人々に対する不正義、すなわち社会的不正義について言及しています。
2,A fifth pandemic is of attention addiction, the draw of our attentional focus ( x ) compelling states of endless comparison and competition and the ensuing feeling of ( 6 ), inferiority, and incompleteness.」
選択肢2に関しては、注意力を保持し、制御することの困難さ、つまり注意力の中毒について言及されています。
5,the modern cultural, or what some might call Western, view of an ( 7 ), separate identity—the “solo-self”.」
選択肢5は、西洋の文化的な観点からの独立した自己、すなわち「ソロ・セルフ」の概念について述べています。8,「A fourth pandemic is of misinformation and polarization, made rampant ( ^ ) the internet’s capacity to create self-sustaining bubbles of isolated information sharing.」
選択肢8は、インターネットが生み出す誤情報や極端な分極化による社会的分裂について言及しています。3,人間と動物の関係については、文章では言及されていません。
4,見知らぬ他人への共感やつながりについては、文章では直接的には言及されておらず、該当する部分がありません。
6,西洋資本主義の広がりについては、文章では言及されていません。
7,生命の神秘の解明に関しても、この文章では言及されていません。出典
Daniel J. Siegel, “IntraConnected”
2024年慶應義塾理工英語大問2
[1]
1,5
2,2
3,5
4,1
5,1
6,1
7,3
8,1[2]
X:2
Y:1[3]
(ア) 2. minimal
(イ) 2. contrast
(ウ) 3. righteously
(エ) 1. hold
(オ) 2. redefine
(カ) 4. take into account
(キ) 4. thereafter
(ク) 2. gotten away with
(ケ) 2. essential
(コ) 4. one出典
Arthur C Danto “What Art is”
大問2の解答根拠
[3]
(1) 2. minimal
根拠: “Plato was mainly negatively interested in art, since he was attempting to… and was eager to get rid of the artists on the grounds that art was of minimal practical use.”(2) 2. contrast
根拠: “In his view, what artists created were mere imitations of the real world, which had no practical use. In contrast, philosophers reigned the realm of human intellect…” この箇所では、芸術家と哲学者の間の対比を強調しており、「contrast」が適切です。(3) 3. righteously
根拠: “…philosophers could teach and serve as rulers not susceptible to corruption.” この文脈で「righteously」が適切で、「corruptionに染まらない」ことを意味する。(4) 1. hold
根拠: “Plato’s definition of art remained in place, with little to argue about until it stopped capturing the seeming essence of art.” この文脈では「hold」が「当てはまる」という意味で適切。(5) 2. redefine
根拠: “…in order to get a definition better than Plato’s you have to look to more recent artists…” これは「再定義する」ことを示唆している。(6) 4. take into account
根拠: “…you have to look to more recent artists…” これは「近代のアーティストを考慮に入れる」ことを示唆している。(7) 4. thereafter
根拠: “…that took place in France, mainly in Paris. In my view, to get a definition better than Plato’s you have to look to more recent artists, since they are most likely to subtract from their theories properties that were earlier thought to be essential to art, like beauty.” この文脈では「その後」という意味の「thereafter」が適切。(8) 2. gotten away with
根拠: “…art in recent times has gotten away with such concepts as beauty and imitation…” これは「避ける」または「取り除く」という意味で適切。(9) 2. essential
根拠: “…properties that were earlier thought to be essential to art, like beauty.” この文脈では「不可欠な」という意味の「essential」が適切。(10) 4. one
根拠: “Art, for one thing, has the power to touch people’s hearts.” この文は「一つの点において」という意味合いで使われており、「one」という選択肢が適切です。2024年慶應義塾理工英語大問3
[1]
(1)3
(2)3
(3)1
(4)2[2]
(1)9
(2)4
(3)8
(4)5
(5)8
(6)7
(7)6
(8)9大問3の解答根拠
[1]
(1) “you’re a sight for sore eyes”
辞書的な意味:非常に会いたかった人に会えて嬉しいという感情を表現するフレーズです。
用例:After a year of being abroad, seeing my family again was a sight for sore eyes.(2) “the green-eyed monster”
辞書的な意味:嫉妬を象徴するフレーズで、シェイクスピアの「オセロー」で使われたことで知られています。
用例:When he saw his ex-girlfriend with someone else, the green-eyed monster reared its ugly head.(3) “reading too much into”
辞書的な意味:実際の意味以上に深く解釈すること、または過剰に分析することを意味します。
用例:I think you’re reading too much into her comments; she probably didn’t mean anything by it.(4) “rings a bell”
辞書的な意味:聞いたことがある、どこかで見たことがある、またはなんとなく覚えているという状態を表すフレーズです。
用例:The name doesn’t immediately come to mind, but it certainly rings a bell.[2]
1,Didn’t get a ( 9 ) wink of sleep on the plane.
「一睡もできなかった」を意味する一般的な表現は “didn’t get a wink of sleep” です。
2,”Ms. Yagami ( 4 ) picked up on my suspicions.” が適切です。
“picked up on” は「気づく」や「察知する」という意味で使われ、この文脈では、Ms. Yagamiが主人公の疑念に気づいたことを示しています。
3,I felt like the ( 8 ) third wheel during the entire drive to the campus.
“third wheel” は、「余計な人」という意味で、ここでは主人公が八神さんとスタンフォードとの間に挟まれて不要な存在のように感じている様子を表しています。
4,Situation is ( 5 ) serious.
文脈から、主人公は自身の立場や将来の決断(プロポーズ)について深刻に考えていることが伺えるため、”serious” が適切です。
5,It may be time to ( 8 ) pop the question.
「プロポーズをする時が来たかもしれない」という意味で使われる一般的な表現は “pop the question” です。
6,At the airport I tried to ( 7 ) play the situation down.
「状況を軽く見せようとした」という意味で使われるのは “play the situation down” です。
7,I can smell it a ( 6 ) mile away.
「何かをはるか遠くから感じ取る」という意味で使われる表現は “smell it a mile away” です。
8,Maybe it’s just the jet lag talking. I’ll see things more clearly after a good night’s ( 9 ) rest.
「良い休息を取ればもっとはっきり物事を見られるだろう」という意味で使われる表現は “a good night’s rest” です。2024年慶應義塾理工英語大問4
(1) 6
(2) 5
(3) 6
(4) 42024年慶應義塾理工英語大問5
Some people are continually called back to their hometown, while others feel they can never go back.
Some are always drawn back to their birthplace, whereas others believe they cannot return.
For some, the hometown exerts a constant attraction, but for others, returning seems out of reach.
Some people are constantly pulled back to their hometown, while others feel that they can no longer return there.
Some individuals feel a continuous pull towards their hometown, while others feel it’s impossible to return.
There are those who are forever beckoned back to their place of origin, and those who think they can’t make their way back.
Some feel an unending tug back to their hometown, while others consider it a place they can no longer visit.
A number of people experience an ongoing pull to return to their hometown, whereas others view it as a chapter permanently closed.
For some, the hometown calls them back time and again, while for others, the path back seems permanently closed.
Some are perpetually lured back to their birthplace, while others see it as a place they’ve left behind for good.
Some people find themselves repeatedly returning to their hometown, while others feel barred from going back.
2025年慶應理工学部を受ける人はどうするか?

慶應理工学部は割と単語勝負なところがあるので、
英検準1級までの単語を取りこぼしのないように覚えてもらうことが肝心になってきます。単語がわかれば問題を解くスピードをかなり縮めることができるので、短い時間で高得点を取ることができます。
また、今年の大問2にでたような要約問題は毎年でているので、この問題は得意になっておく必要があります。
早稲田理工と比べると英語の難易度はだいぶ下がるので練習次第で高得点を取ることが可能になります。
お気軽にご相談ください。














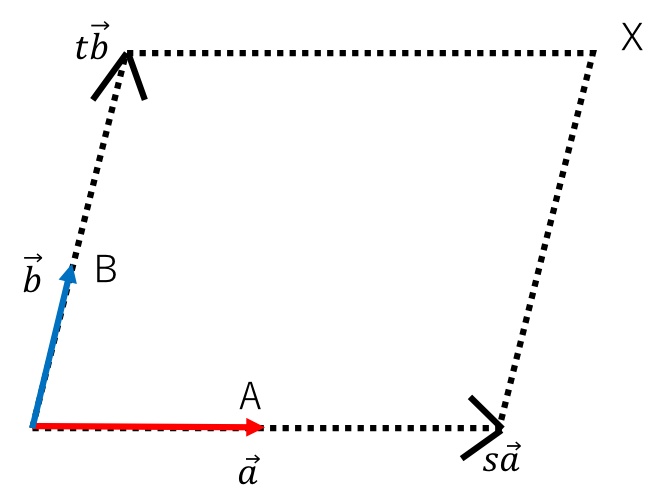
 図2
図2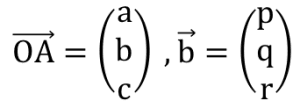


 なので、線分OA上にz=tを満たす点A’が存在する。
なので、線分OA上にz=tを満たす点A’が存在する。 と表せる。
と表せる。 図4
図4
 で線分OA上にz=tを満たす点が存在しなく、線分AB、AC、OCを共通にもつ。
で線分OA上にz=tを満たす点が存在しなく、線分AB、AC、OCを共通にもつ。 ・・・(タ)
・・・(タ)
 図6
図6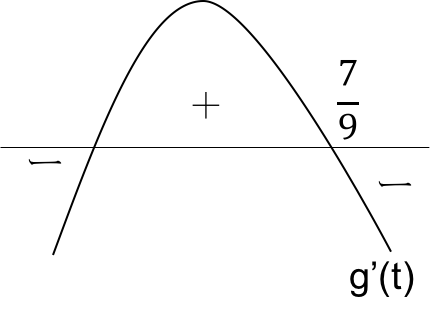 図7
図7
 とおける。(i)より
とおける。(i)より ・・・(ソ)
・・・(ソ)
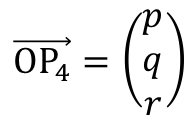 とおくと、
とおくと、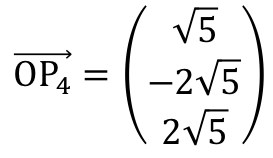 ・・・(タ)
・・・(タ)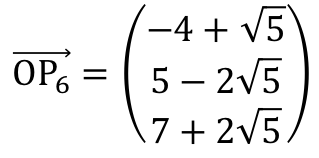 ・・・(チ)
・・・(チ)