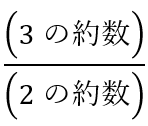
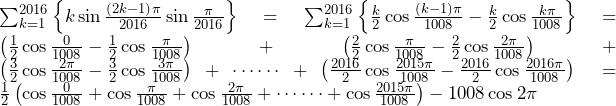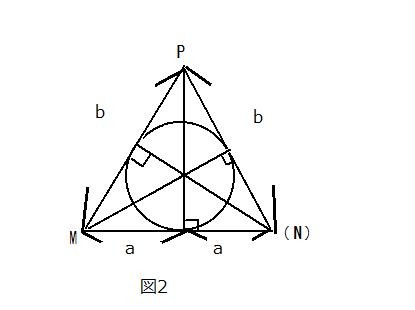早慶・難関国立・難関私立大学を目指している受験生が当塾でどのように最速で数学を学んでいるのか、その勉強方法をお伝えします。
勉強はただやみくもに時間ばかりかけても成績は上がりません!適切な勉強方法、計画を建てて何をいつまでに行うのか?を決めておく必要があります。当塾で指導している最速で効率的に数学の成績をあげる勉強方法の一部をお伝えいたします。
<このページの読み方>
▶基本的に全部読んでいただくことを推奨しますが、数学ができない原因を知りたいのではなく、とにかく数学ができるようになるためにどうしたら良いのかを知りたい方は「応用編(アウトプット)」をお読みください。
▶必要参考書一覧も最後に載せてあります。
*下記クリックすると、その部分まで飛んでいきます。
[toc]
なぜ数学が嫌いになるのか?
他の科目と比べてなぜ数学きらいが多いのか?まずはそこから考えてみます。当塾には全国から数々の数学嫌いが集まってきます。数学の勉強法の前にまずどのような理由で数学ができなくなっているのかということとその簡単な解決策をお伝えしていきます。
ケース① 圧倒的に計算が遅い
時間があれば、答えまでたどり着くんだけど。。。いつも最後までいけません。
生徒と授業をしていて問題を授業中に解いてもらう時があるのですが、計算の仕方が悪いのか,なかなか答えがでません。通常の生徒であれば、即答レベルの計算であっても、10秒近く考えてしまうことが多くなります。こういうケースで本人に聞くと「問題はわかっている。」とのことが多いです。ですが、一向に答えまでがでてきません。こうした生徒の場合ですと数学的主張を解釈する以前の段階で計算などができなくなります。そこでストレスがたまり、問題が解けるより前に数学が嫌いになってしまうのです。一度数学が嫌いになってしまったら数学が嫌いになってどんどんできなくなってしまうのです。
こうした生徒の場合はまずは四則演算が大事です。毎日15分程度で良いので、毎日積み重ねて行くことによって四則演算を速くしていきましょう。計算練習の高速化は、ある種頭の回転の速さにもつながります。
また計算が遅い、できないとその時点で理系終了で文系しか選択肢がなくなります。別に文系が悪いのではなく、選択肢がはじめから存在しないというのはツラいですね。このレベルで躓いている人は毎日繰り返し計算練習を行う習慣をつけていきましょう。3,4ヶ月もすれば圧倒的に早くすることができます。
下記教材は分数といった小学校レベルから計算を開始していくため、久しく数学から離れていた医学部再受験の方であっても問題なく理解できるでしょう。
数学勉強の初期段階では難しい問題を唸りながら行ってもできるようにはなりません。基本的な計算練習をひたすら行って、無意識でも計算の意味が具象化して理解できるレベルに持っていけるレベルまで持っていきましょう。
▶0からやりなおす中学数学の計算問題の使い方はこちらから
ケース②公式の意味がわかっていない
数学なんて、公式にいれればいいだけで簡単な科目でしょ。
ケース①と同様に多いのが、この公式の意味が理解できてないという場合です。このケースの場合は逆に計算は速いという子に多いです。おそらく、計算練習をたくさん積んできたのでしょう。前述のように計算は数学ができるためには大事な部分です。
ですが、意味の理解できてないことをひたすら繰り返しおこなっていてはいつまで経っても数学はできるようにはなりません。
数学には”定義”という、どんな場合でも適応する言葉での約束事が存在します。この定義からなぜこの公式が成り立つのか?という部分を考えることができる(理解できる)ようになるのが、<入試では実際に自分の力で導けるように!>、重要です。公式を意味もわからずあてはめていくだけの勉強ではいつまで経っても数学はできるようになりません。
上位の大学に行きたいのであれば、
公式を見たらなぜこの公式が成り立っているのだろうか?という部分を考えるようにしましょう。
例えば、相加相乗平均と不等式なら証明は5個以上挙げられると良いです。
ケース③問題を丸暗記する
数学は暗記です。チャートを丸暗記すれば余裕ですよ。
ケース②と似ているのですが、まだ概念や公式の意味を理解してないのに青チャートやフォーカスゴールドを行う子に多いケースです。意味合いがわかっていないのに網羅系問題集を使って、とにかく問題のパターンを覚えてしまおうという考え方なのでしょう。学校の定期試験であればその方法は使えるかもしれません。ですが、入試というのは、基本的に(例外はあります)これまでにでたような問題はでてきません。
ですから、意味もわからず問題を覚えるというのは愚の骨頂なのです。
青チャートを覚えればできるって話を聞いたことがありますがどうですか?
和田秀樹氏が提唱していた青チャート勉強法が未だに根強く残っているのか?青チャートさえ覚えれば東大でも受かる!と思い込んでいる人が多いようです。もちろん、青チャートの内容を理解して自身の頭のなかでパターン化されているのであれば問題ないでしょう。
ですが、多くの勉強ができない子の場合、
問題自体を覚えているだけで少しでも数字が変わったら応用が効かなくなってしまうレベルの丸暗記をしています。もちろん、このような覚え方では「丸暗記数学」となってしまい、いつまでたっても数学ができるよになりません。
こうした場合には、論理展開を日本語で考える癖をつけるのが良いでしょう。
なぜその次の式に展開したのか?というのがわからなければいつまで経っても自分自身で再現することができないので、できるようになりません。
また公式の意味や定義が頭の中でしっかりと考える癖ができていれば、問題のパターンを覚える暗記に入っても頭の中で整理できるようになります。
ですが、何も前提がないまま暗記をしてしまっては、どのように公式ができているのか?ということがわからないため、いつまで経っても理解ができるようになりません。
その結果、成績が上がらないということにつながるのです。
ケース④わからない数式が出てきた瞬間に考えない
こんな式展開見たことないからほったらかし・・
最後のケースですが、これはある程度数学の範囲を終えた段階での話ですが、、
自分のわからないことになった瞬間に沈黙して解答にも何も書かない。という場合です。
このケースの場合だと、数学の偏差値60までは順調に伸びていきます。
ですが、それ以上となると難しいでしょう。
よくよく文章を読んでみれば自身がこれまでにやってきたこと相違ないことがほとんどです。
このような場合は文章を噛み砕いて、かつイメージ化して理解する癖、具体的に考えるとどうなるだろうか?ということを考えられるようになりましょう。
ケース③でも述べましたが全ての問題のパターンを知っているということは難関大学においては多くないでしょう。
ケース⑤計画の立て方が間違っている
過去問を解きまくればそのうちできるようになるでしょ!?
ケース②と似ていますが、「先に進まなきゃ・・」と焦ってムリな計画をたてるがあまり考えることを放棄することになってしまい、結果的に成績が上がらなくなるといういことになってしまうのです。
たとえば三か月で青チャートを終わらせると決めたとき、問題数ごと単元ごとにある程度細分化した計画(1週間でどこまでやるかなど)を立てると思います。
決められた時間で大量の問題を解かなければいけないので分からないとすぐ答えを見てしまっていませんか?すぐ答えを見て何か得られるものはあるのでしょうか?もちろん、この方法では思考力は身につきません。
問題を自分の頭で解けるようにしてから、量をこなしたり、スピードを求めるようにしましょう。
パターンを覚えていてくというのは成績を上げていく上では大事です。ですが、自分の覚えているものを使って“考える”というプロセスを経ずして成績を圧倒的に上げることは不可能です。
最低でも1問に30分はかけて1問と向かい合い、自分の頭でじっくり考え、解ける喜びを感じてみてください。
急がば回れとはよく言いますが、これは数学においても当てはまります。
基礎
数学ができるようになるためには、ただ単に問題のパターンを覚えるというだけではできるようにはなりません。上記で見てもらったように、多くの数学ができてない学生というのは、表面上の数値のみを暗記しているために数学ができなくなってしまっています。上記のようなことが発生しないようにするために、当塾では、基礎概念を把握→高速化→運用というプロセスを行っております。下記ではそのプロセスを詳しく説明していきます。
基礎の基礎<中学数学について>
高校数学を行う前に中学数学が理解できているかどうかを確認しましょう。特にこれまでの指導の中だと帰国子女で数学を全く勉強してないのに、帰国子女枠でレベルの高い進学校に入ってしまった学生、医学部志望など社会人になって学生時代数学は得意ではなかったけれど、勉強しなくてはならなくなった人の場合は中学数学から確認する必要があるでしょう。
中学数学の段階で公式の意味を理解していないで計算練習ばかり繰り返していてはできるようになりません。
概念把握
数学における概念把握とは、「座標軸上での状態」と「四則演算の行い方」があたります。それぞれの分野において、何も考えずにいきなり公式を覚えるのではいけません。新しい分野には入った場合には常に「座標軸上での状態」と「四則演算の行い方」を確認しながら理解していきましょう。
その上で、各分野で出てくる公式の証明が行えるようになることがあるでしょう。公式の証明をできるようにしておくというのは、その公式をなぜその部分で使用するのか?の意味が理解できません。ですから、全ての公式についてすぐに導出できるようにしておくべきでしょう。
ただし、勉強の初期段階で公式が出てきたら、毎回導出ができるようにしていくということを行っていくと進みも悪いため、やる気がおこならない可能性があります。そのため、勉強の初期段階では、この公式はどのように成り立っているのか?ということを考える癖はつけつつ、公式を使って問題を解いてみるというのが先で良いでしょう。
下記では実際に公式の証明を使用して、公式をどのように覚えていったらよいのかをお伝えしていきます。
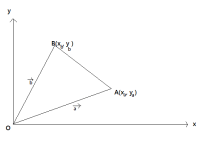
ベクトル 内積の公式を図形的に考える
以下の様な図を考えたとき、

△OABにおいて余弦定理より




∴
記号を日本語で噛み砕く
公式の意味を数学特有の記号Σ、∫、lim、fの操作の意味を日本語で理解しておくことは重要です。この辺りは英語の単語を覚えるのと同じです。単語の意味がわからないと英語の文章を読むことも書くこともできないのと同様に、記号の意味をわかっていなければ使うことはできません。私たちはdogと見た瞬間に、実際に人それぞれどのような犬を想像するかは違いますが「犬」を頭の中で想像します。数学の場合は、記号に対しての動作が決まっていますので、数学特有の記号を見た瞬間に皆同じことを考えることができるのです。
ですが、数学ができない人は記号を見た瞬間に思考が停止してしまっています。
たとえば、

この数式の意味はkに1からnまでいれて、それぞれ足しなさいという意味です。
つまり

ということをΣを用いて書いているだけなのです。このような理解を記号を見た際にすぐにできているかどうか?というのが大事です。
坂田アキラ先生のシリーズではそうした記号の使い方を様々な例を活用してわかりやすく説明しています。数学が苦手な方はまずはこちらのシリーズを読んでみると良いでしょう。
▶『坂田アキラの面白いほどわかる数学シリーズの使い方』の詳しい使い方こちら
池田洋介先生のシリーズもイラストを使ってあるのでまったくの初学者でもわかりやすく解説してあります。数学2Bは苦手な学生が増える分野なので、苦手だ!と感じた瞬間に取り組むと良いでしょう。
▶『数学ⅡBが面白いほどわかる』の詳しい使い方はこちら
学校で一度勉強をした範囲だけど公式が丸暗記になっていたり、問題は一度覚えてやってみたけど何かできないな。。という方は『元気が出る数学1A2B』を勉強すると良いでしょう。上記2冊はわかりやすさでも随一の教材ですが、
▶『元気が出る数学1A2B』の詳しい使い方はこちらから
計算練習で高速化
概念をつかみ、公式を理解できたら高速でその概念、公式を正確にかつ高速で使えるようにしていきます。このレベルまで来て役に立つのが計算練習になります。公式を実際に使って、四則演算、座標平面上の動きを理解していきながら、計算練習を積んでいきましょう。
▶『合格る計算ⅠAⅡB/Ⅲ』の詳しい使い方はこちらから
運用力×高速化
各分野での計算練習を積んで四則演算、座標平面上での動きの意味がわかったのであれば、実際に問題を解いていきましょう。このレベルで大事なのは、問題文の内容を読んでいる際に思考停止せず、数学的な理解ができているかどうか?ということです。
上記概念理解や計算練習ができてない段階で問題を解くことを行ってもあまり意味がありません。標準問題精講シリーズは他のシリーズは難しいですが、数学1Aに関してはレベル感も偏差値50~55程度の学生でも理解できかつ、解説もわかりやすく、どのように問題を解いたらよいのか?の着眼点も用意されています。
▶『標準問題精講』の詳しい使い方はこちら
『マセマ合格数学シリーズ』は着眼点、式の展開が丁寧なので独学でも問題なく勧めることができるでしょう。標準問題精講の2B3は難し目なので、合格シリーズがその代用になっていきます。入試レベルの典型的な問題が多いので、全ての問題に対して解法を自身の手で実際に最後まで導けるかどうか?という点が大事になってきます。
▶『マセマ合格数学』の詳しい使い方はこちらから
入試準備のレベルの基礎レベルとしては、『1対1対応の数学』までできていれば、基本的な数学の入試問題は対応できます。1対1対応の数学はこれまでの教材と比べると、式の展開もわかりづらい可能性があります。
また、1対1対応の数学独特の表現があったりもするので、その理解をするのが初学者にとっては難しいです。ですが、これまでの『マセマシリーズ』や『標準問題精講』がただの暗記でなく理解ができている上での運用ができているのであれば、問題なく理解ができてきます。
このレベルをクリアできれば入試問題の理解ができるようになるのも後もう少しです! 頑張りましょう!
▶『1対1対応の数学』の詳しい使い方はこちらから
できる人とできない人の差とは?
問題を理解している時に数学ができる人はどのように理解しているのか?、数学ができてない人はどのように理解しているのか?という差をご説明します。勉強している最中にできない思考に陥らないようにしましょう。
[su_box title=" 早稲田大学2016年度 理工学部 数学 大問Ⅱ(1)" style="glass"]

[/su_box]
できない人はこう考える!
■図を書かない(イメージできない)
数学ができない人ほど、図を書かない人が多いです。図形問題の時は必ず図を書いて考えましょう。実際に図を書いていくことで、直感的にこの図形はこの硬式を使えばいいんだなというのが見えてきます。
できる人はこう考える!
■図を書く
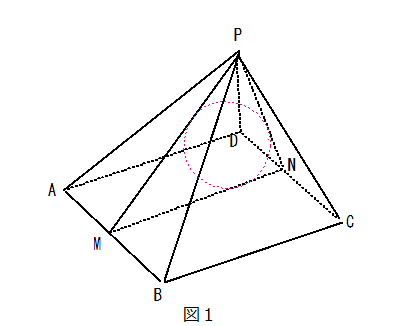
図を書くのは当然として、立体の問題を解くときに、断面図まで書けるかが1つの差をつけるポイントです。


図1:全体図、図2:断面図
このような断面図にすると、内接する球の半径は、二等辺三角形△PMNに内接する円の半径と同じであることがわかります(Nは線分CDの中点)。ここで、直線と円の接点において、接点と円の中心を結ぶ線分は直線に垂直になります。よって、球の半径をrとすると、△PMNの面積は

で表されます。また、△PMNはMNを底辺とする二等辺三角形であるので、MNを底辺とした時、高さは

になります。よって、△PMNの面積は

のようになります。この二通りで表された△PMNの面積は等しいので、

の式が成り立ちます。よって、球の半径は

で表されます。
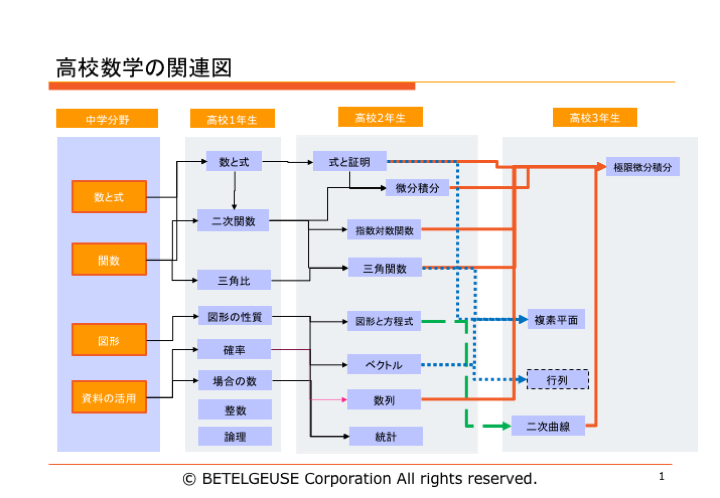
高校数学の流れを考える

数学を苦手になる理由として、次から次へと新しい分野を行っていくために今何を行っているのか?、前の分野で使ったことは使えないのか?という錯覚に陥ってしまいます。なぜならば、学校で習う数学の順番というのは特に意味がなく、昔からこの順番で習うと決まっているから、現在の順番で学んでいるのです。それぞれの数学を学ぶ順番の意味合い、他の分野との関係性を理解していくことが大事です。
特に理系の場合は、数3の微分積分が速く正確にできるようになるということが絶対条件としてあります。この分野までにいかに効率的に行っていくかどうかというのが高速理解のための必須条件となります。数学3の微分積分というのは計算自体は複雑で難しいですが、問題自体のパターンは少なく問題数さえこなせれば得意になることが可能です。得意になるためには問題数をこなしておくという前提条件があります。問題数をこなすためには、いかにして早い段階で数学3まで到達することができるのか?という点がポイントになります。
当塾では、効率的に効率的に指導を行っていくために順番を改変して指導を行っています。数学1A→2Bという順番に勉強をしていっては数学ができない人にとっては様々な分野が入り交じるため成績を効率的に上げるためにはよくない順番です。
また、各分野についての関係のイメージを持っておくことも大切です。
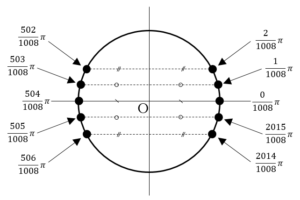
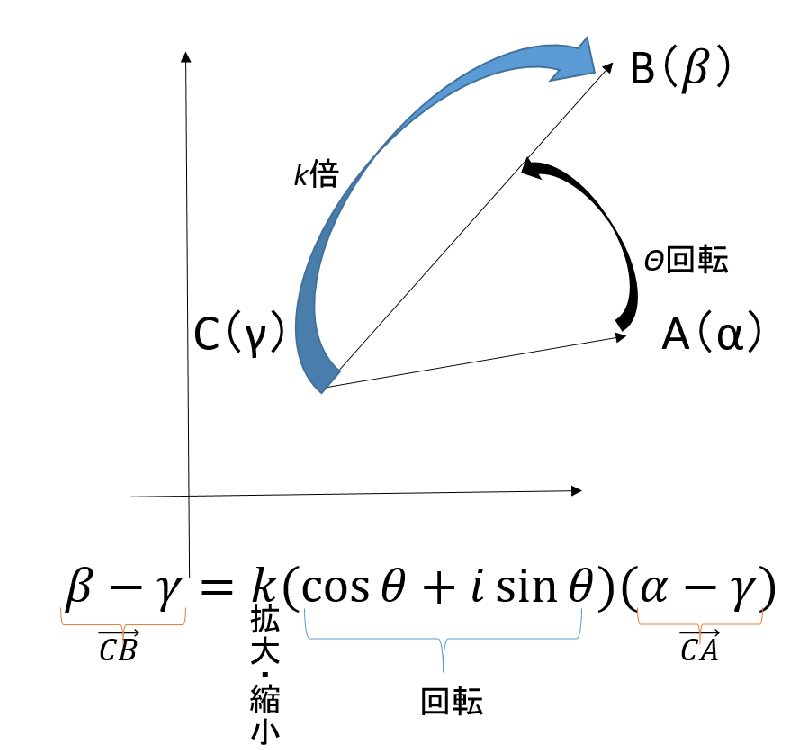
例えば複素平面で考えてみましょう。下記の図を見てください。
回転と拡大縮小という考え方はイメージがつきづらいですが、三角関数との関係やベクトル的なイメージを持っていると随分考えやすくなります。
数学の勉強というのは、正しく勉強すれば誰でも成績を上げることが可能です。成績が上がらないということは何かしらの理由があります。数学の成績が上がらないで困っている方はこちらからご相談ください。
文系数学の各々の分野の勉強の仕方
理系数学と文系数学は範囲が異なります。範囲が異なるからといって簡単になるといわけではありません。
ただ闇雲に勉強をしていても成績は上がりません。
それぞれの分野でポイントを抑えて勉強を進めていくことが大事です。下記で、文系数学でどのように要点を抑えて勉強をしたら良いのかをお伝えしていきます。
<二次関数>
二次関数単体の問題は少ないのですが、最終的に最大最小の問題を二次関数で行うなど道具としての面が強いです。
軸や範囲による場合分け、解の配置の二つが主にできれば差支えないので、完璧に使えるように演習しておきましょう。
<不等式>
単体で不等式が出題されるのは阪大など一部に限られますが、相加相乗平均の不等式、再配列不等式、シュバルツの不等式、チェビシェフの不等式くらいは当たっておいてほしいところです。
もともと不等式の議論というのは、不等式の変形で同値性が崩れやすく、必要十分に気を配りながら解いていく必要があり、極めて難しいです。
不等式は正負も大事になってくるのでよく理解しておきましょう。
<場合の数>
この分野は問題によっては小学生でも解けますし、これまでの蓄積の面が強いのですが、勉強のしかた次第で難しい問題でも解けないわけではありません。
樹形図、表を駆使して漏れや重複なく数え上げられるように訓練しましょう。
1000通り前後、例えばさいころ四つ投げた36×36=1296通りくらいは手計算で数え上げられるように鍛えましょう。
また有名な対応づけは十分理解し、それを応用できるようにしておくと強いですし、センスが身に付きます。
巧妙な解法は思いつかないから無駄という人がいますが、本番でエレガントな解法を思いつくには普段から巧妙な解法に触れていなければ、無理な話です。
短時間で習得できる分野ではないので長いスパンを設けてじっくりと向き合ってあげてください。
<確率>
場合の数とやることは大差ないですが、場合の数と致命的に違うのは、同様に確からしいに気を配る必要があるということです。
あとは条件付き確率ですが、ベン図を使うと理解しやすいので参考にしてみてください。期待値は範囲外ですが面白いので触れてみることをおススメします。
確率漸化式が早慶をはじめ、難関大では多く出題されるので対策が必要です。
すべての確率の和は1になることは忘れやすいのですが、これが鍵になる問題も多いので、頭の片隅にとどめておきましょう。
<整数>
この分野は好き嫌いが分かれますが、大学受験レベルだと、因数に注目する、不等式などで範囲を絞る、余り(mod)を考える、の三本柱を組み合わせて解けるので自分の頭でじっくり考えるのが大事です。
ガウス記号やペル方程式、不定方程式など頻出問題には当たっておきましょう。
大学ごとで問題の傾向が分かれるので過去問を見て、似たような問題に当たって鍛えておきましょう。
文系でも早大商学部などは、難度の高い整数問題を出したりと油断できません。
<代数、方程式>
東大、京大などの難関大になると、時々難問で出るのですが、この分野は余裕があればやるくらいで良いと思います。
結構知識の面も強いので、数学でやることなくなった人は趣味程度にやると楽しいです。
チェビシェフの多項式、ラグランジュの補間公式、プラーマグプタの恒等式などは知っていれば便利なので、余裕があれば触れておくと面白いと思います。
<三角関数>
ラジアンの理解が甘いひとがときどきいて、sin1がどういうことを意味しているのか分からないというのは困るので定義をちゃんと理解しておきましょう。またこの分野も他の問題と融合で出るので、加法定理、和積は自由自在に行き来できるようにしましょう。倍角は3倍角くらいまで暗記しておくと便利です。
また最大最小や領域などで最終的に三角関数の処理になることがしばしばあるので計算で間違えることのないように反復練習しておきましょう。
<対数>
文系だとlogの方程式を解いたり、不等式を扱うことが多いと思いますが、何桁か問われたりすることもたまにあるので底が何でもしっかりと扱えるようにしましょう。
また対数の四則演算は計算演習が甘いと間違えことも多いので無意識でもできるレベルまで計算演習をしておきましょう。
<数列>
等差数列、等比数列の一般項や和を理解しているのはもちろんのこと、添え字にその都度気を配ることは大事です。
また和をとる=差を作るということは極めて大事なので、ここでは詳しく説明しませんが、よく考えておきましょう。
難関大では、偶奇で一般項が違かったり、ガウス記号がついていたりと面白い数列が出題されますが数列として特殊な知識を使うことはありません。
整数の見方も大事にしながら理解を深めていきましょう。
<ベクトル>
平面、空間上の状態を表現するための新たな道具がベクトルです。
慣れるまではなかなか掴みづらいのですが、大事になるのは一次独立、内積、単位ベクトルくらいなので、そこの概念はしっかりと確認しておきましょう。
平面は解けるけど、空間は解けなくなる人がいますがやることは変わらないので怯えないでください。
座標を置けばがんばれば解けますが、 計算量が大変になることが多いのでベクトルは大事です。
<座標>
座標の知識としては、点と直線の距離の公式、傾きはtanでとらえる、束の考え方、順手流・逆手流(通過範囲)が抑えられていれば十分でしょう。
円の考察が絡む問題も少なくないので接線や距離関係などにも一通り当たっておきましょう。
あとは軌跡を求めたり、最大最小の問題ができれば基本は大丈夫でしょう。
また図形的考察やベクトルを駆使して計算量を抑えるなど上手に考えていけるとよいですね。
逆に幾何やベクトルを座標で解くこともできるので計算力の増強は課題となるでしょう。
<微積>
数Ⅱの微積は問題のパターンが決まっていて、微分は関数の増減や、接線を求めるためのツール、積分は面積を求める道具としてしか考えていない人が多く、やり方だけ丸暗記している人も少なくないのではないでしょうか?
過去のセンター試験でも極限から問われるなどイレギュラーもあるので、文系でもしっかり微積の意味、定義を考えておきましょう。
また面積公式に頼っている人がいますが、1回は導出したうえで使いましょう。
一般化して自分で面積公式を作ってみたりすると勉強になりますし、理解が深まります。
また文系でも数Ⅲの範囲におけるある程度有名な積分はできたほうが有利です。
<複素数>
文系だと虚数解になることがあるくらいしか知らない人がいますが、複素数の四則演算に加えて、共役な複素数についても理解を深めておきましょう。
課程が変わり、理系に複素平面が追加されるのにつられて、文系でも複素数の出題が増えていますから要注意分野と言えるでしょう。
文系では、ベクトル、座標、積分の計算力があれば、有利なのでこの3分野は高速に処理できるようにしておきましょう。
Q&A
ここでは基礎的な数学部分について当塾に寄せられる質問をQ&A形式でお答えします。
学校で皆がチャート式を使って勉強しています。僕も真似して使っているのですが、正直答えを見ても理解できず、ただ暗記しているような気がします。これでも大丈夫ですか
暗記をしているだけでは、数学をその場しのぎの問題に対処することはできますが、圧倒的に得意にすることはできません。得意にするためには、概念を理解して上述したように数学を理解していく必要があります。特にチャート式は網羅系といわれるくらい問題数が多く、日本語での説明は皆無です。ある程度理解した段階で抜け漏れがないかの確認、問題数を稼ぐという意味合いで使用するのであればチャート式でも使いこなすことができます。ですが、数学が苦手でかつよく理解できてない段階でチャート式を使用するのはよくないです。情報量が多すぎます。
数学ができません。私は文系脳なのでしょうか? また数学的センスが無いのでしょうか?どれだけ学校でもらったワークを覚えてもテストの最中に忘れてしまったり、全然できません。このまえはテストの点数は一桁でした。現代文や社会は学年でもトップクラスでできるのですが、、、どうしたら良いのでしょうか?
まずは落ち着いてください。数学にセンスは必要ありません。現在数学ができてないというのは様々な原因が考えられますが、ワークをやってもできてないということはワークの内容が自身の言葉で噛み砕けてない可能性があります。数学は数を扱う科目ですが、根幹は日本語で理解ができるかどうかという点に絞られてきます。数式を見て、数式で理解をするのではなくて、日本語でどういう意味でいっているのか?、座標でイメージするとどういう意味になるのか?という点を理解していきましょう。またそれができないというのであれば現在行っていることの前提条件が抜けている可能性があります。特に、中学は数学ができたけど高校になったら数学ができなくなった・・という子は、中学は覚えるだけで対応していたという場合が多いです。これでは数学はできるようにはなりません。中学レベルの内容から日本語で噛み砕けるように勉強してみてください。数学は正しく勉強すれば誰でもできる科目です。がんばって下さいね。















 と平面
と平面 の交線
の交線 は,実数パラメーター
は,実数パラメーター を用いると,
を用いると,
 は,
は, を通り(
を通り( を代入),方向ベクトルは
を代入),方向ベクトルは である直線.
である直線. ……(答)
……(答) の半径を
の半径を とおく.すると,球面
とおく.すると,球面 の方程式は
の方程式は と表せる.
と表せる. と直線
と直線 が1点のみを共有するとき((23)~(27)について)
が1点のみを共有するとき((23)~(27)について) と交線
と交線 の共有点が1つのみとなるには,以下の
の共有点が1つのみとなるには,以下の に関する2次方程式
に関する2次方程式

 .
. ……(答)
……(答) と直線
と直線 が1点のみを共有するとき((23)~(27)について)
が1点のみを共有するとき((23)~(27)について) と交線
と交線 の共有点が1つのみとなるには,以下の
の共有点が1つのみとなるには,以下の に関する2次方程式
に関する2次方程式

 .
. である(複号同順).
である(複号同順).
 と直線
と直線 の距離は,三平方の定理より,
の距離は,三平方の定理より,
 を頂点とする三角形の面積は,
を頂点とする三角形の面積は,
 であるとき,
であるとき,

 ……(答)
……(答) は面内に直線
は面内に直線 を含み,かつ
を含み,かつ 依存性がないため,
依存性がないため, ……(答)
……(答) は面内に直線
は面内に直線 を含み,かつ
を含み,かつ 依存性がないため,
依存性がないため, ……(答)
……(答)






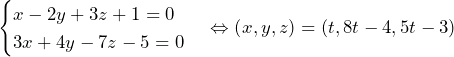
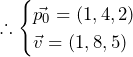 ……(答)
……(答)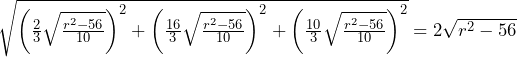
![Rendered by QuickLaTeX.com \int_{x_m}^{x_a+1}\left|m\left(x\right)-a\left(x\right)\right|dx=\int_{4}^{7}\left|x^2-8x+17-\left(\frac{1}{3}x^2-4x+17\right)\right|dx=\int_{4}^{7}\left|\frac{2}{3}x\left(x-6\right)\right|dx=\int_{4}^{6}\left\{-\frac{2}{3}x\left(x-6\right)\right\}dx+\int_{6}^{7}{\frac{2}{3}x\left(x-6\right)}dx=\left[2x^2-\frac{2}{9}x^3\right]_4^6+\left[\frac{2}{9}x^3-2x^2\right]_6^7=\frac{76}{9}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-f16c686959dba9c1141ca1d2b264f9d3_l3.png) ……(答)
……(答)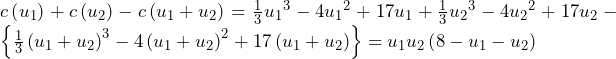 ……(答)
……(答)

 ……(答)
……(答)
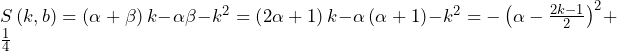
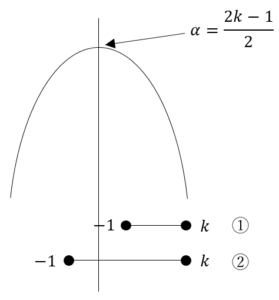
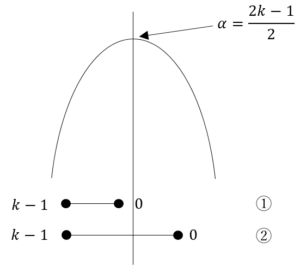
![Rendered by QuickLaTeX.com \int_{-1}^{-\frac{1}{2}}\left(-k^2-k\right)dk+\int_{-\frac{1}{2}}^{0}\frac{1}{4}dk+\int_{0}^{\frac{1}{2}}\frac{1}{4}dk+\int_{\frac{1}{2}}^{1}\left(-k^2+k\right)dk=\left[-\frac{1}{3}k^3-\frac{1}{2}k^2\right]_{-1}^{-\frac{1}{2}}+\left[\frac{1}{4}k\right]_{-\frac{1}{2}}^0+\left[\frac{1}{4}k\right]_0^{\frac{1}{2}}+\left[-\frac{1}{3}k^3+\frac{1}{2}k^2\right]_{\frac{1}{2}}^1=\frac{5}{12}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-e0c8bfe825912f02cafeb7f3d4b9999f_l3.png) ……(答)
……(答)