5分でわかる受験のキソのキソ | 【慶應早稲田専門対策】個別指導塾ヒロアカ

【物理】力の種類（力のつりあいその1）

2016.12.07

力は重力、摩擦力、バネによる力、張力などと様々な種類があるように思えますが、図示するときには忘れずにすべての力を書き込むのはそう難しくありません。力そもそも力とは、物体を変形させたり、運動させたり、回転させる原因となるものです。その単位なニュートン（N）で表され、ベクトルなので向きを持ちます。

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]問題でいつも力を図示せよ、っていう問題で１つくらい忘れちゃんだよな…。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]わかる！力って物体に触れてなくても働いてたりするしね。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]一体力ってどれくらいの種類あるんだ？[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]すごい数ありそう…。[/speech_bubble]
力は重力、摩擦力、バネによる力、張力などと様々な種類があるように思えますが、図示するときには忘れずにすべての力を書き込むのはそう難しくありません。

力

そもそも力とは、物体を変形させたり、運動させたり、回転させる原因となるものです。

その単位なニュートン（N）で表され、ベクトルなので向きを持ちます。

力の種類

力は大きく分けると非接触力、接触力にわけられます。そして非接触力は重力、クーロン力、磁場から受ける力の主に３つととても限られています。

物体に働く力を図示するときは、まず非接触力が働いていないかをみつけ、その力の大きさと向きを矢印で書き込みます。次に、物体と接触している場所はすべて物体に力を及ぼします。それらの力を矢印で表せばいいのです。

よくでてくる力は、

・重力→地球上の物体すべてに働き、向きは地球の中心に向かっています。

・弾性力→バネによる力でバネが伸びたり、縮んだりすると元の状態に戻ろうとするので、その方向に力が物体に働きます。

・抗力→ある物体Aが地面など他の物体に対して力が働くと、同じ大きさの力が反対向きに物体Aに対しても働きます。この力のことを指します。

・摩擦力→物体が摩擦のある面を移動するときに、摩擦力が生じます。摩擦力は垂直抗力に比例します。

・張力→例えば糸におもりをつけると糸がピーンと張ります。これが張力です。

などがあります。特徴をつかんでおくといいでしょう。

【物理】相対運動

2016.12.07

相対速度相対速度とはAからみたBの速度です。つまり、Aに自分を置いてみて、Bがどのような速度で運動しているかという値です。つまり、（Bの速度）ー（Aの速度）＝（相手の速度）ー（自分の速度）　で表されます。ここで２つの物体が一直線上にある場合は単純な引き算ですが、速

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]車にのりながら電車を見るといつもよりゆっくりに見えるよね。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]そうね。そうやって見える速さのことを相対速度っていうらしいよ。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]そうなんだ！[/speech_bubble]

相対速度

相対速度とはAからみたBの速度です。つまり、Aに自分を置いてみて、Bがどのような速度で運動しているかという値です。

つまり、（Bの速度）ー（Aの速度）

＝（相手の速度）ー（自分の速度）　で表されます。

ここで２つの物体が一直線上にある場合は単純な引き算ですが、速度は向きを含むベクトルなので一直線上にないときは注意しないといけません。

例えば、２つの物体が互いに垂直な向きに離れていく運動をしているとします。このときは相対速度の大きさは三平方の定理によってもとめ、向きはAの終点を始点、Bの終点を終点とするような矢印で表されます。

同様にして相対加速度も（相手の加速度）ー（自分の加速度）でもとめることができます。

相対運動の身近な例としては、電車に乗っているときに自分が乗っている電車と同じ方向に進んでいる電車を窓から見るとゆっくり見えたり止まっているように見える時があります。一方自分と逆向きに動いている電車を見るとものすごく速く見えます。またサッカーや野球の場合ボールと選手の動きが相対運動になるため、競技に慣れるまでなかなかボールが取れないのはこのためです。

例題）20m/sで運動している電車から、同じ方向に50m/sで運動している電車の相対速度vと逆向きに運動している電車の相対速度Vは？

v =（相手の速度）ー（自分の速度）＝５０ー２０＝３０m/s

V =（相手の速度）ー（自分の速度）＝５０ー（ー２０）＝７０m/s

【物理】放物運動(落体運動その2)

2016.12.07

放物運動とは、斜め方向に初速度を与えた運動です。この運動ではx方向、y方向について分けて考えるので、複雑のように感じますが、実際２つの運動は等加速度運動、等速度運動と意外と単純です。放物運動放物運動（斜方投射）は、いわゆる物を投げたときの運動を表します。ここでのポイントは運動をx

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]次は放物運動で式にcosθとかでてきちゃったよー！[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]しかも１つの運動なのにx方向とy方向に分けて考えるとかもう分からない…。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]なんでこうやって考えるんだろう。[/speech_bubble]

放物運動とは、斜め方向に初速度を与えた運動です。この運動ではx方向、y方向について分けて考えるので、複雑のように感じますが、実際２つの運動は等加速度運動、等速度運動と意外と単純です。

放物運動

放物運動（斜方投射）は、いわゆる物を投げたときの運動を表します。

ここでのポイントは運動をx方向は等速度運動、ｙ方向は等加速度運動と分けて考えることです。

今回地面からθの角度で、大きさ $v_{0}$ の初速度を与えたとします。（空気抵抗は無視します）

そのとき、x方向は進行方向を正とし、初速度は $v_{0}\cos \theta$ で表されます。また、力ははたらいていないので加速度a=０となります。

y方向では上向きを正とすると初速度は $v_{0}\sin \theta$ で表され、加速度ａ=-gとなります。

これらを等加速度運動の公式に代入することで、最高点や、落下までの時間、位置などを求める事ができます。今回の場合は各方向について以下のことがわかります。

・水平方向（x軸方向）： $v_{x}=v_{0} \cos \theta$ ・・・①、 $x=(v_{0}\cos \theta )t$ ・・・②

・鉛直方向（y軸方向）： $v_{y}=v_{0} \sin \theta -gt$ ・・・③、 $y=(v_{0} \sin \theta )t-\frac {1}{2}gt^{2}$ ・・・④

②、④を使って時間ｔを消去すると

$y=-\frac{g}{2v_{0}^{2} \cos^{2} \theta}x^{2}+(\tan \theta)x=-\frac{g}{2v_{0}^{2} \cos^{2} \theta} (x- \frac {v_{0}^{2} \sin 2\theta}{2g})^{2}+\frac {v_{0}^{2} \sin^{2}\theta}{2g}$ ・・・⑤

となり、ｙとｘは二次関数の関係になっています。この運動が放物運動と呼ばれる所以です。

ところで最高点では鉛直方向の速度成分はゼロになるので③において $v_{y}=0$ としてその時の時間を $t_{0}$ とすると

$t_{0}=\frac {v_{0}\sin \theta}{g}$

となります。このことから投げてから再び地面に着く時間は二次関数の対称性から投げてから $2t_{0}=\frac {2v_{0}\sin \theta}{g}$

となります。また⑤の $-\frac{g}{2v_{0}^{2} \cos^{2} \theta} (x- \frac {v_{0}^{2} \sin 2\theta}{2g})^{2}$ のところからθ＝45°のときが最もｘが大きい（最も飛ぶ）こともわかります。これは皆さんの実体験と合っているのではないでしょうか？

【物理】自由落下運動(落体運動その1)

2016.12.07

等加速度直線運動の1つの代表例が自由落下になります。基本中の基本なのでしっかり理解しましょう。自由落下自由落下とは、ある物体を初速度を与えずに、そっと落とした運動のことです。このときに働くのは下向きの重力で、加速度はg(≒9.8m/s2)で表されます。このときに注意しないと行けな

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]最近自由落下運動を習ったんだー！[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]あれ、難しいよね、なんで加速度が負になったり正になったりするんだ？[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]あれ？確かになんでだろう。そういうものだと思って暗記していたよ。[/speech_bubble]

等加速度直線運動の1つの代表例が自由落下になります。基本中の基本なのでしっかり理解しましょう。

自由落下

自由落下とは、ある物体を初速度を与えずに、そっと落とした運動のことです。このときに働くのは下向きの重力で、加速度はg(≒9.8m/s²)で表されます。

このときに注意しないと行けないのは座標の取り方です。最初の物体の位置を原点とします。そして、多くの場合では下向きを正とするので、下向きに働く加速度はgとなります。そのため、等加速度運動について成り立つ式は、a=g、v₀=0を代入することができ、

・v＝gt

・ $y=\frac{1}{2}gt^{2}$

・ $v^{2}=2gy　 \Longrightarrow v = \sqrt{2gy}$ 　　となります。

反対に、上向きを正にとり、加速度を−gとしても問題はありません。

鉛直投げ下ろし

鉛直投げ下ろし運動は自由落下に対して、物体に下向きの初速度を加えた運動です。このとき、まっすぐに投げ上げるので、ｙ方向についてのみ考えれば大丈夫です。

鉛直投げ上げ

鉛直投げ上げ運動は物体に上向きの初速度を与えた自由落下運動です。このとき、物体は上に運動した後、自由落下運動をします。

この場合は上向きを正に取り、加速度を−gとすることが多いので注意しましょう。

ここでポイントとなるのは、物体が最高点に達したときには速度が０であるということ、最高点に達するまでの時間と頂点から原点に戻るまでの時間は等しいということです。

例題）ボールを速さ19.6m/sで鉛直方向に投げ上げた。ボールが最高点に達するのは何秒後か。また、その高さは何ｍか求めよ。

公式に代入して、最高点ではv=0より、

最高点に達するまでの時間は

0＝19.6-9.8tより、t=2s

また、この時の高さは、

y=19.6t-1/2×9.8t^２=19.6×2-1/2×9.8×4=19.6m/s　　となります。

【物理】等速度運動、等加速度運動の３つの公式(変位、速度、加速度とは？その3)

2016.12.07

等速度運動、等加速度運動は高校物理でよくでてくる運動です。特に等加速度運動については速度、加速度、変位についての関係を示す３つの公式があるのでしっかり理解し、覚えてしまいましょう。等速度運動等速度運動とは、速度が一定である運動のことです。動いている物体に対して力が加わっていない

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]最近習った等速度運動とか、等加速度運動とか全然理解できない…。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]そうね、何が違うのかさっぱり分からない。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]同じ速度の運動と、同じ加速度の運動ってことかな？[/speech_bubble]

等速度運動、等加速度運動は高校物理でよくでてくる運動です。

特に等加速度運動については速度、加速度、変位についての関係を示す３つの公式があるのでしっかり理解し、覚えてしまいましょう。

等速度運動

等速度運動とは、速度が一定である運動のことです。

動いている物体に対して力が加わっていない場合、速度は変化しないので等速度運動になります。

等加速度運動

等加速度運動とは加速度、つまり速度の変化が一定である運動のことです。

高校物理ででてくる落下運動、摩擦の働く運動、など多くの運動は等加速度運動です。

また、以下の３つの公式が成り立ちます。

等加速度運動の３つの公式

この３つの公式は

・v＝v₀＋at

・ $x=v_{0}t+ \frac{1}{2}at^{2}$

・v^2_ーv₀²=2ax　　　の３つです。

ここでv₀は初速度です。

この３つの式は今後使う回数が非常に多いのですぐに覚えて、使いこなせるようになりましょう！

どの値がすでに与えられているのか、どの値を求めたいのかでうまく３つの公式を使い分けましょう。

例題）t＝0において3.0 m/sで運動している物体に進行方向と同じ向きに加速度2.0m/s²を与えた。t＝7 sのときの速度と変位を求めよ。

v＝v₀＋atにおいて、v₀＝3.0、a=2.0、t＝7より、

v＝3.0＋2.0×7＝17(m/s)

次に、 $x=v_{0}t+\frac{1}{2}at^{2}$ より、

x＝3.0×7+1/2×2.0×7^２＝70(m/s)

となります。

【物理】ベクトルとスカラーの違いは？(変位、速度、加速度とは？その1)

2016.12.07

力学で一番最初になるところですがここからわからなくなってしまう人も多いところです。物理ができるようになるコツは一つ一つ確実に理解していくことです。まず変位などの話に入る前にベクトルとスカラーの話からしていきます。スカラー量とベクトル量の違い日常会話でよく“速さ”と“速度”は同じ意味として使わ

…続きを読む
力学で一番最初になるところですがここからわからなくなってしまう人も多いところです。
物理ができるようになるコツは一つ一つ確実に理解していくことです。

まず変位などの話に入る前にベクトルとスカラーの話からしていきます。

スカラー量とベクトル量の違い

日常会話でよく“速さ”と“速度”は同じ意味として使われますが、物理学においては意味が違います。物理では

・速さはスカラー量

・速度はベクトル量　というものです。
[word_balloon id="1" position="L" size="M" balloon="line" name_position="under_avatar" radius="radius_12" avatar_border="false" avatar_shadow="false" balloon_shadow="true" font_color="#ffffff" bg_color="#70a6ff" font_size="22" balloon_full_width="true"]とはいえ、よくわからないと思うので、まずは言葉の違いから見ていきましょう。[/word_balloon]
スカラー量とベクトル量の言葉の違い

■スカラー量：大きさのみを持つ量

例：質量、面積、長さ、温度etc…

■ベクトル量：大きさと向きを持つ量

例：力、運動量、速度、加速度 etc…
[word_balloon id="3" position="R" size="M" balloon="line" name_position="under_avatar" radius="radius_12" avatar_border="false" avatar_shadow="false" balloon_shadow="true" font_color="#ffffff" bg_color="#70a6ff" font_size="22" balloon_full_width="true"]スカラーは普段使っている数字に近くて良いけど、ベクトルがわかりづらいな・・[/word_balloon]
物理で速度という場合“西“に”10ｍ/ｓ”というように必ず向きと大きさをセットでいわれます。
ベクトル量の場合数字のように単純な足し算が成立はしなくて、向きまで考慮しなければなりません。
そのためこの分野が苦手な人は二つの量をごちゃまぜにして考えているのが原因の一つにあると考えられます。

ベクトルとスカラーの問題例

①4 Nで引っ張ていた物体に、3 N さらに加えた。合計何N？

②右向きに4 Nで引っ張っていた物体に、右向きに3 Nをさらに加えた。合計何N？

③右向きに4 Nで引っ張っていた物体に、左向きに3 Nをさらに加えた。合計何N？

④東向きに4 Nで引っ張っていた物体に、北向きに3 Nをさらに加えた。合計何N？

①の文章を読んでこの分野が苦手な人は無意識に4+3＝7 [N]と考えてはいなかったでしょうか？
②ですとそれで正しいですが、③であると4－3＝1 [N]になります。④ですと三平方の定理から5 [N]になります。

特に上の文章の赤線部の影響が④は顕著に表れているのがわかると思います。

そのため物理で計算するときにスカラーかベクトルかをはっきりさせながら計算しないと間違えてしまうので注意しましょう

一つ注意したいのは、数直線上で考える場合だとスカラー量とベクトル量があいまいになることです。

たとえば、子供にりんごを1個ずつ配って、余ったら+5個で、足りなかったら-5個、と考えればこれもベクトルになります。

学校で習う最初の方は、一直線上の運動を取り扱うのでスカラーとベクトルをそこまで意識しなくても問題としては解けてしまうことが多いので、普段から意識して注意しましょう。

ベクトルとスカラーのまとめ

ベクトルとスカラーの違いの理解はできましたか。
学校ではこのような基本的な言葉の定義はなかな教えてくれない部分でもありますので、、
その他にも記事がありますので、読んでみてください。

v-tグラフとその意味とは？
等速度運動、等加速度運動の３つの公式
 定滑車、動滑車

また、当塾では、今回のような基本的な定義の部分からどのように理解をしたら良いのかを0からお伝えしております。
このような基本的なレベルを0から理解していくことは早慶合格への重要なステップとなります。

具体的に0から早慶に合格するために何をしたら良いのかのご相談はこちらから行なっております。

【数学】不等式とは？これを知らないと数学人生が大きく変わる!

2016.12.04

不等式とは左辺と右辺の大小関係を示している式です。不等式で使われる記号は５つあります。このような記号を不等号といいます。ｘ＞ｙ：ｘがｙより大きいｘ＜ｙ：ｙがｘより大きいｘ≧ｙ：ｘがｙ以上（ｘがｙより大きい、又はｘとｙは等しい）ｘ≦ｙ：ｙがｘ以上ｘ＝ｙ：ｘとｙが等しい 5つあるといっても、

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]等式はわかるんだけど、不等式ってその反対って意味？[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]左辺と右辺、どっちが大きいとか小さいとかそういうやつよ。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]あーなるほど！以上とか未満とかよくわからないなー[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]確かに、不等式って等式よりもなんだか難しい。。[/speech_bubble]
不等式とは左辺と右辺の大小関係を示している式です。
不等式で使われる記号は５つあります。このような記号を不等号といいます。

ｘ＞ｙ：ｘがｙより大きい

ｘ＜ｙ：ｙがｘより大きい

ｘ≧ｙ：ｘがｙ以上（ｘがｙより大きい、又はｘとｙは等しい）

ｘ≦ｙ：ｙがｘ以上

ｘ＝ｙ：ｘとｙが等しい

5つあるといっても、不等号の口の開いている向きが反対なだけで、覚えることは全然ありませんね。
口の開いている方が大きい値、イコールが入ってるか入ってないかに気をつける。
これだけ意識しておけば問題ありません！

解くのもほぼ等式と同じように行うことができます。

”ほぼ”というように違うところもあるのでちゃんと読んでくださいね！

不等式の解き方

不等式も等式と同じように展開、移項、かけ算割り算を繰り返すことで
未知の文字について解くことができます。

注意が必要なのが不等式は等式と違って、負の数を両辺にかけたり割ったりする場合には不等号の向きを反転させる必要があるってことです。

これ、重要でしかも忘れちゃう人が非常に多いので頭に叩き込んでくださいね！

これはなぜかと言うと、
イメージ的には、負の数は数字自体が大きければ大きいほど値としては小さくなっていくというところと関係があります。
例えば、-2と-5という数字は数字が大きれば大きいほど小さくなりますね。
これはプラスの場合が大きい数字であればあるほど数が大きくなるプラスの場合とは、逆の関係ですね。

→上記のように、学校ではただルールとして教わっていることのなぜ？を考えることが数学や理科系の成績を上昇させるためのポイントです。
積極的になぜを考えるようにしていきましょう。

もうひとつ注意する点としては、不等号の種類や向きを勝手に変えないことです。

こちらも実際にやってみないと実感がわかないと思いますのでやってみます。

不等式の例題

問題：２ｘ＋８＞３ｘー３

答え：２ｘ−３ｘ＞−３−８　　　　←左側をｘだけにする

ーｘ＞−１１　　　　　　　　　　←ｘにマイナスがついてる！！

ｘ＜１１　　　　　　　　　　　　←不等号の向きを逆にする！

答えはｘ＜１１です。

不等号の向きを逆にするとはこういうことです。
マイナスをかける瞬間に一緒に逆にしなきゃってことです。

ちなみに移項をする操作では、マイナスがついてても不等号の向きを逆転させる必要はありませんよ。
これも間違う人が多いので注意です

基本の操作は方程式、連立方程式と同じです。そろそろ慣れてきましたか？

気をつけるのは不等号を逆転させる所だけですから、早めにマスターしてしまいましょう！

不等式は数学の基本ですが、不等式と同じくらい重要な概念に方程式もあります。方程式についてはこちらの記事をどうぞ！

[nlink url="https://hiroacademia.jpn.com/blog/5minutes/5minmt/hoteishiki/"]

【数学】連立方程式とは？| 5分でわかる受験のキソノキソ

2016.11.30

このように連立方程式を苦手としている人は多いのではないでしょうか。そもそも連立方程式とは、何本かの方程式がセットになって全部成り立っているやつのことで、方程式の本数分だけ、未知数（xとかyとか）の値を求める事ができます。つまり、方程式2本なら文字2つ（x、y）方程式が3本なら文字3つ（x、y、

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]連立方程式、いまいちどうしたら楽に解けるのかわからない…[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]連立方程式ってどんなのだっけ？[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]ほら、二本の方程式があるやつだよ[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]あれかあ…。どっちの式を何倍とかややこしいわよね(ToT)[/speech_bubble]
このように連立方程式を苦手としている人は多いのではないでしょうか。

そもそも連立方程式とは、何本かの方程式がセットになって全部成り立っているやつのことで、方程式の本数分だけ、未知数（xとかyとか）の値を求める事ができます。

つまり、方程式2本なら文字2つ（x、y）
方程式が3本なら文字3つ（x、y、z）まで求まるんです。

ここでは連立方程式として最もよく出題される「二元連立一次方程式」（2つの文字を含む連立された一次の方程式）の解き方をやっていきたいと思います！

連立方程式の解き方

連立方程式を解くには、主に2つの方法があります。

まず、代入法と呼ばれる方法です。
片方の式をx= や y= の形に変えて、それをもう片方の式に代入することで文字を１つ減らし、答えをもとめる方法です。

もう一つは加減法と呼ばれる方法です。
まず、式を何倍かすることで１つの文字について係数を合わせます。そこから、２つの式を足し引きすることでその文字を消去し、答えを求める方法です。

両方とも同じ答えがでるのでどちらで解いてもいいですが、
両方使えるようになってより早い方法を選べるようになっておくのが理想です！

では例題を見てみましょう。

連立方程式の例題

問題：ｘ＋ｙ＝３　ー（１）

２ｘ＋５ｙ＝９　ー（２）　　の連立方程式を解け。

答え：代入法で行う場合

ｘ＋ｙ＝３　を、ｘ＝ーｙ＋３に変形します。

これをもう片方の式に代入して、　２（ーｙ＋３）＋５ｙ＝９　　　←普通の1次方程式！

これを解くと、ｙ＝１

ｘ＝ーｙ＋３より、ｙの値を代入してｘ＝２

加減法で行う場合

ｘの係数を合わせることにします。
（１）式を２倍して、２ｘ＋２ｙ＝６

（２）ー（１）を行うと、３ｙ＝３　よってｙ＝１

（１）にこの結果を代入すると、ｘ＝２

以上が2つの解き方です。
当然ですが同じ答えにちゃんとなってますね！

この問題なら代入法と加減法、どちらのほうが良いと思いましたか？

この問題の場合、どちらでやっても手間はほとんど変わりません。
しかし、問題によっては代入法で解くのが面倒になってしまうものもあります。
例）連立方程式
3x+5y=13
2x-3y=-4　　　　　　を解け。

これを代入法、加減法でそれぞれ解いてみてください。
加減法が面倒な場合も多い、ということがわかると思います。

もし分からなかったら、あなたはこれから代入法愛用者になっても構いません☆
自分の好きな方法で解きましょう！

【数学】定数と変数の違いに答えます！

2016.11.29

などとよくわからない認識をしている人はいませんか？あるいは分からなくても問題ないし〜と思っていませんか？数学を得意としてる人でも、いざ違いはと聞かれると答えられない人も多いのではないでしょうか。定数と変数の意味の違い、それが分かると分からないでは数学の理解にも差が出てきます！今この機会にそれを

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]数学の教科書とかでさあ、定数とか変数とかあるじゃん。あれってどういう意味？[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]定まってる数と変わる数のことよ。そのままよ。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]それがわからないから聞いてるんじゃん！[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]うーんそうねえ。xとかyとかは変わりそう。きっと変数よ。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]じゃあ1とか2とかいう数字が定数ってことかな。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]あれ、でも定数aを求めよって問題もあるわよね…aとかbとかは定数なのかも！[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]なるほど文字の種類によって定数か変数かが違うんだね！ありがとう山田さん！[/speech_bubble]

などとよくわからない認識をしている人はいませんか？

あるいは分からなくても問題ないし〜と思っていませんか？

数学を得意としてる人でも、いざ違いはと聞かれると答えられない人も多いのではないでしょうか。定数と変数の意味の違い、それが分かると分からないでは数学の理解にも差が出てきます！
今この機会にそれを学んでおきましょう。

定数、変数違いとは？

難しそうな言葉が出てきたもうやだつらいやめよう。。。。

なんて言わないでください。難しく考える必要はありません。

定数とは「値が変化しないもの。定まっているもの。」
変数とは「値が変化するもの。定まっていないもの。」

意味としては漢字のそのまんまです。ただそれだけです。
でもこれだけ言われてもだから何？状態ですね。
もう少し詳しく見ていきましょう。

定数の意味とは

まず小山くんが「1とか2とかいう数字は定数かなあ」と言っていましたが、それは正しいでしょうか？　正しくないでしょうか？

これは正しいです。1、2と値が定まっているのですから定数となりますね。
これは知っていまえば誰でも見分けがつきます。簡単です。

問題は文字の定数です。
「文字ってことは何の値が入るかわからないんでしょう。そんなのxとかyと何が違うんだよ〜〜」
そのお気持ち大変よく理解できます。何が違うのでしょう？

ここでひとつ確認しておきたいことは「値が分からない」ことと「値が定まっていない」ことは別問題であるということです。

つまり、問題でよく出てくる「定数aの値を求めよ。」というとき、aの値はまだ我々にはわからないけれども、実は何かしらに定まった値を持っている！ということなのです。

問題たちは、その実は定まってる値をあなたたちで見つけてくれよって言ってるわけですね！

変数の意味とは

ではそれに対して変数とは一体何だったのでしょう。

変数とは、いろいろな値を取れる数です。
xやyで表されることが一般的なのではないでしょうか。

関数を考えてみると、より分かりやすくなります。

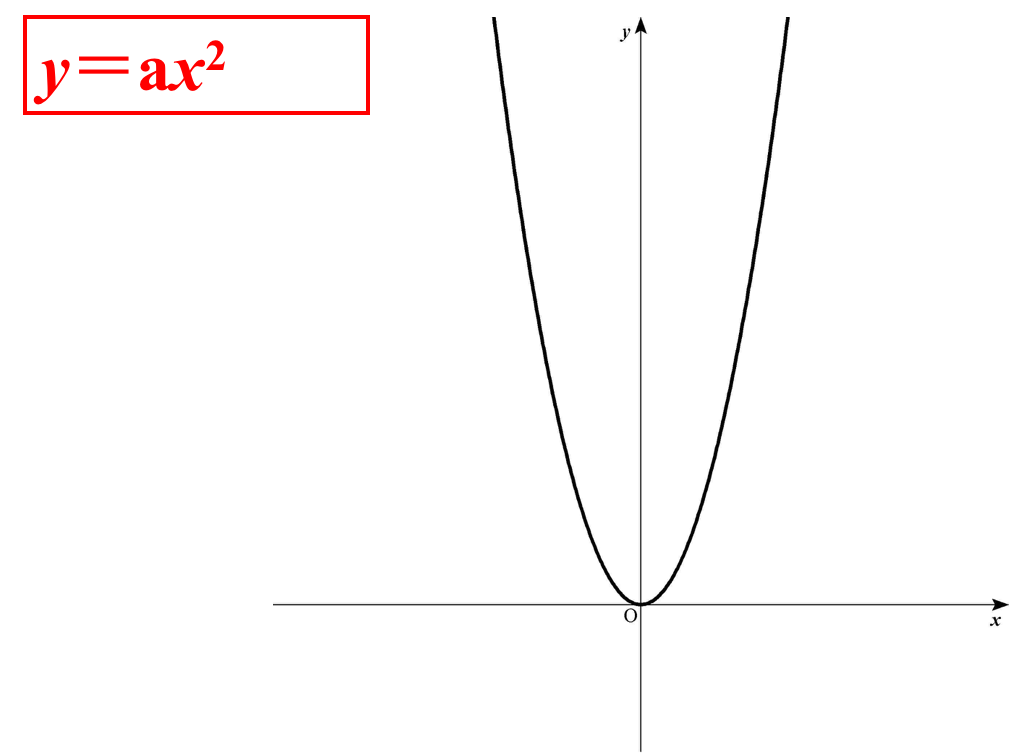
例えばy=ax²という関数を考えてみます。xとyが変数でaを定数と見ます。

グラフを考えれば分かるように、xはいろいろな値を取ることができますし、それにともなってyもいろいろな値を取りますね。
つまり「定まっていない値」「変化する値」になっています。
一方aは、たとえば1だったり、−2だったり、ある一定の値を取る文字です。

例題

今まで日本語で説明してきましたが、ここで簡単な例題を考えて終わりにしましょう。

問題：y=ax² (xとyが変数でaが定数) が(x,y)=(2,-8)を通るとき、定数aの値を求めよ。

解答：y=ax² に (x,y)=(2,-8) を代入して -8=4a ∴a=-2

とても初歩的な問題ですが、この問題を噛み砕いてみます。

xとyはいろいろな値を変化する値ですが、その(x,y)=(2,-8)という座標は通っています。

ところでaは、実は定まった値を取るらしいのですがそれがまだ分からないので、それを求めましょうね。　ということです！

上記ではy=の形を使って定数変数をの説明をしていますが、そもそも方程式の意味がわからない場合はこちらをどうぞ！
[nlink url="https://hiroacademia.jpn.com/blog/5minutes/5minmt/hoteishiki/"]

少しつかめましたか？
今後「定数」「変数」という言葉を見かけたら少し立ち止まって考えてみてください。　
理解が深まると思います。

上記のような理解をしていくことで数学の成績も着実に上げることができます。今後具体的に成績を上げるための数学の勉強法はこちらにあります。
[nlink url="https://hiroacademia.jpn.com/blog/program/saisokumarth-schedule/"]

定数変数まとめ

定数と変数についての理解はできましたか。
学校ではこのような基本的な言葉の定義はなかな教えてくれない部分でもありますので、、
今回の記事で理解ができたのであれば幸いです。

また、当塾では、今回のような基本的な定義の部分からどのように理解をしたら良いのかを0からお伝えしております。
このような基本的なレベルを0から理解していくことは早慶合格への重要なステップとなります。

統帥権とは？

2016.11.16

統帥権とは？統帥権とは、一言で言うと「軍隊を運用する権力」のことです（◯帥　✕師）。この「軍隊を運用する権力」には、軍隊を動かして戦争を行うことはもちろん、軍備を用意するなどと言ったことも含まれます。統帥権は軍隊（またはそれに準ずる戦力）があれば、必ず存在するもので、その用いられ方のパターンは

…続きを読む
統帥権とは？

統帥権とは、一言で言うと「軍隊を運用する権力」のことです（◯帥　✕師）。
この「軍隊を運用する権力」には、軍隊を動かして戦争を行うことはもちろん、軍備を用意するなどと言ったことも含まれます。
統帥権は軍隊（またはそれに準ずる戦力）があれば、必ず存在するもので、その用いられ方のパターンは２つあります。

まず1つ目に、
統帥権は軍部が持っていて、内閣と独立しているパターンがあります。
これは明治時代に主に用いられていた方法で、ここでは、内閣が軍部を無視して勝手に条約を結んで軍隊を縮小したり、戦争をやめたりすることは許されません。
それは、軍隊に関することの決定権はこの場合、軍部が持っているからです。

2つ目の用いられ方は、
統帥権は軍部ではなく、文民の内閣総理大臣が持っているパターンです。
これは現在の用いられ方で、ここでは現場の人たちが勝手に軍隊を動かして攻撃を仕掛けることは許されません。
それは軍隊の運用に関する決定権はこの場合、内閣が持っているからです。

以上のように、統帥権は明治時代以降の歴史を学ぶ上で非常に重要な用語になります。
「統帥権とは何なのか？」「統帥権は軍部が持っているのか、内閣が持っているのか」などをしっかり理解した上で、学習を進めてもらいたいと思います。

1 ‹ Previous … 6 7 8 9 10 11

力

力の種類

相対速度

放物運動

自由落下

鉛直投げ下ろし

鉛直投げ上げ

等速度運動

等加速度運動

等加速度運動の３つの公式

スカラー量とベクトル量の違い

スカラー量とベクトル量の言葉の違い

ベクトルとスカラーの問題例

ベクトルとスカラーのまとめ

不等式の解き方

不等式の例題

連立方程式の解き方

連立方程式の例題

定数、変数違いとは？

定数の意味とは

変数の意味とは

例題

定数変数まとめ

統帥権とは？