入試難易度: 4.0
4.0
全体概観:配点100点 時間60分
大問3問構成のことが多く、小問数は約70。解答形式は選択式・記述式と論述式です。
時間的には問題ないと思いますが、あまりゆっくりしていると足りなくなる可能性もあります。
問われている用語自体はほとんど教科書レベルからの出題で、かつ、スタンダードな問題が出題されます。
教科書や参考書で「これが重要」というものを素直に覚えていきましょう。
ただし、一部非常に難易度の高い問題も出題されています。
そのような問題は必ずできなければならない問題ではありません。
恐らく正誤判定問題は差がつくところなので気を付けてください。
記述問題もたくさんあるので、漢字で書けるようにすることも大切です。
中国史に限らず、用語は漢字で書けるようにしてください。
意外と中国史以外のところで漢字で書けず失点することがあります。漢字は普段から意識して勉強してください。
分野別では政治史、社会経済史、文化史などどの分野からもまんべんなく出題されています。
もちろん、法学部ですから法律や条約などはよく出題されますが、そればかりが出題されるというわけでもありません。
時代的にも古代から近現代までまんべんなく出題されます。
地域的にもまんべんなく出題されています。西洋では西ヨーロッパを中心にロシアやアメリカも出題されていますし、東洋では中国やイスラームを中心に小問で東南アジア等に触れています。
また、テーマ史も出題されています。「博物館」をテーマにした大問が出題されたこともあります。このような問題ではあらゆる時代・あらゆる地域について問われますが一問一問は特別な難問というわけでもないので冷静に一問ずつ解いていけば対処できると思います。
対策1: 論述はどのように対策をしていけばよいのか?
通常の勉強をしているだけではなかなか論述問題はできるようにはなりません。
特に、私大だと一問一答でアウトプットを済ましてしまう場合が多いのですが、それではいつまでたっても論述問題はできるようにはならないのです。
論述問題は、歴史上の複数の事項を論理的に捉えていかなくてはいけません。論理的というのはこの場合因果関係と相関関係を意味します。
何が原因で何が発生したのか?、またそれと同時期におこっていた事件との関連はどのようにあるのか?、などです。歴史項目と歴史項目を図式化して→で論理の関係を考えてみてください。
対策2:正誤問題はどのように対策をしていけばよいのか?
まず正誤問題はとても難しいということを認識しましょう。
非常に判定しづらい問題があるのも事実です。また、本当に正確に解くには正確な知識が4つも必要です。空欄補充なら1つでも大丈夫なのに…。
普段から正答でない選択肢についてもよく復習し、「なぜこの解答なのか」「なぜこれは誤答なのか」を言えるようにしていってください。
どんな細かい点でも正確な知識を追及していくことが大切です。
正答にならない選択肢もよく確認するようにしましょう。そのなかで知識の確認もできます。
これを繰り返していくことで力が付き、正誤判定問題を解くこともできるようになっていきます。
当たり前のことをできるようになった人が合格します。
大学受験では100点を取ることではなく、人より1点多くとることが大切です。
また、1位じゃなくても大丈夫です。
100人合格するならば、100位に入ればいいのです。
そう考えた時に、中央大学の世界史で合格点を取るには教科書レベルの知識事項で点数を落とさないこと、難問に関しては(できるに越したことはありませんが)できなくてもくよくよせずに次の問題に進むことが大切になります。
中央大学法学部に合格するための参考書
当塾で使用している中央大学法学部に合格へ必要な参考書を紹介します。もちろん、当塾の場合は一人一人個別にカリキュラムを作成するため下記のようなカリキュラムは一例となります。参考書は何をやるかよりも、どのような目的で使用するかというが大事です。闇雲に行って情報量に圧倒されてしまうのではなく、1つ1つ目的意識を持って勉強していきましょう。
参考書だけでの独学での合格はかなり難しく、初学者の場合は指導なしでやってしまうと下手な癖が付く可能性が高いです。下手な癖がつくと、その癖を治すのに手一杯で結局志望校に受からないというケースが多くなっています。浪人しても成功しない人はこの辺りに理由があります。
ご心配な方は一度カウンセリングを受けて見ると良いでしょう。カウンセリングはこちらからどうぞ。
■下記参考書名をクリックすると詳しい使い方のページに飛びます。
▶初歩(偏差値40程度)
とってもやさしい世界史
▶基礎(偏差値40~55程度)
パノラマ世界史
時代と流れで覚える世界史B用語
▶応用(偏差値55~65程度)
ナビゲーター世界史
ヒストリア世界史問題集(*時間のない場合は行う必要はなく過去問で問題を解くことで対策をしていくと良いでしょう。)
中央大学法学部に圧倒的な実力で合格できる専門対策をします
まずは資料請求・お問い合わせ・学習相談から!
HIRO ACADEMIAには、中央大学の徹底指導合格塾として法学部への圧倒的な合格ノウハウがございます。
少しでもご興味をお持ちいただいた方は、まずは合格に役立つノウハウや情報を、詰め込んだ資料をご請求ください。
また、中央大学法学部に合格するためにどのように勉強をしたらよいのか指示する学習カウンセリングも承っています。学習状況を伺った上で、残りの期間でどう受かるかを提案いたしますので、ぜひお気軽にお電話いただければと思います。
⇒中央大学法学部に合格したい方は、まずは当塾の資料をご請求ください。

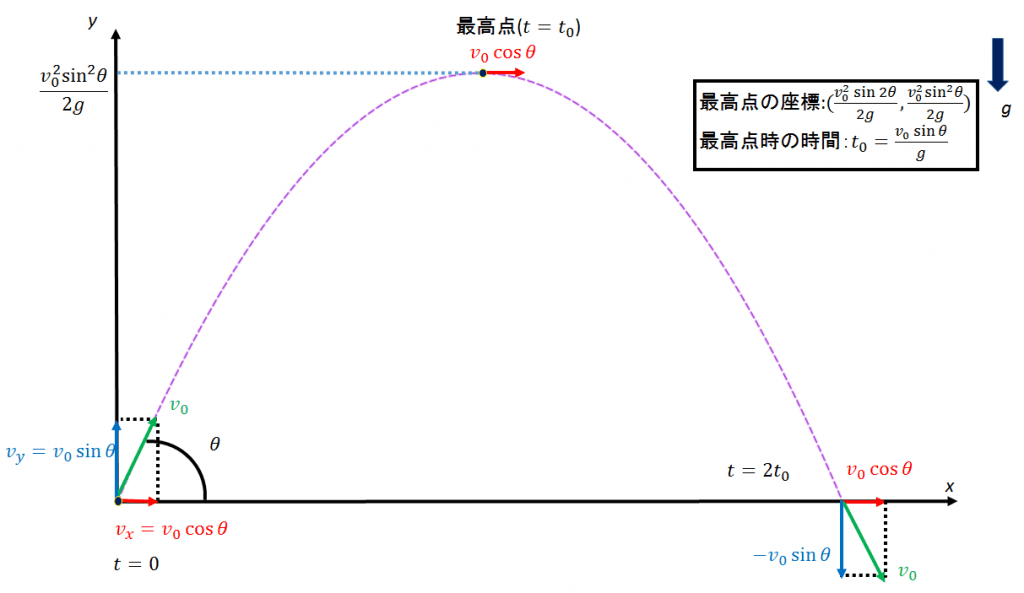
 の初速度を与えたとします。(空気抵抗は無視します)
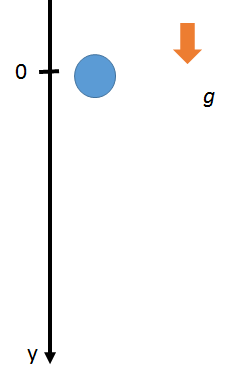
の初速度を与えたとします。(空気抵抗は無視します) で表されます。また、力ははたらいていないので加速度a=0となります。
で表されます。また、力ははたらいていないので加速度a=0となります。 で表され、加速度a=-gとなります。
で表され、加速度a=-gとなります。 ・・・①、
・・・①、 ・・・②
・・・② ・・・③、
・・・③、 ・・・④
・・・④ ・・・⑤
・・・⑤ としてその時の時間を
としてその時の時間を とすると
とすると

 のところからθ=45°のときが最もxが大きい(最も飛ぶ)こともわかります。これは皆さんの実体験と合っているのではないでしょうか?
のところからθ=45°のときが最もxが大きい(最も飛ぶ)こともわかります。これは皆さんの実体験と合っているのではないでしょうか?