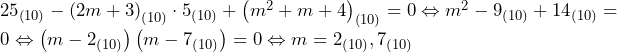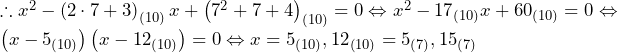方針の立て方 円が他の図形と接する場合には,中心と接点を結ぶと上手くいくことが多い.これは,中心と接点を結んだ線は接線と直交することによる. 甲円の直径は上記の方針で解ける. 上甲円の中心と直線との距離,および,丙円の直径については,長さ求める線分を実際に引いてみると題意をつかみやすい.線分を引くと
- …続きを読む
- 方針の立て方
円が他の図形と接する場合には,中心と接点を結ぶと上手くいくことが多い.これは,中心と接点を結んだ線は接線と直交することによる.
甲円の直径は上記の方針で解ける.
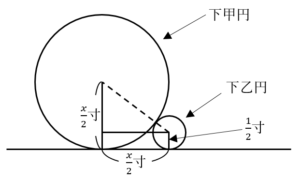
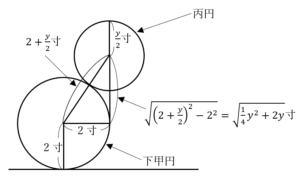
上甲円の中心と直線との距離,および,丙円の直径については,長さ求める線分を実際に引いてみると題意をつかみやすい.線分を引くと下甲円の接線となるので,下甲円の中心とその接点を結んでみると解法を得られるだろう.
また,図形の問題に限らず数学の問題では,同じものを2通りの形に表してそれらをイコールするという解法が多い(丙円の直径はまさしくこの解法)ので押さえておこう.解答例
(1)(2)……04
(3)(4)……02
(5)(6)……05
(7)(8)……16
(9)(10)……07
(11)(12)……05
(13)(14)……11
※(3)~(14)の解答は,上下の甲円の中心を結んだ線分が,それらの甲円に内接している乙円の中心を通ると仮定した際の解答解説
〇甲円の直径((1)と(2)について)

求める甲円の直径を 寸とおく.
寸とおく.
上図で中心間距離(図中の破線)について,三平方の定理より,

が成り立ち, のもとで,これを解くと,
のもとで,これを解くと, .
.
 4寸……(答)
4寸……(答)〇上甲円の中心と直線との距離((3)~(6)について)

上図より, 寸離れている……(答)
寸離れている……(答)〇丙円の直径
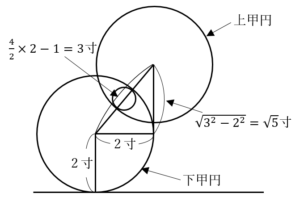
上甲円の最上部と直線との距離は,前問の結果を用いれば, 寸と分かる.
寸と分かる.
求める丙円の直径を 寸とする.
寸とする.

すると,左図より,上甲円の最上部と直線との距離は,
 寸
寸
とも表せる.

これを解くと,
 寸……(答)
寸……(答)









![Rendered by QuickLaTeX.com a_n=\int_{0}^{1}\left(1-x^2\right)^\frac{n}{2}dx=\int_{0}^{1}{\left(x\right)^\prime\left(1-x^2\right)^\frac{n}{2}}dx=\left[x\left(1-x^2\right)^\frac{n}{2}\right]_0^1-\int_{0}^{1}{x\cdot\frac{n}{2}\left(1-x^2\right)^\frac{n-2}{2}\cdot\left(-2x\right)}dx=n\int_{0}^{1}{x^2\left(1-x^2\right)^\frac{n-2}{2}}dx](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-3383a4e3a41de53f568ac6beddb7b89b_l3.png)
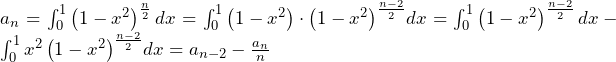
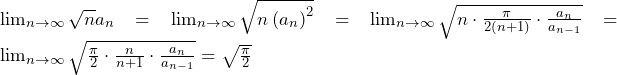 ……(答)
……(答)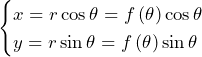
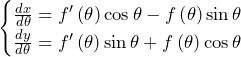
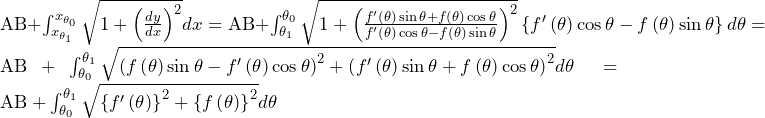
![Rendered by QuickLaTeX.com \mathrm{AB}+\int_{\theta_0}^{\theta_1}\sqrt{\left\{f^\prime\left(\theta\right)\right\}^2+\left\{f\left(\theta\right)\right\}^2}d\theta=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}\sqrt{\left\{\alpha\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2+\left\{\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2}d\theta\bigm=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}{\sqrt{1+\alpha^2}\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}}d\theta=\frac{v}{\sqrt{v^2-1}}+\sqrt{1+\alpha^2}\beta\left[\frac{1}{\alpha}e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right]_{\frac{\pi}{2}}^{\theta_1}\bigm=\frac{v}{\sqrt{v^2-1}}-\frac{\beta}{\alpha}\sqrt{1+\alpha^2}+\frac{\beta}{\alpha}\sqrt{1+\alpha^2}e^{\alpha\left(\theta_1-\frac{\pi}{2}\right)}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-3251c46fb035b1c6f3d900fd751c1cf5_l3.png)
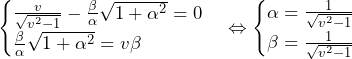 ……(答)
……(答)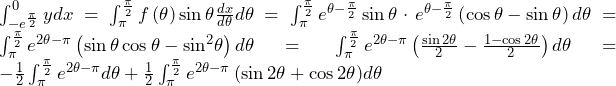
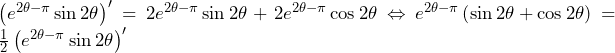
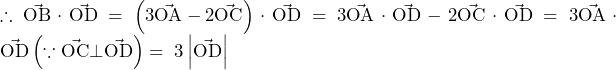 (
(

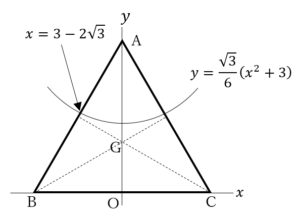
![Rendered by QuickLaTeX.com 2\int_{3-2\sqrt3}^{0}\left\{\left(\sqrt3x+\sqrt3\right)-\left(\frac{\sqrt3}{6}x^2+\frac{\sqrt3}{2}\right)\right\}dx=\left[-\frac{\sqrt3}{9}x^3+\sqrt3x^2+\sqrt3x\right]_{3-2\sqrt3}^0=16-9\sqrt3](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-ca7e2526c667d1ae7bb1ab5fab12914c_l3.png) ……(答)
……(答)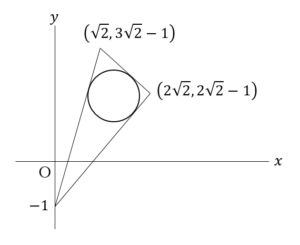
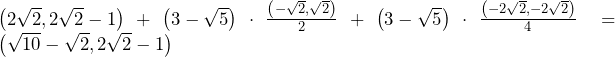 ……(答)
……(答)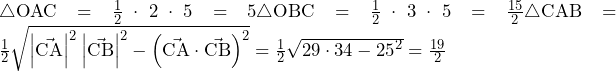 より,
より,