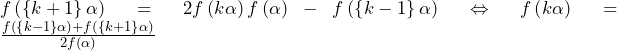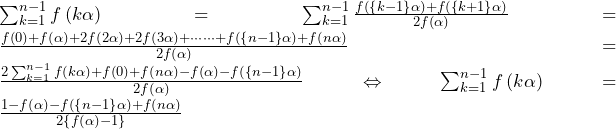方針の立て方 (1) 典型問題であるため特筆事項なし. (2) 前問と同様の解法を用いると考える. 前問では,中心座標が与えられていたためここから考えられたが,本問では中心座標が与えられていない.そこで,まずは中心を文字で置くことから始める.すると前問の解法の流れが使える. (3) まずは,半径の情
- …続きを読む
-
方針の立て方
(1)
典型問題であるため特筆事項なし.(2)
前問と同様の解法を用いると考える.
前問では,中心座標が与えられていたためここから考えられたが,本問では中心座標が与えられていない.そこで,まずは中心を文字で置くことから始める.すると前問の解法の流れが使える.(3)
まずは,半径の情報が与えられている円 の議論をする.(1)や(2)と同様に中心座標を文字で置いて議論すれば良い.
の議論をする.(1)や(2)と同様に中心座標を文字で置いて議論すれば良い.
解答に至るには円 の中心に関する議論が必要になるから,円
の中心に関する議論が必要になるから,円 と円
と円 の情報をつなげる(というより円
の情報をつなげる(というより円 の情報を円
の情報を円 の情報に変換する)ことを考える.本問では線分
の情報に変換する)ことを考える.本問では線分 の長さの情報が与えられているため,これを使ってやれば良い.直線
の長さの情報が与えられているため,これを使ってやれば良い.直線 の傾きが三角比でよく見る
の傾きが三角比でよく見る という値であることから,図形的に考えれば良いと直観する.
という値であることから,図形的に考えれば良いと直観する.解答例
(1)

(2)
(3)(4)
(5)
(6)
(7)(8)
(9)
解説
(1)
中心が であり,
であり, 軸と接することから,円
軸と接することから,円 の半径は1である.……(答)
の半径は1である.……(答)
また,円 は直線
は直線 と接することから,中心
と接することから,中心 と直線
と直線 との距離は半径の長さ1と等しくなる.
との距離は半径の長さ1と等しくなる.
 ……(答)
……(答)(2)
円の中心の座標を (
( は実数)とおく.すると,円
は実数)とおく.すると,円 の方程式は,
の方程式は,

まず, 軸と接することから,
軸と接することから, .
.
また,円 は直線
は直線 と接することから,中心
と接することから,中心 と直線
と直線 との距離は半径の長さ2と等しくなる.
との距離は半径の長さ2と等しくなる.

よって,円の中心は の4点.この4点からなる平行四辺形の面積が求める面積であり,
の4点.この4点からなる平行四辺形の面積が求める面積であり,
 ……(答)
……(答)(3)
円 の中心座標を
の中心座標を (
( は正の実数.また,
は正の実数.また, 座標が1となることは,半径が1であることと
座標が1となることは,半径が1であることと 軸に接することから明らか)とおく.
軸に接することから明らか)とおく.
すると,円 の方程式は,
の方程式は,

と書ける.これが直線 と接することから,中心
と接することから,中心 と直線
と直線 との距離は半径の長さ1と等しくなる.
との距離は半径の長さ1と等しくなる.

 は正の実数であることより,
は正の実数であることより, が適当.
が適当.
よって,円 の方程式は
の方程式は であり,直線
であり,直線 との接点
との接点 の座標を求めると
の座標を求めると と分かる.
と分かる.
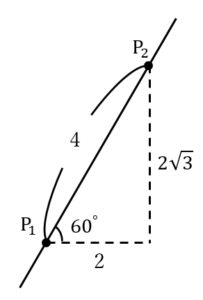
下図のように考えると, の座標は
の座標は と分かる.
と分かる.

円 の中心の座標を
の中心の座標を (
( はともに正の実数)とすると,
はともに正の実数)とすると, 軸と接することから円
軸と接することから円 の半径は
の半径は となる.
となる.
また,中心 は,点
は,点 を通る直線
を通る直線 の法線上にある.その法線の方程式は,
の法線上にある.その法線の方程式は, であるから,
であるから, となる.
となる.
更に,中心 と直線
と直線 との距離は半径
との距離は半径 と等しくなるから,
と等しくなるから,

 と連立し,更に
と連立し,更に が正の実数であることを用いれば,
が正の実数であることを用いれば,
 ……(答)
……(答)







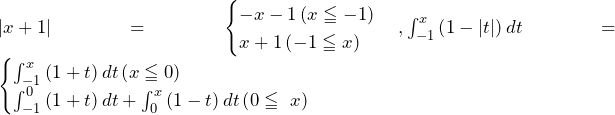 となる.
となる.![Rendered by QuickLaTeX.com F\left(x\right)=x+1+\int_{-1}^{0}\left(1+t\right)dt+\int_{0}^{x}\left(1-t\right)dt=x+1+\left[t+\frac{1}{2}t^2\right]_{-1}^0+\left[t-\frac{1}{2}t^2\right]_0^x=-\frac{1}{2}x^2+2x+\frac{3}{2}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-41c71a6f673b63fa745fc3d548c4ed52_l3.png)
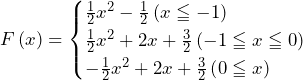 ……(答)
……(答)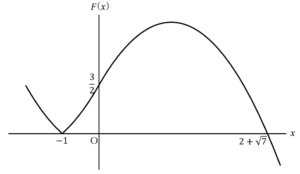
![Rendered by QuickLaTeX.com \int_{-1}^{0}\left(\frac{1}{2}x^2+2x+\frac{3}{2}\right)dx+\int_{0}^{2+\sqrt7}\left(-\frac{1}{2}x^2+2x+\frac{3}{2}\right)dx=\left[\frac{1}{6}x^3+x^2+\frac{3}{2}x\right]_{-1}^0+\left[-\frac{1}{6}x^3+x^2+\frac{3}{2}x\right]_0^{2+\sqrt7}=\frac{19+7\sqrt7}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-49c0c64db15f48db2771431bf99b4c3e_l3.png) ……(答)
……(答)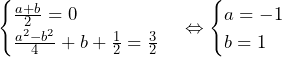
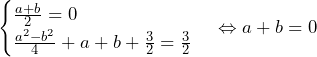
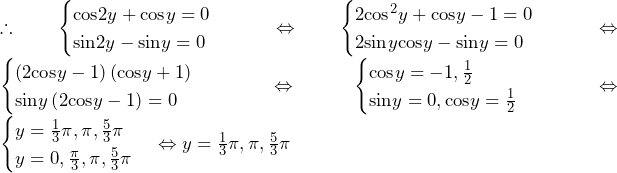 ……(答)
……(答)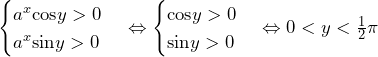
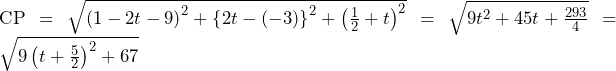
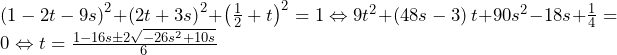
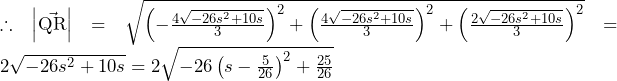
 ……(答)
……(答)