なんで私が東大に・・・というキャッチコピーで有名な四谷学院さんについてお伝えしていきます。55段階で生徒の学力を測ることができるという画期的な仕組みを提供している四谷学院さんですが、いかにして成績の低い生徒の成績をあげていくことができるかをお伝えできれば・・・と思います。 そのシステムとは &nbs
- …続きを読む
- なんで私が東大に・・・というキャッチコピーで有名な四谷学院さんについてお伝えしていきます。55段階で生徒の学力を測ることができるという画期的な仕組みを提供している四谷学院さんですが、いかにして成績の低い生徒の成績をあげていくことができるかをお伝えできれば・・・と思います。
[toc]
そのシステムとは
特徴 その1 55段階での生徒の学力の評価、科目別能力授業
科目別に生徒の学力を判定して、55段階でわけるというシステムを取っています。
そのため、苦手な科目は中学レベルで、得意な科目は国公立コースといった取り方も可能です。
中学生の基礎レベルから東大レベルの問題まで無駄なくステップアップできるようになっています。まだ、自分で気づくことのできないミスをプロ講師がその場で教えてくれるため効率よく成績を上げることができます。
特徴 その2 集団と個別のダブル授業
集団授業だけでなく、個別指導とのダブル授業が可能です。
基本は集団授業ですが、苦手な科目だけ個別で行う・・という取り方もできて、
効率的に成績を上げることが可能です。
特徴 その3 中学レベルからでも対応が可能
55段階という分け方はかなり細かく細分化されていると言えますね。
入塾した時期は中1レベルであっても、入試直前には東大合格のレベルにまで到達しているということはよくあることのようです。
このシステムをうまく使うことで最短で効率的に合格してくことができると言えるでしょう。
評判、口コミは?
四谷学院さんは55段階をうまく使えるかどうかがキーポイントになるでしょう。
そのため、入った時期によってはうまく使えこなせない生徒もいるため、不満の声が上がっているようです。料金は?
基本指導で年間 750,000〜800,000円ほどで、夏期、冬期講習で別途指導がありまた、別途個別も行った場合はもう少し値段がかかるようです。
こういった人におすすめ
上述しましたが、合格できるもできないも55段階をうまくこなすことができるかが、合否の分かれ目になってきます。
55段階の評価というのはかなり細分化されていますので、
大学入試までの期間に比較的時間のあるか、部活などをしていなくて時間のある生徒にはオススメの塾でしょう。四谷学院とHIRO ACADEMIAとの比較
四谷学院という素晴らしい塾がある中で恐縮ですが、私たちの塾(HIRO ACADEMIA)との比較をしていきますね。塾選びの参考になりますと幸いです。
違う点1 完全1対1の授業がメイン
授業をすることで実施している参考書の理解度を深めていきます。
自分一人で参考書をやっていると自己満足しがちな勉強に陥ってしまいます。このような状況ですと、どんだけ参考書を行っても成績を上げることができません。
こうした問題を解決するため当塾では、完全一対一で個別指導を実施しています。
また参考書を実施しているだけだとどこを重点的に行えば良いのか?、参考書に載っていない答が出た際にどのように対応すれば良いのか?ということに困ってしまいます。
こうした問題を解決する際にも、授業で解決していきます。
違う点2 塾内の模試がある
当塾では、大手予備校で実施される模試に加えて、当塾独自で模試を実施しています。
大手予備校で実施される模試ですとなぜ間違えたのか?、などの分析を自分でしていくことになりますが、多くの場合うまくその模試をいかすことができていません。
当塾で実施する模試については、どのように模試を活用するかのフォローアップも最後までしていきます。
また、この模試の結果を踏まえて、普段の指導にあてていきます。
違う点3 月1での集団での補講
個別だと生徒一人一人に合わせるため進路が独りよがりになりがちです。また、復習がたまってしまったりと問題が発生してしまいます。
そうした、問題を解消すべく当塾では月に一度補講の日程を用意しております。そのためいつまでたってもできるようにならない・・・という問題を解消できます。
違う点4 記述力、考える力に力点を置いている
当塾では記述力や日々の自分の勉強を振り返っていくという点を重要視しています。
具体的には毎日の勉強を終わった後に振り返りをしてもらったり、日々の計画表を自分自身で立てたりすることです。書く力や考える力というのは伸ばしづらいのですが、このように自分のことを考えることによって、かんがえる力を伸ばしていきます。
このような考える力や記述力は短期的には目に見えないものですが、長期にわたって、自身の学力や考える力を上げることができるのです。
特にこれからの入試のことを考えるのであれば、考える力は必要不可欠です。こうした力なしで大学入試を迎えることはできません。
当塾ではこうした力を鍛えていくために、考える力の指導を行っています。
違う点5 夏、冬で合宿の実施
当塾では、夏と冬に合宿を行っています。 一日中生徒と一緒にいてどのように勉強をしていくのか?ムダな勉強の仕方はないか?という点を細かく確認していきます。
合宿について詳しくはこちらをご確認ください。
https://hiroacademia.jpn.com/news/2019summer-school-trip/
https://hiroacademia.jpn.com/news/2018-19%e5%b9%b4%e5%b9%b4%e8%b6%8a%e3%81%97%e5%90%88%e5%ae%bf%e3%81%ae%e5%a0%b1%e5%91%8a/
https://hiroacademia.jpn.com/news/study-training/
当塾の料金は?
多くの塾生が選択する早慶ダブルコースが78,000円(税別)となっています。
プラスで小論文の授業をつけたり、自分の苦手な科目の授業を追加でお願いする生徒も多いです。当塾のデメリットとは?
当塾は他の大手の塾さんとは違って、できてから10年程度の比較的新しい塾です。そのため、大手の塾さんと比べて、至らない点があるかもしれません。
その点は事前にご了承ください。
早慶受験でお困りであればまずはカウンセリングへ
ただその分生徒の距離感は他の塾よりも近く、ちょっとした相談もしやすい環境となっております。塾に行っても質問ができない・・何をしていいか困っているなど、ご相談がありましたらお気軽にこちらより相談してください。










 ここくらいまで考えれば、状況がつかめてきますね!
ここくらいまで考えれば、状況がつかめてきますね!
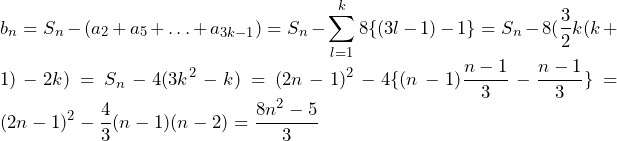 …(答)(n=1のときも成立)
…(答)(n=1のときも成立)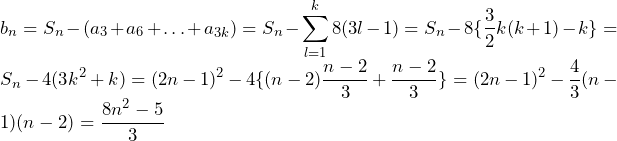 …(答)(n=2のときも成り立つ。)
…(答)(n=2のときも成り立つ。)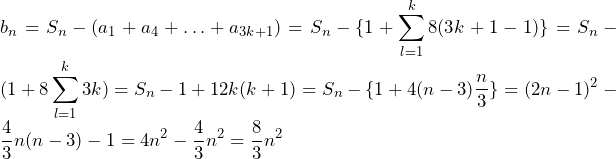 …(答)
…(答)