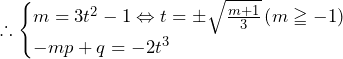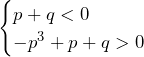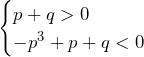2016年早稲田大学理工|過去問徹底研究 大問5 方針の立て方 (1) 問題で与えられた条件を書き下すのみ.点Pに関する条件は,線分APの長さが2のみであるため,これを書き下す.すると,の式となるため,の条件を加えて図示すれば答えとなる. (2) 立体図形上の点に関する問題であるため,ベクトルで考え
- …続きを読む
-
2016年早稲田大学理工|過去問徹底研究 大問5
方針の立て方
(1)
問題で与えられた条件を書き下すのみ.点Pに関する条件は,線分APの長さが2のみであるため,これを書き下す.すると, の式となるため,
の式となるため, の条件
の条件 を加えて図示すれば答えとなる.
を加えて図示すれば答えとなる.(2)
立体図形上の点に関する問題であるため,ベクトルで考える.後は自分で置いた文字(本解答の場合には )を消去すること(
)を消去すること( にも条件がついていることに注意!)と,問題で与えられた条件
にも条件がついていることに注意!)と,問題で与えられた条件 を加えれば答えとなる.
を加えれば答えとなる.(3)
切り口は円であるため,半径を求めればよい.半径は原点と最遠点との距離になる.最遠点は自明に図形 上にあるので,図形
上にあるので,図形 上の点を文字で表し,その最大値を求めればよい.
上の点を文字で表し,その最大値を求めればよい.(4)
積分するだけ.解答例
(1)
APの長さが2のため, .
.
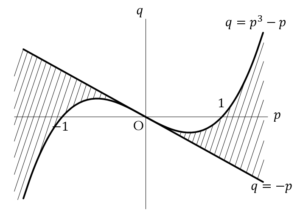
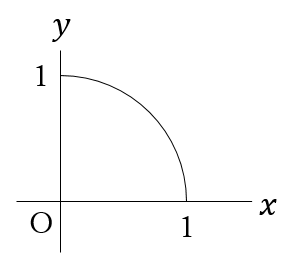
 で図示すると,
で図示すると,

(上図が答え)(2)
AP上の点Qは,
 を満たす.
を満たす.


上二式より, .
. より,
より, .また,
.また, より,
より, .
.
 (
( かつ
かつ かつ
かつ )……(答)
)……(答)(3)
 を
を で切ったとき,点
で切ったとき,点 から最も遠い点を考える.
から最も遠い点を考える.
 と
と の交線上の点は,
の交線上の点は,
 (ただし,
(ただし, かつ
かつ かつ
かつ )と表せる.
)と表せる.
点 との距離は,
との距離は,
 とおくと,
とおくと,

 で
で
 のとき
のとき となり,距離の最大値は
となり,距離の最大値は のときの
のときの となる.
となる.
 のとき,増減表を描くと,
のとき,増減表を描くと,














よって,最大値となりうるのは
 か
か のとき.
のとき.
 のとき,距離は,
のとき,距離は, となり,
となり, のとき,距離は,
のとき,距離は, となる.
となる.
 より,距離の最大値は,
より,距離の最大値は,

 のときの結果と合わせると,距離の最大値は,
のときの結果と合わせると,距離の最大値は,

 ……(答)
……(答)(4)
![Rendered by QuickLaTeX.com V=\int_{0}^{1}S\left(t\right)dt=\int_{0}^{\frac{1}{2}}{3\pi\left(1-t\right)^2}dt+\int_{\frac{1}{2}}^{1}\pi\left(1-t^2\right)dt=\left[-\pi\left(1-t\right)^3\right]_0^{\frac{1}{2}}+\left[\pi\left(t-\frac{1}{3}t^3\right)\right]_{\frac{1}{2}}^1=\frac{13}{12}\pi](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmgAAABMAQAAAADxNnbtAAAAAnRSTlMAAHaTzTgAAAAbSURBVBgZ7cEBAQAAAIKg/q92SMAAAAAAAOBYFygAAZwhRUoAAAAASUVORK5CYII=) ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。







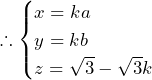
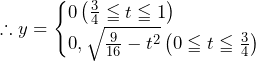 で
で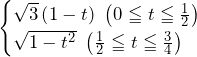
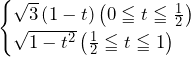
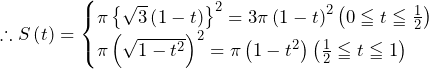 ……(答)
……(答)![Rendered by QuickLaTeX.com V=\int_{0}^{1}S\left(t\right)dt=\int_{0}^{\frac{1}{2}}{3\pi\left(1-t\right)^2}dt+\int_{\frac{1}{2}}^{1}\pi\left(1-t^2\right)dt=\left[-\pi\left(1-t\right)^3\right]_0^{\frac{1}{2}}+\left[\pi\left(t-\frac{1}{3}t^3\right)\right]_{\frac{1}{2}}^1=\frac{13}{12}\pi](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-23dadfd7a2f6b605eb35cb7bc70d9990_l3.png) ……(答)
……(答)