2016年慶應大学総合政策数学|過去問徹底研究大問6 方針の立て方 簡単に解ける公式や規則性等は見つけられないので,地道に書き出して考える.(2)でさえ高々16通りを考えればよいのだから,綺麗に解くことに時間を割くよりは,ケアレスミスにだけ気を付けてしらみつぶししたほうがコスパが良い. 解答例 (6
- …続きを読む
-
2016年慶應大学総合政策数学|過去問徹底研究大問6
方針の立て方
簡単に解ける公式や規則性等は見つけられないので,地道に書き出して考える.(2)でさえ高々16通りを考えればよいのだから,綺麗に解くことに時間を割くよりは,ケアレスミスにだけ気を付けてしらみつぶししたほうがコスパが良い.
解答例
(65)(66)……
(67)(68)……
(69)(70)……
(71)(72)(73)(74)……
(75)(76)(77)(78)……
(79)(80)(81)(82)……
(83)(84)(85)(86)……
解説
(1)
政党Aについて:YNY,YYNとY↔Nで入れ替えた4通り. ……(答)
……(答)
政党Bについて:NYY,YYNとY↔Nで入れ替えた4通り. ……(答)
……(答)
政党Cについて:NYY,YNYとY↔Nで入れ替えた4通り. ……(答)
……(答)(2)
YとNの並びを の順で表す.
の順で表す.
政党Aについて:YYYN,NYYN(Y↔Nの入れ替えは含まない)と,YYNY,YNYY,YNYN,YYNNおよびY↔Nで入れ替えた計10通り. ……(答)
……(答)
政党Bについて:YYNY,YNNY(Y↔Nの入れ替えは含まない)と,NYYY,YYNNおよびY↔Nで入れ替えた計6通り. ……(答)
……(答)
政党 について:YNYY,YNNY(Y↔Nの入れ替えは含まない)と,NYYY,YNYNおよびY↔Nで入れ替えた計6通り.
について:YNYY,YNNY(Y↔Nの入れ替えは含まない)と,NYYY,YNYNおよびY↔Nで入れ替えた計6通り. ……(答)
……(答)
政党 について:NYYY,NYYN(Y↔Nの入れ替えは含まない)の2通り.
について:NYYY,NYYN(Y↔Nの入れ替えは含まない)の2通り. ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。









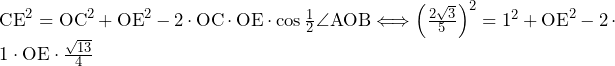
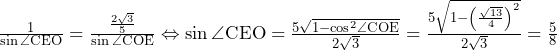
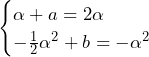
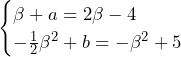
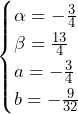
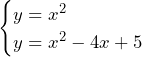
![Rendered by QuickLaTeX.com \int_{-\frac{3}{4}}^{\frac{5}{4}}\left\{x^2-\left(\frac{1}{2}x^2-\frac{3}{4}x-\frac{9}{32}\right)\right\}dx+\int_{\frac{5}{4}}^{\frac{13}{4}}\left\{\left(x^2-4x+5\right)-\left(\frac{1}{2}x^2-\frac{3}{4}x-\frac{9}{32}\right)\right\}dx=\int_{-\frac{3}{4}}^{\frac{5}{4}}\left(\frac{1}{2}x^2+\frac{3}{4}x+\frac{9}{32}\right)dx+\int_{\frac{5}{4}}^{\frac{13}{4}}\left(\frac{1}{2}x^2-\frac{13}{4}x+\frac{169}{32}\right)dx=\left[\frac{1}{6}x^3+\frac{3}{8}x^2+\frac{9}{32}x\right]_{-\frac{3}{4}}^{\frac{5}{4}}+\left[\frac{1}{6}x^3-\frac{13}{8}x^2+\frac{169}{32}x\right]_{\frac{5}{4}}^{\frac{13}{4}}=\frac{4}{3}+\frac{4}{3}=\frac{8}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-43566093742bcefede7fed31bdf18173_l3.png) ……(答)
……(答)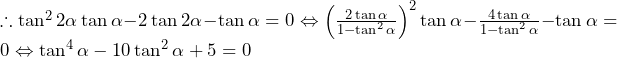
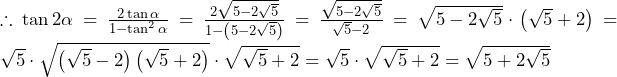
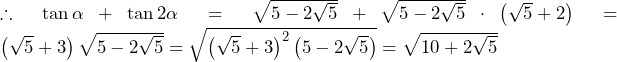 ……(答)
……(答)