「数学の問題を解くとき、どうやって考えればいいのか分からない…」そんな悩みを持つ受験生の方は多いはず。 特に「公式や定理は頭に入れているつもりだけれど、実際の問題にどう当てはめるかがわからない」と感じる人にとっては、深刻な課題かもしれません。 そこでおすすめしたいのが『解法のエウレカ』シリーズ。 解
- …続きを読む
- 「数学の問題を解くとき、どうやって考えればいいのか分からない…」そんな悩みを持つ受験生の方は多いはず。
特に「公式や定理は頭に入れているつもりだけれど、実際の問題にどう当てはめるかがわからない」と感じる人にとっては、深刻な課題かもしれません。
そこでおすすめしたいのが『解法のエウレカ』シリーズ。解法のエウレカは、数学I・A編、そしてついに待望の数学II・B編が発売され、多くの受験生から注目を集めています。
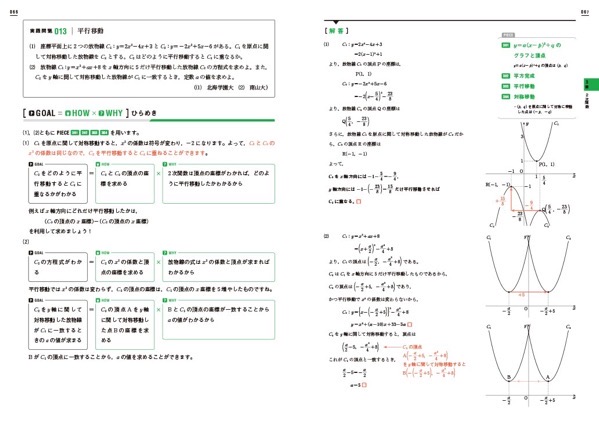
「HOW(どのように解くか)」と「WHY(なぜその解き方を使うのか)」、そして「Piece(必要な公式・知識)」という3つの視点から問題を解きほぐす仕組みが特徴。
難関大レベルの問題に至る前に、しっかりと思考プロセスを身につけられる教材として人気を得ています。
この記事では、実際に使った感想や効果的な使い方を含めて、本書の特徴や活用法を徹底的に解説していきます。
[toc]解法のエウレカの概要
『解法のエウレカ』は、フォーカスゴールドで知られる竹内先生と、『部分点で稼ぐ』などで有名な小倉先生がタッグを組んだ問題集です。2022年頃に発売された数学I・A編、そして約1年後にリリースされた待望の数学II・B編は、多くの受験生から支持され、重版がかかるほどの人気教材となっています。
本書の最大の特徴は、「HOW(どのように解くのか)とWHY(なぜその方法なのか)、そしてPiece(必要な公式や知識)」を重視した解説構成にあります。単に「この公式を使います」「こうすれば解けます」という短絡的な手順の羅列ではなく、「なぜその公式が必要になるのか?」、「ゴールから逆算してどのプロセスを踏むのか?」という思考回路を言語化し、数学的な問題解法の思いつき方を身につけさせてくれるのです。
- 対象レベル:やや発展レベル(おおよそMARCH、関関同立、地方国公立大向け)
- 到達レベル:標準入試問題で合格点を狙える。難関大(旧帝大など)を本命とする人にはやや不足。
- 問題数:数学I・A/II・Bともに数百問ほど(教科書レベル+実践レベル)
- 特徴:HOW・WHY・Pieceの3つを繰り返し学んで思考力を養うスタイル。
「網羅系の青チャートやフォーカスゴールドを使ってきたが、問題数の多さに挫折してしまう…」
「数学的な考え方が掴めず、公式は覚えているのに実践で使えない…」という悩みを抱える人に、本書が強力な味方になってくれるでしょう。解法のエウレカの特徴
解法のエウレカが持つ最大の特徴は、「どう解くか(HOW)」「なぜそう解くか(WHY)」「必要な公式・知識(Piece)」を常に意識させる構成です。

① HOW & WHYで思考プロセスを明確化

これまでの多くの参考書は、「公式をこう使えば解ける」「これが定番解法」と解説して終わる場合が少なくありませんでした。
しかし、解法のエウレカでは、公式の使いどころを示すだけでなく、「なぜその解法に至るのか、ほかのアプローチはないのか」といった部分を丁寧に掘り下げています。
「解法暗記で乗り切ろうとしている」状態から、「問題を見たときにどんな手札を思い出すべきか、どう判断するか」を学ぶことで、初見問題への対応力を高めようとする意図が感じられます。いわゆる「数学的なセンス」は突発的に生まれるものではありません。HOW & WHYを積み重ねることで、“ひらめき”を自分で作る土台を築くのがエウレカ流の勉強法です。

② Piece:必要な公式・知識を整理
本書では、各章の前半に「Piece」と呼ばれる、問題を解くための前提知識や公式がまとまっています。
基礎知識が抜け漏れになっていないかを確認しつつ、その公式がどんなシーンで使えるかを具体的な例とともに学べるのがメリットです。「基礎問題精講」や「青チャート」のコンパスレベルは既に一度やったけれど、いまいち頭の中で整理されていない方にこそ、このPieceパートが効率的に力をつける助けになります。
③ 実践問題での活用法がわかる
HOW & WHY、Pieceを押さえたら、実際に問題を解いてその考え方を身につけるステップへ進みます。
「最終的なゴールから何を使えば到達できるか?」という視点を大切にするため、どの実践問題でも、ゴールから逆算する思考を逐一解説してくれます。結果的に、単に“公式を覚えた”だけで終わらず、「問題文からゴールまでをどのようにつなげるか」を学べるため、入試で初めて見る問題にも落ち着いて取り組みやすくなります。
このメソッドは、確率の思考力や図形・ベクトルの応用力など、受験生が苦手としやすい分野で特に威力を発揮します。難易度・到達レベル
- 到達可能レベル:MARCH~中堅国公立大(偏差値55~60台程度)
- 旧帝大や難関国立大(東大・京大など)向けとしてはやや不足
解法のエウレカは、「数学がそれほど得意ではないが、ある程度解けるようになりたい」人に最適です。
青チャートなどの網羅系参考書を一通り終えたあとの次のステップとしてもよいですし、
基礎はそれなりに固まっているけど、「入試本番レベルの問題でどう戦えばいいのか」を知りたい段階にぴったり。実際には、MARCH・関関同立レベル、あるいは偏差値50後半~60台前半くらいの私立・国公立大学に的を絞るなら、本書で十分合格点が狙えます。
ただし、難問奇問を出すような旧帝大や東工大などを目指すのであれば、エウレカで思考法を学んだ後、もうワンステップ上の問題演習(例えば「重要問題集」や「過去問」、さらに難関大対策用の問題集など)が必要になってくるでしょう。解法のエウレカの使い方
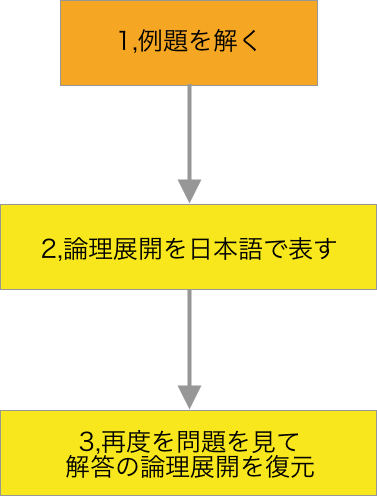
ここからは、本書を使って効率よく実力を伸ばすためのステップを紹介します。
[ptimeline]
従来の「解法暗記型」学習から卒業し、本質的に数学力を上げるコツを押さえましょう。
[ti label="STEP1" title="基礎知識の確認(Pieceパート)"]
まずは各セクションの冒頭で整理されている「Piece」をしっかり押さえましょう。
公式・定理はただ暗記するだけでなく、「どんな問題で役に立つのか」まで理解するのがポイントです。
[/ti]
[ti label="STEP2" title="HOWとWHYを意識して実践問題を解く"]
問題を解くとき、いきなり解法に飛びつかず、「ゴール(求めたいもの)に必要な情報は何か?」や「どんな公式を使うと繋がるか?」を考えるクセをつけましょう。
解説ではWHY(なぜその公式を使うか)が詳しく書かれているので、理解を深めるうえで絶対に飛ばさないように。
[/ti]
[ti label="STEP3" title="解説の読み込みで”自分の考え”と比較"]
解いてみたあとは必ず解説を熟読。自分のアプローチと照らし合わせて、「なぜ違うルートで解けたのか」「なぜこの方法が最短なのか」を客観的に見直します。
解説に載っている「別解」も含めて検討すると、応用力がさらに高まります。
[/ti]
[ti label="STEP4" title="間違えた問題は時間をおいて再チャレンジ"]
数学力は一朝一夕で身につかないもの。間違えた問題は、ある程度時間を空けてから再度挑戦しましょう。
ひとつの問題を複数回繰り返すほうが、あれこれ手を広げるより効果的です。
[/ti]
[ti label="STEP5" title="過去問・他教材で定着度を確認"]
本書を1周(目安として1ヶ月程度集中すれば終えられる分量)したら、次は志望校の過去問やもう少し難易度の高い問題集にトライ。
解法のエウレカで培った思考プロセスを、実際の試験形式で試してみましょう。
[/ti]
[/ptimeline]他教材との接続: 「青チャートなどで基礎は一通り学んだけれど、入試問題を解くと手が止まってしまう」層に特におすすめ。
「さらに旧帝大を狙う!」「医学部を目指す!」という場合は、本書を仕上げたうえで、一段上の参考書や難度の高い過去問演習に移りましょう。メリット・デメリット
それでは、解法のエウレカのメリットデメリットを見ていきましょう。
メリット- 問題の選択と解説が適切:不要な難問・奇問が少なく、適度なレベルの実践問題が厳選されている。
- HOW & WHYの徹底:解放暗記を卒業し、思考プロセスを学べる。
- 基礎~標準の橋渡し:青チャートレベルの知識を実際の入試問題レベルへ繋げやすい。
- 独学でも理解しやすい:解説が丁寧なので、塾や予備校がなくても使いこなしやすい。
解法のエウレカは、とりわけ「数学の考え方を身につけたい」という受験生に向いています。
学習者が疑問に思いがちな点(「そもそもこの公式はどんなときに使うの?」「途中式の意義は?」など)を先回りして解説しているため、自学自習でも挫折しにくい点が大きな強み。
実際、複数のレビューでも「問題の難易度がちょうどよく、自分の弱点をカバーしやすかった」「初めて解説を読んで”納得”できた」という声が多く見られます。デメリット- 旧帝大レベルの難問には対応しきれない:超難関校を目指すなら追加教材が必須。
- 3C分野が非対応:理系で数IIIが必要な場合には不足。
- 解説が丁寧ゆえに時間がかかる:一題一題の解説が充実しすぎて、短期間でサッと全問演習するには根気が必要。
トップレベルの理系大学(京大、東大、医学部など)を本格的に志望する場合、解法のエウレカだけでは足りず、さらに難問を扱う問題集や演習書で実践力を底上げする必要があります。
また、数IIIや複素数平面などは扱われていないため、理系や医学部などで数IIIを使う受験生は本書でIIBを学んだ後、数IIIの別教材を必須でこなしてください。他の教材・参考書との比較
本書を他の有名問題集や参考書と比較することで、どのように活用すればいいかがより明確になります。
青チャートとの比較
「青チャート」は問題数・網羅性に優れ、教科書レベルから難関大まで幅広くカバーしています。一方で、解説が簡潔なので、解法暗記に陥りやすいという声も多いです。
青チャートをやり込めば、数学力は確かに上がるものの、問題数が膨大で「どこから手をつければいいのか分からない」ケースも。そこでエウレカは、厳選された標準レベルの問題と丁寧なHOW&WHY解説で、「公式を暗記して終わりではなく、なぜこう解くのか」を学べるのがメリット。
どちらか一冊だけに絞るとしたら、短期間で思考の質を上げたい人はエウレカ、網羅的に大量演習をこなす余裕がある人は青チャート、という使い分けがいいでしょう。青チャートを一通り終えたのに入試問題が解けなかった…という人は
解法のエウレカで「思考プロセス」を補強するのがおすすめです。
フォーカスゴールドとの比較
フォーカスゴールドも、網羅系問題集として高い評価を受けています。実際、本書の著者でもある竹内先生はフォーカスゴールドにも深く関わられているため、両方に通じるノウハウが感じられます。
大きな違いは、フォーカスゴールドはある程度解説がシンプルで演習量が多いのに対し、エウレカは「解説がさらに丁寧で、問題数はややコンパクト」です。「フォーカスゴールドは使ってみたが、まだ問題に手が止まることが多い」と感じる人には、エウレカで思考回路を学ぶ価値が大きいといえます。
逆に、「エウレカを終えて余力があれば、フォーカスゴールドで総仕上げ演習」という流れもおすすめです。フォーカスゴールドは網羅性重視、
解法のエウレカは思考プロセス重視という違いがあります。 エウレカは網羅系参考書とうまい具合に併用していくのが合格の鍵です。
エウレカは網羅系参考書とうまい具合に併用していくのが合格の鍵です。重要問題集との比較
「重要問題集」は難関校を含め、実際の入試頻出問題を中心にした良問が多数載っており、ある程度数学力がついてきた人の仕上げ向けです。
解説はポイントをまとめた形なので、初心者にはやや難解な場合があります。エウレカで「公式の使い方」や「問題へのアプローチの仕方」を身につけたら、その次のステップとして重要問題集に取り組む、というルートも一般的です。
エウレカ → 重要問題集 → 志望校の過去問、という流れで、演習量と理解度の両方を高めていくと、難関大学対策まで一貫性を持って進められるでしょう。重要問題集は問題の質が高く、演習量も豊富。
ただし、最初に使うと挫折しがちなため、
解法のエウレカを踏んでから入る人も多いです。
こんな人におすすめ
『解法のエウレカ』は以下のような方に特におすすめです。
- 「数学が苦手意識はあるが、ある程度得点できるようになりたい」
- 「青チャートの網羅性は一通りこなしたが、まだ入試問題で歯が立たない」
- 「How(解き方)とWhy(理由)を明確に理解して、初見問題にも応用したい」
- 「医学部や難関大学を目指すが、まず標準レベルの土台をしっかり固めたい」
- 「フォーカスゴールドや他の問題集で挫折しがちだった」
特に、医学部受験などで数学が足を引っ張っているという受験生、共通テスト~MARCHクラスを狙う受験生には有効です。
最短で「数学の点数を底上げしたい」「入試本番で解ける問題を確実に取りたい」というケースでは、大いに活躍してくれるでしょう。まとめ:数学の思考力を身につけるための最短ルート
『解法のエウレカ』は、「HOW(どうやって)」「WHY(なぜ)」を重視することで、数学を論理的に理解し、初見問題でも応用できる力を養う効率重視の問題集です。
特に「公式を覚えるだけでなく、問題を見た瞬間にどうアプローチを組み立てるか」を掴むために、丁寧に解説が書かれているので、独学でも取り組みやすい構成となっています。
基礎レベルがある程度できた段階(青チャートや教科書の基本問題をこなした後など)で本書に取り組むと、まさに入試で求められる発想力・思考力を磨くのにうってつけです。一方、旧帝大・東大・京大などトップ難関校の超難問に挑む場合は、本書だけで全てを網羅するのは難しいかもしれません。
しかし、エウレカで「合否を左右する標準~やや難レベルの問題」を確実にモノにしたうえで追加の演習をこなすことで、最難関にも対応できる素地が築けるでしょう。ぜひ、本記事の内容を参考に、『解法のエウレカ』をフル活用してみてください。
考え方を重視して学ぶことで、徐々に「数学って面白いかも」「もっと上のレベルにもいけそうだ」と感じられるはず。
短期間で得点力を伸ばし、志望校合格や成績アップに大きく近づくための一歩を、ここからスタートしましょう!