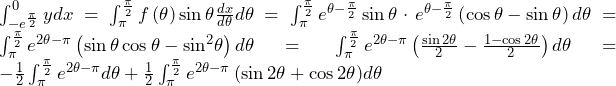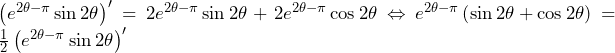方針の立て方 (1) Aの箱に他の箱からのボールの追加をするわけだが,それぞれの箱(AとA以外)で黒ボールと白ボールの割合が違う.これこそがこの問題の難所である.数学においては「難所がある場合にはそれを分割する」ことが基本的な考え方である.そのため,Aにそもそも入っていたボールと,後からAに入ってき
- …続きを読む
- 方針の立て方
(1)
Aの箱に他の箱からのボールの追加をするわけだが,それぞれの箱(AとA以外)で黒ボールと白ボールの割合が違う.これこそがこの問題の難所である.数学においては「難所がある場合にはそれを分割する」ことが基本的な考え方である.そのため,Aにそもそも入っていたボールと,後からAに入ってきたボールとて分割して考えるという方針を立てる.(2)
前問と同様それぞれの箱で黒ボールと白ボールの割合が違うことから,これらを分割して考える必要があると判断する.ただし,本問の場合には交換の度に箱E内の割合が変わってしまうことに注意.ここも分割することになる.よって,本解答のような,交換の度に確率を考えるという方針になる.解答例
(1)(2)(3)(4)……
(5)(6)(7)(8)……
(9)(10)(11)(12)……
(13)(14)(15)(16)……
解説
(1)
最終的に計19個のボールがAに入っている.最初にAに入っていた黒ボールを取り出す確率と,後から加えられた黒ボールを取り出す確率を求める.
・最初にAに入っていた黒ボールを取り出す確率
19個のボールの中から最初に入っていた7個の黒ボールのどれかを取り出す確率のため
・後から加えられた黒ボールを取り出す確率
19個あるボールの中から後から加えられたボールを取り出す確率が であり,後から加えられたボールの中から1個のボールを取り出したときに,それが黒ボールである確率は
であり,後から加えられたボールの中から1個のボールを取り出したときに,それが黒ボールである確率は である.これらは独立であるため,後から加えられた黒ボールを取り出す確率は,
である.これらは独立であるため,後から加えられた黒ボールを取り出す確率は, となる.
となる.
よって,求める確率は,
 ……(答)
……(答)(2)
EとFの箱の交換の後で,Eの箱から1個のボールを無作為に取り出したときにそれが黒ボールである確率は,前問と同様に場合分けして考えると,
・最初からEに入っていた黒ボールを取り出す確率
10個あるボールの中から最初からEに入っていたボールを取り出す確率が であり,最初からEに入っていたボールの中から1個のボールを取り出したときに,それが黒ボールである確率は
であり,最初からEに入っていたボールの中から1個のボールを取り出したときに,それが黒ボールである確率は である.これらは独立であるため,最初からEに入っていた黒ボールを取り出す確率は,
である.これらは独立であるため,最初からEに入っていた黒ボールを取り出す確率は, となる.
となる.
・交換によってEに入ってきた黒ボールを取り出す確率
10個あるボールの中から交換によってEに入ってきたボールを取り出す確率が であり,交換によってEに入ってきたボールの中から1個のボールを取り出したときに,それが黒ボールである確率は
であり,交換によってEに入ってきたボールの中から1個のボールを取り出したときに,それが黒ボールである確率は である.これらは独立であるため,最初からEに入っていた黒ボールを取り出す確率は,
である.これらは独立であるため,最初からEに入っていた黒ボールを取り出す確率は, となる.
となる.
よって,EとFの箱の交換の後で,Eの箱から1個のボールを無作為に取り出したときにそれが黒ボールである確率は である.この確率を
である.この確率を とおく.
とおく.
次に,EとGの箱の交換の後で,Eの箱から1個のボールを無作為に取り出したときにそれが黒ボールである確率を求める.この交換の前にEに入っていた黒ボールを取り出す確率と交換によってEに入ってきた黒ボールを取り出す確率を場合分けして考えて,それらの確率を足し合わせると,

となる.この確率を とおく.
とおく.
次に,EとHの箱の交換の後で,Eの箱から1個のボールを無作為に取り出したときにそれが黒ボールである確率を求める.この交換の前にEに入っていた黒ボールを取り出す確率と交換によってEに入ってきた黒ボールを取り出す確率を場合分けして考えて,それらの確率を足し合わせると,

となる.この確率を とおく.
とおく. こそが求める確率である.
こそが求める確率である. と
と を代入すれば,
を代入すれば,
 ……(答)
……(答)






 となってしまい,なぜ不適かが分かり,解法が思いつくだろう.
となってしまい,なぜ不適かが分かり,解法が思いつくだろう.
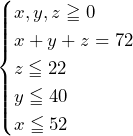
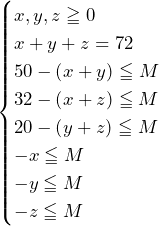
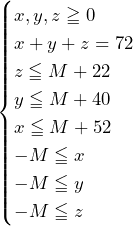
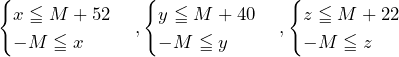
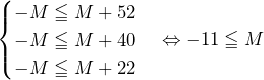
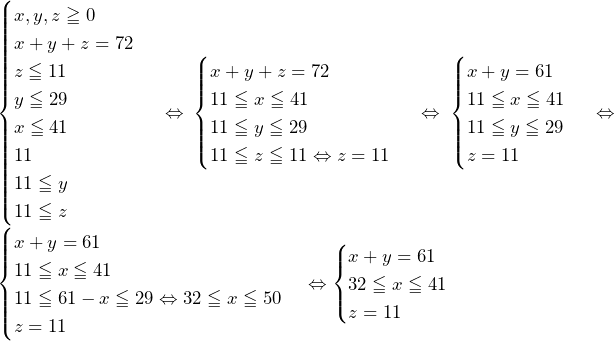
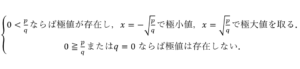
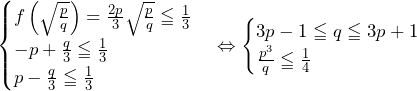
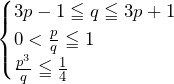 ……(答)
……(答)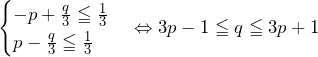
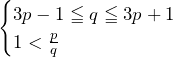 ……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.
……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.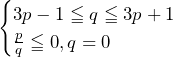 ……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.
……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.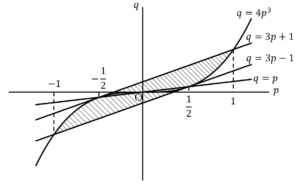
![Rendered by QuickLaTeX.com 2\left[\int_{0}^{\frac{1}{2}}\left\{3p+1-\left(3p-1\right)\right\}dp+\int_{\frac{1}{2}}^{1}\left(3p+1-4p^3\right)dp\right]=2\left\{\left[2p\right]_0^{\frac{1}{2}}+\left[-p^4+\frac{3}{2}p^2+p\right]_{\frac{1}{2}}^1\right\}=\frac{27}{8}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-f56368e0ec425cd83fbebcfd5460687d_l3.png) ……(答)
……(答)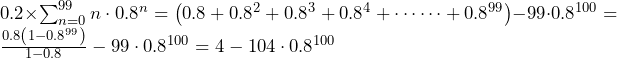
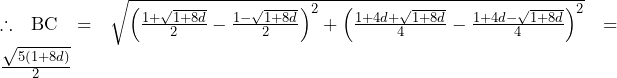
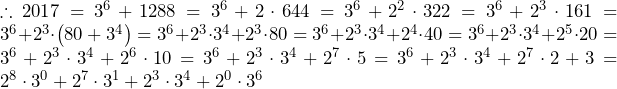 ……(答)
……(答)
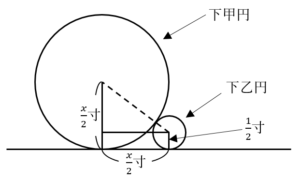



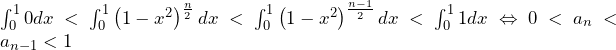
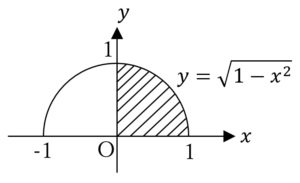
![Rendered by QuickLaTeX.com a_n=\int_{0}^{1}\left(1-x^2\right)^\frac{n}{2}dx=\int_{0}^{1}{\left(x\right)^\prime\left(1-x^2\right)^\frac{n}{2}}dx=\left[x\left(1-x^2\right)^\frac{n}{2}\right]_0^1-\int_{0}^{1}{x\cdot\frac{n}{2}\left(1-x^2\right)^\frac{n-2}{2}\cdot\left(-2x\right)}dx=n\int_{0}^{1}{x^2\left(1-x^2\right)^\frac{n-2}{2}}dx](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-3383a4e3a41de53f568ac6beddb7b89b_l3.png)
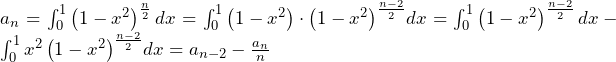
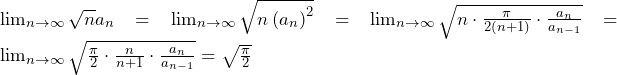 ……(答)
……(答)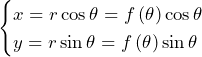
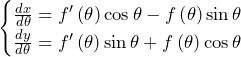
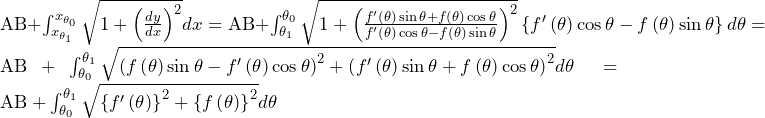
![Rendered by QuickLaTeX.com \mathrm{AB}+\int_{\theta_0}^{\theta_1}\sqrt{\left\{f^\prime\left(\theta\right)\right\}^2+\left\{f\left(\theta\right)\right\}^2}d\theta=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}\sqrt{\left\{\alpha\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2+\left\{\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2}d\theta\bigm=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}{\sqrt{1+\alpha^2}\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}}d\theta=\frac{v}{\sqrt{v^2-1}}+\sqrt{1+\alpha^2}\beta\left[\frac{1}{\alpha}e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right]_{\frac{\pi}{2}}^{\theta_1}\bigm=\frac{v}{\sqrt{v^2-1}}-\frac{\beta}{\alpha}\sqrt{1+\alpha^2}+\frac{\beta}{\alpha}\sqrt{1+\alpha^2}e^{\alpha\left(\theta_1-\frac{\pi}{2}\right)}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-3251c46fb035b1c6f3d900fd751c1cf5_l3.png)
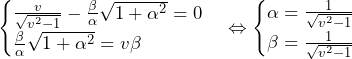 ……(答)
……(答)