早稲田大学理工過去問徹底研究 2018年 大問1 方針の立て方 (1) 実際にP,A,Bの位置関係を図に描いてみると解法を得られる.「3点を結ぶと三角形をなす」ことと,「3点が一直線上にない」ことが同値であることは頻出のためおさえておくこと. (2) 前問と同様にP,A,Bの位置関係を図に描いてみる
- …続きを読む
-
早稲田大学理工過去問徹底研究 2018年 大問1
方針の立て方
(1)
実際にP,A,Bの位置関係を図に描いてみると解法を得られる.「3点を結ぶと三角形をなす」ことと,「3点が一直線上にない」ことが同値であることは頻出のためおさえておくこと.(2)
前問と同様にP,A,Bの位置関係を図に描いてみると,ABを底辺と見ると都合がいいことが分かる.複素共役な2つの複素数は,複素数平面上では実軸対称となることは,複素数と図形の融合問題では頻出の考え方のためおさえておくこと.(3)
外心の定義と外心の作図の仕方を考えれば解法を得られる.解答例
(1)
3次方程式 の解は,
の解は, の3つ.
の3つ.
3点P,A,Bが三角形をなすには,3点P,A,Bが一直線上になければ必要十分.そのためには, が虚数解であり(
が虚数解であり( が実数解ならば,
が実数解ならば, が実数であるため,3点P,A,Bが一直線上に並んでしまう),かつ
が実数であるため,3点P,A,Bが一直線上に並んでしまう),かつ の実部が
の実部が でなければ必要十分.
でなければ必要十分.
 を解くと,
を解くと, であるから,求める条件は,
であるから,求める条件は,
 ……(答)
……(答)(2)

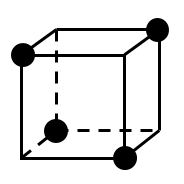
3点P,A,Bの位置関係は上図の通り.
 (
( (1))より,
(1))より,
 ……(答)
……(答)(3)
三角形の外接円の中心は,各辺の垂直二等分線の交点である.
辺ABの垂直二等分線は,実軸である.よって,求める中心Qは (
( は実数)とおける.QとP,QとAの距離が等しいことより,
は実数)とおける.QとP,QとAの距離が等しいことより,

が成り立ち,これを解くと, ……(答)
……(答)
また,半径 は,
は,

 (
( (1))より,
(1))より,
 ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。







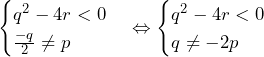 ……(答)
……(答)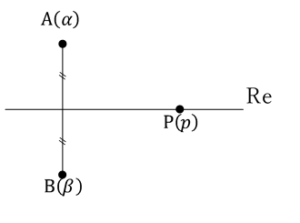
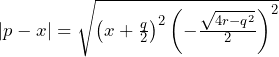

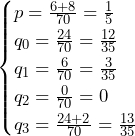 ……(答)
……(答)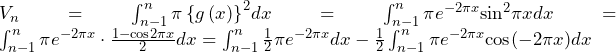
![Rendered by QuickLaTeX.com \int_{n-1}^{n}{\pi e^{-2\pi x}\cos{\left(-2\pi x\right)}}dx=-\frac{1}{2}\int_{-2\left(n-1\right)\pi}^{-2n\pi}{e^y\cos{y}}dy\bigm=-\frac{1}{2}\left[\frac{1}{2}e^y\left(\cos{y}+\sin{y}\right)\right]_{-2\left(n-1\right)\pi}^{-2n\pi}\bigm=-\frac{1}{4}\left(e^{-2n\pi}-e^{-2\left(n-1\right)\pi}\right)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-df13329429bcde4e2ecc7f39a38e588b_l3.png)
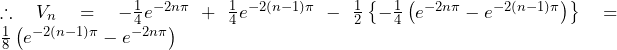 ……(答)
……(答)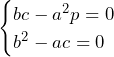
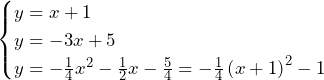
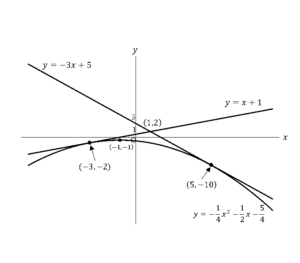
![Rendered by QuickLaTeX.com \int_{-3}^{1}\left\{\left(x+1\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx+\int_{1}^{5}\left\{\left(-3x+5\right)-\left(-\frac{1}{4}x^2-\frac{1}{2}x-\frac{5}{4}\right)\right\}dx\bigm=\left[\frac{1}{12}x^3+\frac{3}{4}x^2+\frac{9}{4}x\right]_{-3}^1+\left[\frac{1}{12}x^3-\frac{5}{4}x^2+\frac{25}{4}x\right]_1^5=\frac{32}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-bbec6b7afbfd51917ee8a7761b2bc8b3_l3.png) ……(答)
……(答)