方針の立て方 接線については「曲線が接する」の定義通り,接線が一致することを利用する.そのため,接線を求めていく.後は基本的な解法に従えばよいため,特筆事項なし. 解答例 (36)…… (37)(38)…… (39)(40)…… (41)…… (42)(43)…… (44)(45)…… (46)……
- …続きを読む
- 方針の立て方
接線については「曲線が接する」の定義通り,接線が一致することを利用する.そのため,接線を求めていく.後は基本的な解法に従えばよいため,特筆事項なし.解答例
(36)……
(37)(38)……
(39)(40)……
(41)……
(42)(43)……
(44)(45)……
(46)……
(47)……
(48)(49)……
解説
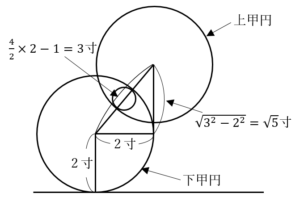
○ ((36)~(38)について)
((36)~(38)について)
 と
と の接点を
の接点を とする.
とする.
 より,点
より,点 での接線は,
での接線は, である.
である.
 より,点
より,点 での接線は,
での接線は, である.
である.
これらが一致するので,

また,点 は
は 上の点のため,
上の点のため, が成り立つ.これらより,
が成り立つ.これらより, と
と を消去すると,
を消去すると,
 ……(答)
……(答)○
 の範囲((39)と(40)について)
の範囲((39)と(40)について)
まず, より,
より,

次に,接点の 座標について,
座標について,

であり,これは正でなくてはならないから,

 に注意して解くと,
に注意して解くと,
 ……(答)
……(答)○
 と
と の交点のx座標((41)~(43)について)
の交点のx座標((41)~(43)について)

 ……(答)
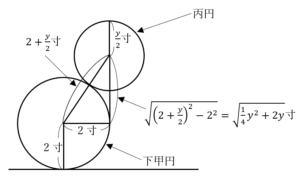
……(答)○領域の面積((44)~(49)について)
![Rendered by QuickLaTeX.com \int_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}\left(q-x^2\right)dx=\int_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}\left\{\left(r+\frac{1}{2}\right)^2-x^2\right\}dx=\left[\left(r+\frac{1}{2}\right)^2x-\frac{1}{3}x^3\right]_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}=\frac{4}{3}r^3+2r^2+r+\frac{1}{6}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmgAAABZAQAAAACiLeXFAAAAAnRSTlMAAHaTzTgAAAAcSURBVBgZ7cEBAQAAAIKg/q92SMAAAAAAAADgRhseAAEu52/QAAAAAElFTkSuQmCC) ……(答)
……(答)






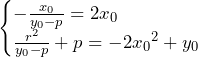
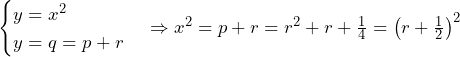
![Rendered by QuickLaTeX.com \int_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}\left(q-x^2\right)dx=\int_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}\left\{\left(r+\frac{1}{2}\right)^2-x^2\right\}dx=\left[\left(r+\frac{1}{2}\right)^2x-\frac{1}{3}x^3\right]_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}=\frac{4}{3}r^3+2r^2+r+\frac{1}{6}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-94aeca5089102bd3c6cc95fc6a86c7e9_l3.png) ……(答)
……(答)
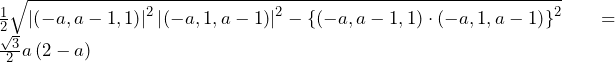
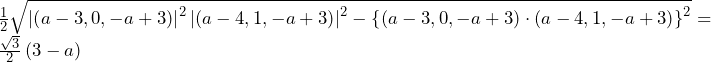
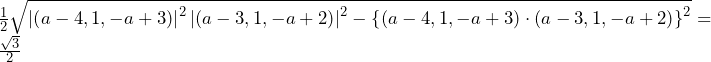
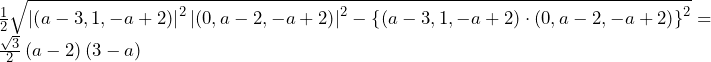
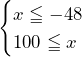 となってしまい,なぜ不適かが分かり,解法が思いつくだろう.
となってしまい,なぜ不適かが分かり,解法が思いつくだろう.
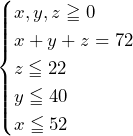
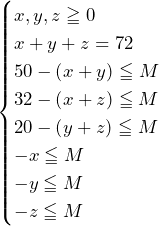
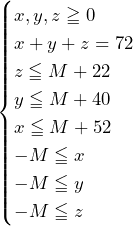
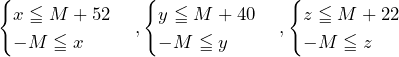
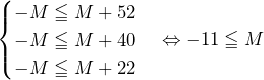
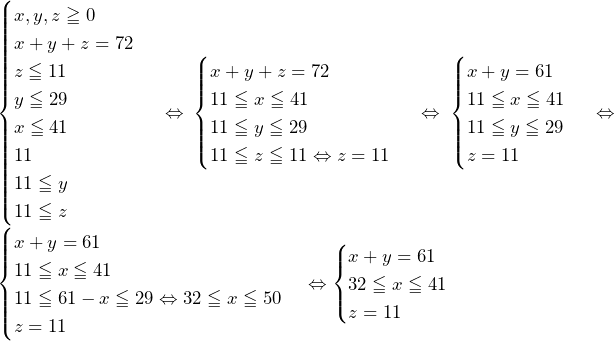
 ……(答)
……(答)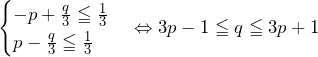
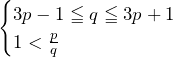 ……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.
……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.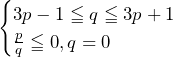 ……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.
……(答) ※(ⅰ)が解ければ解答番号から答えは解かずして分かる.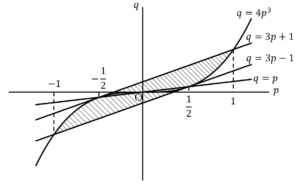
![Rendered by QuickLaTeX.com 2\left[\int_{0}^{\frac{1}{2}}\left\{3p+1-\left(3p-1\right)\right\}dp+\int_{\frac{1}{2}}^{1}\left(3p+1-4p^3\right)dp\right]=2\left\{\left[2p\right]_0^{\frac{1}{2}}+\left[-p^4+\frac{3}{2}p^2+p\right]_{\frac{1}{2}}^1\right\}=\frac{27}{8}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-f56368e0ec425cd83fbebcfd5460687d_l3.png) ……(答)
……(答)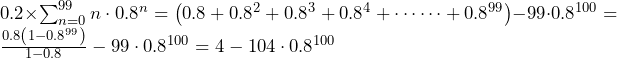
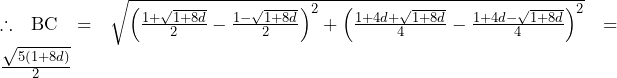
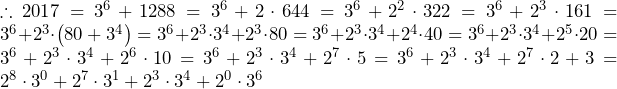 ……(答)
……(答)
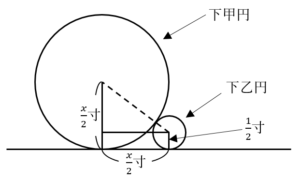

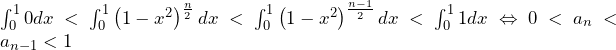
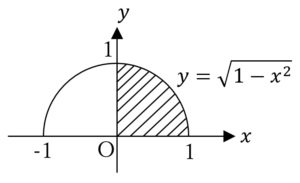
![Rendered by QuickLaTeX.com a_n=\int_{0}^{1}\left(1-x^2\right)^\frac{n}{2}dx=\int_{0}^{1}{\left(x\right)^\prime\left(1-x^2\right)^\frac{n}{2}}dx=\left[x\left(1-x^2\right)^\frac{n}{2}\right]_0^1-\int_{0}^{1}{x\cdot\frac{n}{2}\left(1-x^2\right)^\frac{n-2}{2}\cdot\left(-2x\right)}dx=n\int_{0}^{1}{x^2\left(1-x^2\right)^\frac{n-2}{2}}dx](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-3383a4e3a41de53f568ac6beddb7b89b_l3.png)
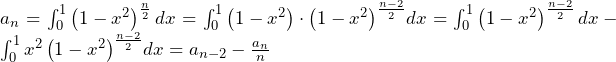
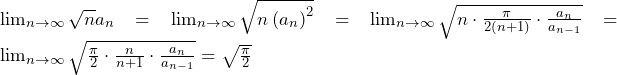 ……(答)
……(答)