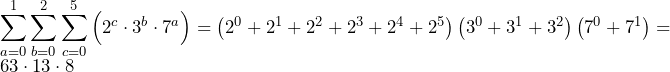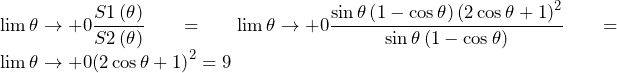慶應義塾大学過去問徹底研究 2016年 大問4 方針の立て方 (1) 実際にに小さい順から値を代入して確かめてみることで,方針どころか答えが得られる. (2) この問題の困難の一つは未知数が多いことである().まずはこの未知数を減らしたい.事実Fを用いればを消去できると考え,早速事実Fを用いる.この
- …続きを読む
-
慶應義塾大学過去問徹底研究 2016年 大問4
方針の立て方
(1)
実際に に小さい順から値を代入して確かめてみることで,方針どころか答えが得られる.
に小さい順から値を代入して確かめてみることで,方針どころか答えが得られる.(2)
この問題の困難の一つは未知数が多いことである( ).まずはこの未知数を減らしたい.事実Fを用いれば
).まずはこの未知数を減らしたい.事実Fを用いれば を消去できると考え,早速事実Fを用いる.この問題では,整数
を消去できると考え,早速事実Fを用いる.この問題では,整数 が任意であることに注意したい.また,複素数の累乗を見たらド・モアブルの定理を疑うことは基本解法としておさえておきたい.その後,
が任意であることに注意したい.また,複素数の累乗を見たらド・モアブルの定理を疑うことは基本解法としておさえておきたい.その後, を動かすことで答えが分かる.
を動かすことで答えが分かる.(3)
複素数の累乗を見たらド・モアブルの定理を疑うという基本解法,三角関数は 周期の関数であることから方針を得る.その後は,分数の厄介さを解消するために分母を払うこと,更に,
周期の関数であることから方針を得る.その後は,分数の厄介さを解消するために分母を払うこと,更に, が互いに素であることから,1次不定方程式に持ち込むことを考えたい.
が互いに素であることから,1次不定方程式に持ち込むことを考えたい.(4)
(2)と問題設定が似ているため,(2)の結果を用いたい.その後は素直に集合 の要素と集合
の要素と集合 の要素を掛け合わせたものを考えていけばよい.
の要素を掛け合わせたものを考えていけばよい. の範囲を考えれば,重複を考える必要があると分かる.
の範囲を考えれば,重複を考える必要があると分かる. と
と が互いに素でないときは,
が互いに素でないときは, (
( は互いに素な整数)と書けることは頻出の解法のためおさえておきたい.
は互いに素な整数)と書けることは頻出の解法のためおさえておきたい.解答例
(1)
ツ:3
(2)
テ:
(3)以下、解答
 (
( は整数)となる
は整数)となる が存在すれば必要十分.
が存在すれば必要十分.

 ,
, は互いに素であるから,この1次不定方程式を満たす整数の組
は互いに素であるから,この1次不定方程式を満たす整数の組 は存在する.
は存在する.
証明終了.
(4)
ト:
ナ:
解説
(1)
 は,自明に不可.
は,自明に不可.
 のとき,
のとき,
 (ド・モアブルの定理)
(ド・モアブルの定理) 
よって,求める は3……(答)
は3……(答)(2)
事実Fから,
 {
{ は整数
は整数 を用いて
を用いて と表される複素数
と表される複素数
となる.
 は,
は, のそれぞれの値に対して,異なる複素数となるが,それ以外の整数については,
のそれぞれの値に対して,異なる複素数となるが,それ以外の整数については, のどれかの整数を代入した複素数と同じ複素数となる.
のどれかの整数を代入した複素数と同じ複素数となる.
 ……(答)
……(答)(4)
(2)と同様に考えると,
 {
{ は整数
は整数 を用いて
を用いて と表される複素数}
と表される複素数}
 {
{ は整数
は整数 を用いて
を用いて と表される複素数}
と表される複素数}
であり,


である.
〇 と
と が互いに素であるとき
が互いに素であるとき

ここで, ,
, の範囲で考えると(この範囲のみで考えても,
の範囲で考えると(この範囲のみで考えても, ,
, の全ての要素を考えつくしたことになる),
の全ての要素を考えつくしたことになる), ,
, より,
より,
 ≦
≦
となる.よって, と
と の異なる要素の組を掛け合わせたとしても,その積に重複が生じる可能性があると考えられるが,以下では,その重複が存在しないことを示す.
の異なる要素の組を掛け合わせたとしても,その積に重複が生じる可能性があると考えられるが,以下では,その重複が存在しないことを示す.
そのために,
 (
( )
) 

となる整数の組 を考える.
を考える.
上の方程式を満たす の組が,
の組が, のみであることを示せれば,必要十分である.
のみであることを示せれば,必要十分である.
まず, となるには,
となるには,

が必要.
次に, となるには,
となるには,

であること( と
と は互いに素であるから,左辺は既約分数)と,
は互いに素であるから,左辺は既約分数)と, より,
より,

が必要だが, は不可.
は不可.
よって,方程式を満たす の組は存在しない.
の組は存在しない.
以上より,方程式を満たす の組は
の組は のみである.
のみである.
つまり, と
と の異なる要素の組を掛け合わせたとき,その積に重複が生じる可能性はないことが示せた.
の異なる要素の組を掛け合わせたとき,その積に重複が生じる可能性はないことが示せた.
よって,
 ……(答)
……(答)
〇 と
と が互いに素でないとき
が互いに素でないとき
 (
( は互いに素な整数)
は互いに素な整数)
と書ける.

上記の議論と比べれば,
 ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。







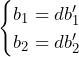 (
(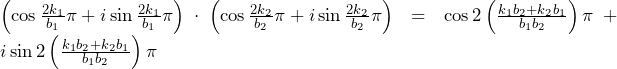

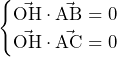
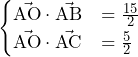
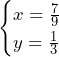
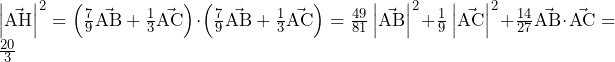

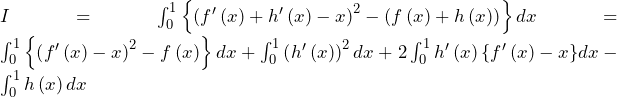
![Rendered by QuickLaTeX.com \therefore I-J=2\int_{0}^{1}{h^\prime\left(x\right)\left{f^\prime\left(x\right)-x\right}}dx-\int_{0}^{1}h\left(x\right)dx\bigm=-\int_{0}^{1}{h^\prime\left(x\right)\left(x+\frac{1}{2}\right)}dx-\int_{0}^{1}h\left(x\right)dx\ \ \ \ \ \left(\because f\left(x\right)=\frac{1}{4}x\left(x-1\right)\right)\bigm={-\left[h\left(x\right)\left(x+\frac{1}{2}\right)\right]}^1_0+\int_{0}^{1}h\left(x\right)dx\ \ -\int_{0}^{1}h\left(x\right)dx\ \ \ \ \ 第1項に部分積分 =0\ \ \ \ \ (\because h\left(0\right)=h\left(1\right)=0)](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-cdace22139508f6a5cfc0eb76395adfa_l3.png)
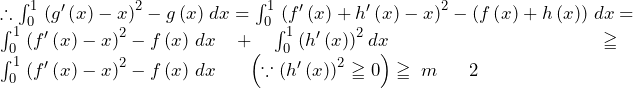
![Rendered by QuickLaTeX.com \int_{0}^{1}\left{\left(f^\prime\left(x\right)-x\right)^2-f\left(x\right)\right}dx=\int_{0}^{1}\left{\left(\left(2a-1\right)x-a\right)^2-\left(ax^2-ax\right)\right}dx\bigm=\int_{0}^{1}\left{\left(4a^2-5a+1\right)x^2-\left(4a^2-3a\right)x+a^2\right}dx\bigm=\left[\frac{4a^2-5a+1}{3}x^3-\frac{4a^2-3a}{2}x^2+a^2x\right]<em>0^1\bigm=\frac{1}{3}a^2-\frac{1}{6}a+\frac{1}{3}\bigm=\frac{1}{3}\left(a-\frac{1}{4}\right)^2+\frac{5}{16}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-4697d0443e87905f22dc8947fc187471_l3.png)