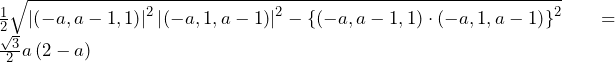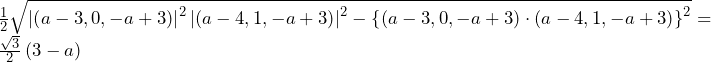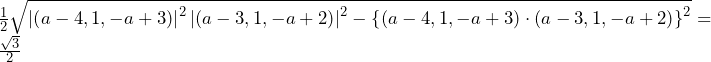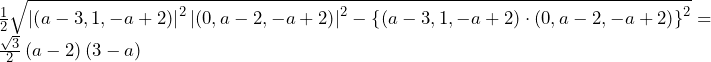方針の立て方 (1)(2)ともに,ケース1~4のどのケースが適用されるのかが直観的に分からないため,「仮にこのケースが適用されるなら」と考えて,ケース1から順番に代入していく.このような既存の分野にとらわれない新傾向の出題はSFCや商学部で多く見られるが,これら新傾向問題の攻略法は地道に片っ端から試
- …続きを読む
- 方針の立て方
(1)(2)ともに,ケース1~4のどのケースが適用されるのかが直観的に分からないため,「仮にこのケースが適用されるなら」と考えて,ケース1から順番に代入していく.このような既存の分野にとらわれない新傾向の出題はSFCや商学部で多く見られるが,これら新傾向問題の攻略法は地道に片っ端から試してみることにある.そのまま代入したり試行したりすることで答えまで至る今回のような問題もあれば,途中で規則性に気付いて解答する問題もある.どちらにせよ,分からなかったら試してみるということを心がけよう.解答例
(85)(86)(87)……060
(88)(89)(90)……180
(91)(92)(93)……150
(94)(95)(96)……200
(97)(98)(99)……035
(100)(101)(102)……035
(103)(104)(105)……050
(106)(107)(108)……140解説
(1)
〇 の範囲((85)~(90)について)
の範囲((85)~(90)について)
ケース1が適用されるなら, が必要で,
が必要で, となるには,
となるには, が必要.
が必要.
ケース2が適用されるなら, となるから,
となるから, のとき
のとき となるため,
となるため, が必要となる.
が必要となる.
ケース3が適用されるなら, となるから,
となるから, のとき
のとき となるため,
となるため, が必要となる.
が必要となる.
ケース4が適用されるなら, のとき
のとき となるため,
となるため, となるには
となるには が必要となる.
が必要となる.
以上より, ……(答)
……(答)
〇 が
が の4倍となるとき((91)~(96)について)
の4倍となるとき((91)~(96)について)
ケース1が適用されるなら, より,満たす
より,満たす は存在しない.
は存在しない.
ケース2が適用されるなら, であり,
であり, のもとで,
のもとで, より,
より, となる
となる は存在しない(
は存在しない( となり,
となり, に抵触).
に抵触).
ケース3が適用されるなら, であり,
であり, のもとで,
のもとで, より,
より, となる
となる は
は .
.
ケース4が適用されるなら, のもとで,
のもとで, より,
より, となる
となる は
は .
.
以上より, ……(答)
……(答)(2)
ケース1が適用されるなら, が必要だが,
が必要だが, も
も もこの範囲にない.
もこの範囲にない.
ケース2が適用されるなら,

が必要となる. は
は の範囲内であるから,
の範囲内であるから, とした式が成り立ち,
とした式が成り立ち,
 となる.……(答)
となる.……(答)
ケース3が適用されるなら, に対して
に対して が必要となる.
が必要となる. は
は の範囲内であるから,
の範囲内であるから, とした式が成り立ち,
とした式が成り立ち,
 ……(答)
……(答)






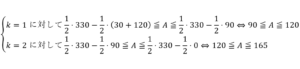
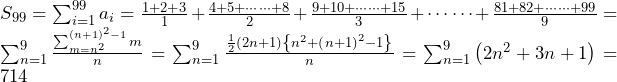 ……(答)
……(答)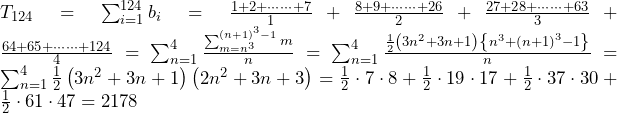 ……(答)
……(答)
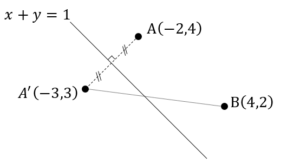
![Rendered by QuickLaTeX.com \int_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}\left(q-x^2\right)dx=\int_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}\left\{\left(r+\frac{1}{2}\right)^2-x^2\right\}dx=\left[\left(r+\frac{1}{2}\right)^2x-\frac{1}{3}x^3\right]_{-\left(r+\frac{1}{2}\right)}^{r+\frac{1}{2}}=\frac{4}{3}r^3+2r^2+r+\frac{1}{6}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-94aeca5089102bd3c6cc95fc6a86c7e9_l3.png) ……(答)
……(答)