物理 | 【早慶専門対策】個別指導塾ヒロアカ

【物理】力学的エネルギー保存則(仕事・エネルギーその3)

2017.02.11

力学的エネルギー保存則とは（運動エネルギー）＋（重力による位置エネルギー）＋（弾性エネルギー）＝（一定）という式で表される法則で、力学的エネルギーの総和は保存されるということを表しています。例えば、高さｈから物体が自由落下したとします。このとき、落下前の位置エネルギーはmgh、地面に到達した

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]力学的エネルギー保存則ってとても便利な法則だね。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]最初のエネルギーからその後の物体の速さとか求められるようになるしね！[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]そうそう！けど、成り立たない場合もあるらしいから注意しなきゃ。[/speech_bubble]
力学的エネルギー保存則とは

（運動エネルギー）＋（重力による位置エネルギー）＋（弾性エネルギー）＝（一定）

という式で表される法則で、力学的エネルギーの総和は保存されるということを表しています。

例えば、高さｈから物体が自由落下したとします。

このとき、落下前の位置エネルギーはmgh、地面に到達したときの運動エネルギーは $\frac{1}{2}mv^{2}$ となり、位置エネルギーが運動エネルギーへと変化します。

力学的エネルギー保存則より、mgh＝ $\frac{1}{2}mv^{2}$ となり、ここから速さvを求めることが可能になります。

しかし、摩擦力や、手で力を加えるなどの外力が働いたときにはこの法則は成り立たないので注意しましょう。

摩擦力などの抵抗力が働くと、エネルギーは熱となって外へでていってしまいます。

これは非常に多くの問題で使用する法則なのでしっかりと覚えましょう。

【物理】運動量保存則と具体例(運動量・力積その3)

2017.01.14

衝突前の速度から、衝突後の速度を求める問題は、運動量保存則というものを使って解くことができます。これは、「作用・反作用の力のみがはたらく物体の運動量の和は一定である」という法則です。まずは式でこの法則を導いてみましょう。運動量保存則の導き方質量がそれぞれの物体1,2が、それぞれ速度 (図右向きを

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]物体が衝突した後の速度って、どうしたら求められるんだろう。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]物体にはたらいた力が分からないから、よくわからないね。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]衝突した時間が分からないから、力積もわからないよね。[/speech_bubble]
衝突前の速度から、衝突後の速度を求める問題は、運動量保存則というものを使って解くことができます。これは、「作用・反作用の力のみがはたらく物体の運動量の和は一定である」という法則です。まずは式でこの法則を導いてみましょう。

運動量保存則の導き方

質量がそれぞれ $m_{1},m_{2}$ の物体1,2が、それぞれ速度 $v_{1},v_{2}$ (図右向きを正とする)で運動しているとします。この物体が衝突した後、それぞれの速度が $v'_{1},v'_{2}$ になったとします。

物体1,2のみを考えると、この2つの物体には衝突後の作用・反作用の力のみはたらいています。
図は右向きが正となっているので、物体1にはたらく力を-F、物体2にはたらく力をFとします。

また、衝突してから離れるまでにかかった時間をtとします。
物体にはたらく力、および力がはたらく時間をおいたので、運動量と力積の式を立ててみます。物体1、2それぞれについての運動量と力積の式は

$-Ft=m_{1}v'_{1}-m_{1}v_{1}$

$Ft=m_{2}v'_{2}-m_{2}v_{2}$

のようになります。この2式の辺々を足し合わせて整理すると

$m_{1}v_{1}+m_{2}v_{2}=m_{1}v'_{1}+m_{2}v'_{2}$

のような等式が得られます。この式こそ、作用・反作用のみがはたらく物体の運動量の和が一定である、という運動量保存則の式なのです。

この式は、力学的エネルギー保存則と似ていますが、適用できる条件が異なります。

力学的エネルギー保存則は「摩擦や空気抵抗などで失われるエネルギーがない場合」、運動量保存則は「作用・反作用のみがはたらく場合」に適用できます。

例えば「重力に引かれて落下する物体」を考えると、空気抵抗を考慮しない場合は位置エネルギーが運動エネルギーに変化しているので力学的エネルギー保存則は成り立ちます。

ですが、作用・反作用以外の力がはたらいている(物体が地球を引く力は考慮していないため)ので、運動量保存則は成り立ちません。

また、少し先の単元になりますが、「2つの物体が非弾性衝突した場合」を考えると、エネルギーが失われてしまうため力学的エネルギー保存則は成り立ちません。
ですが、作用・反作用の力のみがはたらいているため運動量保存則は成り立ちます。

衝突後の物体の速度を求める

速度4.0m/sで運動する質量3.0kgの小球Xと、速度-2.0m/sで運動する質量2.0kgの小球Yが衝突しました。
衝突後、小球Yの速度は2.5m/sでした。このとき、衝突後の小球Xの速度vを求めよ。

物体同士の衝突では、作用･反作用の力のみがはたらきますので、運動量保存則を適用することができます。

運動量保存則の式を立ててみましょう。

3.0×4.0+(-2.0)×2.0=3.0×v+2.5×2.0

この式を整理すると、速度v=1.0m/sとなります。

【物理】みんな困る！　等速円運動ってどう理解する（円運動その１）

2017.01.13

等速円運動は、イメージがしづらいためか苦手な人の多い分野です。ですがひとつづつ理解していけば、必ずできるようになるので、一つずつ内容を理解して下さい。等速円運動の特徴とは？等速円運動の特徴としては ①物体が円軌道をえがく ②中心力が働き、加速度は円軌道の中心に働くです。まず①から見ていきましょ

…続きを読む
等速円運動は、イメージがしづらいためか苦手な人の多い分野です。ですがひとつづつ理解していけば、必ずできるようになるので、一つずつ内容を理解して下さい。 [toc]
等速円運動の特徴とは？

等速円運動の特徴としては

①物体が円軌道をえがく

②中心力が働き、加速度は円軌道の中心に働く

です。まず①から見ていきましょう。

この運動の特徴としてまず“等速“とあるので”速さ”は同じですが“速度”は時々刻々と変化します。
そして速度は円の接線方向を向きます。

これはハンマー投げを想像するとなんとなくわかるのではないでしょうか？

詳細な証明はこの段階では理解が難しいので省きます。まずはイメージしましょう。

図1を見てください。

図１

速度が違うのは物体の速さが同じでも向きが違うためです。
ここで力学の関係から以下のことがわかります。

速度変化がある→加速度が生じている→力が働いている

では、この力はどこに働いているのかを二通りで説明します

(i)まず力の向きは円軌道の中心に働いています。
これもハンマー投げで考えてみましょう。
体を回転させると手とハンマーが糸の張力によってピーンと張ります。
この張力ここでの力です。
そして物体に働く力と加速度の方向は同じ方向を向くということから加速度も中心に働くことがわかります。

(ii)速度変化を調べることからもわかります。図2を見てください。

図２

速度が時間秒後にに変化したとします。加速度は

$\vec{a} = \frac{\vec{v^{'}}- \vec{v} }{ \Delta t }$

となります。これは図２の赤い矢印に対応しています。
このΔtを小さくしていく（図2の右側の図の青い点線の矢印に対応）と赤い矢印がどんどん水平になっていくことがわかります。

加速度はΔt→0を考えることなので、加速度は円の中心に働くことがわかります。
よって加速度の向きと力の方向は一緒なので、円軌道の中心に働くことがわかります。

以上②を(i),(ii)と二通りの説明をしました。

(i)は直感的な説明なのでまず物理の苦手な人はこのことから理解できたらと思います。

最終的にはどちらでも理解できるようになりましょう。

【物理】エネルギー(仕事・エネルギーその2)

2017.01.07

エネルギーとはエネルギーとは、どれだけ仕事をできるかを表しています。その単位は仕事と同じくJ（ジュール）です。エネルギーは大きく、運動エネルギーと位置エネルギーに分類されます。さらに位置エネルギーはバネによる弾性エネルギー、物体の高さによる重力による位置エネルギーなどに分けられます。運動エ

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]仕事はわかったけど、エネルギーとどう違うの？単位も同じだし違いがわからない。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]エネルギーはどれだけ仕事をできるか、だから似たようで違うものだね。つまり仕事をするということは相手にエネルギーを与えることだよ。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]なるほど！[/speech_bubble]
エネルギーとは

エネルギーとは、どれだけ仕事をできるかを表しています。
その単位は仕事と同じくJ（ジュール）です。

エネルギーは大きく、運動エネルギーと位置エネルギーに分類されます。

さらに位置エネルギーはバネによる弾性エネルギー、物体の高さによる重力による位置エネルギーなどに分けられます。

運動エネルギー

まず、運動エネルギーとは運動している物体がもつエネルギーのことで、

質量m、速さv、で運動している物体の運動エネルギーは

$\frac{1}{2}mv^{2}$

で表されます。

重力による位置エネルギー

これは高さによるエネルギーです。高さｈにある質量ｍの物体のエネルギーはｍｇｈで表されます。
ここで基準となる高さは自分で決定してよいので、わかりやすい高さを０にするようにしましょう。

弾性エネルギー

これはバネによるエネルギーです。

自然長の位置を基準として、どれだけ変化したかをｘ，バネ定数をkとすると、

$\frac{1}{2}kx^{2}$ で表されます。

仕事とエネルギー

さらに、仕事とエネルギーの関係は以下の式であらわせます。

（物体の運動エネルギーの変化）＝（物体に力がした仕事）

例えば、速さｖで動いていた物体に力Fを加えた時、物体の速度がｖ’に変化したとします。

このとき、動かした距離をxとすると、

物体の運動エネルギーの変化　＝　 $\frac{1}{2}mv'^{2} - \frac{1}{2}mv^{2}$

物体に力がした仕事　＝　Fx　であり、

$\frac{1}{2}mv'^{2} - \frac{1}{2}mv^{2}$ 　＝　Fx　が成り立ちます。

【物理】運動量と力積の関係の具体例(運動量・力積その2)

2017.01.07

前記事で運動量と力積の関係について示しましたが、具体例を挙げて考えてみましょう。物体を止める力の大きさまず例題を考えてみます。 (例題)質量30 kgの物体が右向きに速さ10 m/sで運動している。この物体に左向きに一定の力Fを6秒間加えると、物体は静止した。このとき、物体に加えた力F[N]を求

…続きを読む
前記事で運動量と力積の関係について示しましたが、具体例を挙げて考えてみましょう。

物体を止める力の大きさ

まず例題を考えてみます。

(例題)質量30 kgの物体が右向きに速さ10 m/sで運動している。この物体に左向きに一定の力Fを6秒間加えると、物体は静止した。このとき、物体に加えた力F[N]を求めよ。

左向きの力Fを正とすると、物体が最初に運動していた向きは右向きであるので、負となります。よって、力を加える前の物体の運動量は

30×(-10)=-300[kg・m/s]

となります。よって、運動量と力積の関係式は

0-(-300)=F×6

となります。ここで、左辺は運動量の変化量、右辺は力積となります。この式より、物体にはたらいていた力FはF=50[N]となります。

この問題では一定の力Fはどのような力か決められていませんでした。ですが、例えば動摩擦力は一定の力ですので、動摩擦力について考える場合はこの問題のように力積を用いて考えることができます。物体が止まるまでの時間が示されている時に物体にはたらいている動摩擦力を求めたり、逆に動摩擦係数が分かっている時、動摩擦力から止まるまでの時間を求めたり、といった問題を解けるようになります。

壁で跳ね返った球

質量m、速度 $v_{0}$ の球が壁で跳ね返り、速さが逆向きでvになったとします。このとき球が受けた力積を考えてみましょう。

球にはたらいた力も時間も与えられていないので、直接力積を求めることはできません。
この場合、運動量の変化を求めることで力積を間接的に求めることができます。

球が受けた力積は、図で左向きの方向です。

ですので、左向きを正として考えます。

球が壁で跳ね返る前、球は右向きに運動しているので、運動量は $-mv_{0}$ です。
壁で跳ね返った後、球は左向きに運動しているので、運動量はmvです。よって、力積は

$mv-(-mv_{0})=m(v+v_{0})$

のように求められます。

前の問題のように力積を先に求めることもありますが、この問題のように運動量の変化から力積を間接的に求める問題もあります。

自由に使い分けられるようにしましょう。

【物理】運動量と力積とは？(運動量・力積その1)

2017.01.06

運動量と力積については、少しつかみどころがない分野なので、分かりにくい印象を持つ人も多いと思います。ですが、運動方程式や力学的エネルギーと同様に、物体の運動の考え方の1つですので、先にそれらを学んでおけばすんなりと頭に入ってくると思います。例えば、2つの球が衝突するという状況を考えてみます。このと

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]運動量と力積って聞いたことあるけど、そもそも何なんだろう。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]運動量は「質量×速度」、力積は「力×時間」で表されるみたいね。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]全然違う量みたいだけど、何か関係があるのかな。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]運動量の変化を力積で表すことができるんだって。[/speech_bubble]
運動量と力積については、少しつかみどころがない分野なので、分かりにくい印象を持つ人も多いと思います。ですが、運動方程式や力学的エネルギーと同様に、物体の運動の考え方の1つですので、先にそれらを学んでおけばすんなりと頭に入ってくると思います。

例えば、2つの球が衝突するという状況を考えてみます。このとき、運動量と力積を使えば、物体にはたらいた力や物体の加速度を求めなくとも、衝突後の2つの球の速度を求めることができます。今まで運動方程式やエネルギーを用いて考えていた問題についても、運動量と力積の関係を使えばより簡単な式で解ける場合もあるため、重要な考え方となります。

運動量と力積とは

運動量は運動の激しさを表す量で、質量と速度の積で表されます。質量mの物体が速度vで動いている場合、運動量PはP=mvとなります。

同じ速度であれば、質量が重い方が運動量が大きくなります。人間と車が同じ速度で運動している場合、車の方が運動量が大きくなります。また、同じ質量であれば、速度が大きい方が運動量が大きくなります。

力積は、力と、その力がはたらいた時間の積で表されます。物体に力Fがt秒加わっていた場合、力積IはI=Ftとなります。

運動量と力積の関係

質量mの物体に、一定の力Fがt秒間はたらき、速度がvからv’に変化したとします。

このとき、この物体にかかる加速度aは $a=\frac{(v^{'}-v)}{t}$ となります。よって、物体の運動方程式は

$F=\frac{m(v^{'}-v)}{t}$

となります。

この運動方程式を変形すると、Ft=mv’–mvという等式が得られます。この等式の左辺は力積、右辺は運動量の変化量です。つまりこの式は、「力積＝運動量の変化量」という関係を表しています。

「運動量と力積は違う物理量なのに等式として扱っていいのか？」と思うかもしれません。ですので、運動量と力積の単位について考えてみます。運動量は質量[kg]と速度[m/s]の積ですので、単位は[kg・m/s]となります。また、力積は力[kg・m/ s $^{2}]$ と時間[s]の積ですので、単位は[kg・m/s]となります。よって、運動量と力積の単位は同じとなるので、等式の上で扱っても大丈夫ということになります。

【物理】運動方程式の例(運動方程式その3)

2016.12.21

運動方程式の例運動方程式の立て方を具体例を用いて説明します。まず、物体を手で引っ張った場合を考えます。質量ｍの物体を大きさFの力で引っ張ったとします。この場合は右向きを正にとると、F＝maとなり、この物体は加速度a=F/mという一定の加速度で右向きに加速していくことがわかります。 &nbsp

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]よーし、理解したから次は実際の問題をやってみるね！[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]簡単な問題は大丈夫だけど、斜面の問題とかわからなくなっちゃう。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]しっかりとｘ軸、ｙ軸に力をわけて考えると、そんなに難しくないよ。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]ありがとう、やってみる！[/speech_bubble]
運動方程式の例

運動方程式の立て方を具体例を用いて説明します。

まず、物体を手で引っ張った場合を考えます。

質量ｍの物体を大きさFの力で引っ張ったとします。

この場合は右向きを正にとると、F＝maとなり、この物体は加速度a=F/mという一定の加速度で右向きに加速していくことがわかります。

次に、斜面を運動する物体を考えます。

まず、加速度aの向きから、図のようにX軸、Y軸を設定します。

ちからをすべて図示すると、運動方程式が２つ書けます。

ｘ軸方向：ma=mgsinθ

ｙ軸方向：m×0=N–mgcosθ

ｙ軸については静止しているため加速度がゼロになっています。つまり力の釣り合いとは運動方程式において物体が静止しているときとも考えることができます。

ここから、a=gsinθ、N=mgcosθが求まります。

最後に複数の物体についての運動方程式です。

複数の物体を考えるときはそれぞれについて運動方程式を立てると考えやすいです。今回は左右の物体それぞれについて考えてみましょう。

左側の物体：Ma＝F–ｆ・・・①

右側の物体：ma＝ｆ・・・②

となります。ここで①＋②を考えてみると

(M+m)a＝F・・・③

となります。

ここで、③の赤い字のところを考えると、２つの物体を一体化して考えていることと同じであるということがわかります。今回出てきたｆは内力と呼ばれ、作用・反作用の法則に物体を一体化して考えると消えます。

【物理】運動方程式の立て方(運動方程式その2)

2016.12.21

運動方程式の立て方運動方程式はma=Fで表されます。まず、このｍはどの物体についてなのか、注目する物体を決めます。この質量がｍになります。次に、加速する方向を見極めます。このとき、加速度aと同じ方向にｘ軸、垂直な方向にｙ軸をとるとわかりやすいです。最後に、この物体について働く力をすべて図示し

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]運動方程式は何だかはわかったけど実際どうやって使うの？[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]とりあえず力を全部図示してみればいいのかな？[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]ん−。ｘ軸、ｙ軸はどうやってとったらいいのかとか難しいね。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]そもそもつりあっているところも運動方程式を立てられるの？[/speech_bubble]
運動方程式の立て方

運動方程式はma=Fで表されます。

まず、このｍはどの物体についてなのか、注目する物体を決めます。この質量がｍになります。

次に、加速する方向を見極めます。このとき、加速度aと同じ方向にｘ軸、垂直な方向にｙ軸をとるとわかりやすいです。

最後に、この物体について働く力をすべて図示します。こうして、x軸、y軸に力を分解し、それぞれについて運動方程式を立てることができます。

つりあっている物体についても運動方程式は立てることができます。このときは、a=0になるので、左辺は０になるだけです。

【物理】運動方程式とは？(運動方程式その1)

2016.12.15

運動方程式は、力学において最も重要な関係式の1つです。なんとなく学んでいるとつまずきやすいポイントですので、しっかり理解しておきましょう。運動方程式とは例として、平面上で台車(＝摩擦力を考えない物体)に力Fが加わって走っている場合を考えます。この場合、運動方程式は、下のような式で表されます。

…続きを読む
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]運動方程式について習ったけど、よく分からないなぁ。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]力が加わると物体が加速する、っていう意味らしいよ。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]動いている物体には力がはたらいているってこと？[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]動いている物体じゃなくて、加速している物体みたいだけど、ちょっと難しいよね。[/speech_bubble]
運動方程式は、力学において最も重要な関係式の1つです。なんとなく学んでいるとつまずきやすいポイントですので、しっかり理解しておきましょう。

運動方程式とは

例として、平面上で台車(＝摩擦力を考えない物体)に力Fが加わって走っている場合を考えます。

この場合、運動方程式は、下のような式で表されます。

F=ma

ここで、mは物体の質量、aは物体の加速度です。力と加速度の向きは一致します。

運動方程式はF=maで表され、質量mの物体に力Fがはたらくとき、その物体は加速度aで運動する、という意味の方程式です。

他の例として、重力を考えてみます。重力加速度をgとしたとき、質量mの物体に働く重力はmgです。力のつり合いを考える上で、平面の上で止まっている物体にはたらく重力と物体に対する抗力を考えたと思いますが、その際物体にはたらく重力はmgとなります。もし物体が何にも接していないと、抗力が働かないため、物体は加速度gで鉛直下方向に落下します。

また、加速度をもたない(a=0)の物体の場合、物体にはたらく力の合力は0となります。加速度をもたない物体は、静止または等速直線運動をしています。よって、力がつり合っている場合は、運動方程式において=0の場合と考えることができます。

注意しておきたいこととして、「物体が動いているときは物体に力がはたらいている」ではありません。上の図では、平面上を等速で台車が走っている状態を表していますが、この台車は等速なので加速度は0であり、力は働いていません(現実には空気抵抗があるので力は働いていますが)。

【物理】剛体のつり合いと重心(力のモーメントその2)

2016.12.15

剛体が静止しているとき、運動も回転もしていません。よって、剛体にはたらく力のつり合いだけではなく、力のモーメントもつり合っている必要があります。モーメントとは、剛体を回転させる力です。力のモーメントがつり合っているとき、時計回りのモーメントと反時計回りのモーメントの大きさが等しくなっています。 2

…続きを読む
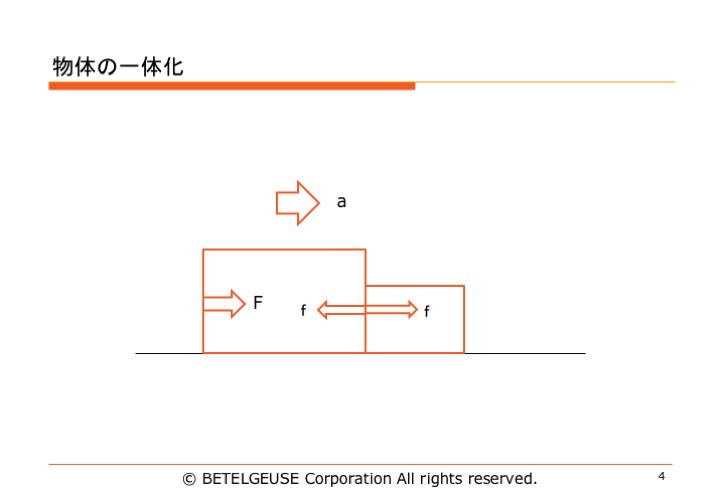
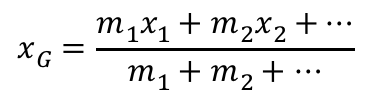[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]物体にはたらく力がつり合っていれば、物体は動かないんだったよね。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]大きさのある物体(剛体)について考える時は、力のモーメントもつり合ってないといけないよ。[/speech_bubble] [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]そうか、力のモーメントがつり合っていないと剛体は動いちゃうんだよね。[/speech_bubble] [speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]力のモーメントのつり合いについて考えるときは、重心についても考えないといけないね。[/speech_bubble]
剛体が静止しているとき、運動も回転もしていません。よって、剛体にはたらく力のつり合いだけではなく、力のモーメントもつり合っている必要があります。

モーメントとは、剛体を回転させる力です。力のモーメントがつり合っているとき、時計回りのモーメントと反時計回りのモーメントの大きさが等しくなっています。

2つのおもりがつり合っている場合

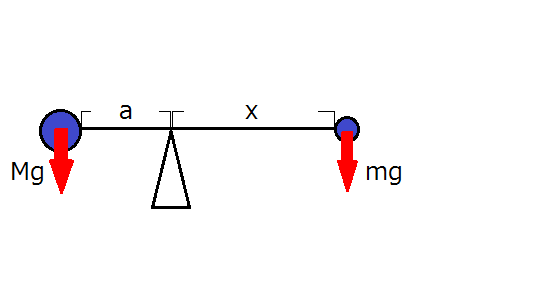
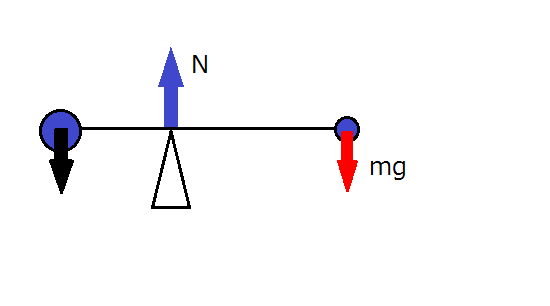
左右におもりがついた棒が支柱に支えられて静止している状態を考えます。左側のおもりの質量をM、右側のおもりの質量をmとします。棒の質量は考えません。また、支柱から棒の左端までの長さをa、右端までの長さをxとします。このとき、xを求めてみます。

支柱を支点としたとき、右のおもりにはたらく重力によって、棒は時計回りに回転しようとします。また、左のおもりにはたらく重力によって、棒は反時計回りに回転しようとします。この2種類のモーメントがつり合っているので、

mgx=Mga

が成り立ちます。よって、 $x=\frac{Ma}{m}$ となります。

この例では支柱がある位置を支点としました。しかし、モーメントがつり合っている場合はどの地点を支点としてもいいのです。モーメントがつり合っているということは剛体が回転していないので、どこを支点をしてもモーメントはつり合っているのです。

左のおもりを支点として考えます。このとき、右のおもりにはたらく重力により棒は時計回りに回転しようとします。
また、支柱にはたらく抗力Nにより棒は反時計回りに回転しようとします。左のおもりにはたらく重力については、支点からの距離が0なので無視できます。よって、

mg(a+x)=Na

が成り立ちます。ここで、力のつり合いによりN=(m+M)gであるので、

mga+mgx=mga+Mga

が成り立ち、先程と同様に $x=\frac{Ma}{m}$ が求められました。

結果は同じでしたが、この例では支柱を支点とした場合の方が計算が楽になりました。どの点を支点をした場合でも問題を解くことはできますが、多くの力がはたらいている点、および求めるのに手間がかかる力がはたらいている点を支点として考えた方が計算が楽な場合が多いです。

重心について考える

先程の問題では、棒の質量を無視することができました。しかし、棒の質量が無視できない場合もあります。このような場合、剛体のどの部分に重力がはたらいているか分からなければモーメントを求めることができません。このようなとき、剛体の一点に力がはたらいているものと考え、その点を重心と呼びます。

物体を構成する質点の質量を $m_{1},m_{2}･･･$ とし、座標を $(x_{1},y_{1}),(x_{2},y_{2})･･･$ とします。このとき、重心の質量を $x_{G}$ とすると

のようになります。y座標に関しても同様に求められます。

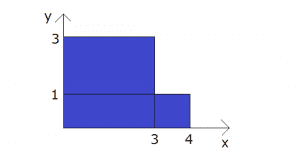
球や直方体の箱のように、対称な物体の場合、重心はその剛体の中心になります。では、不規則な物体についてはどのように求めればいいでしょうか。例として、以下のような物体の重心を求めてみます。

重心の求め方は、基本的には

①物体を分かりやすい形に分割する

②分割した図形の重心と質量を求める

③各重心、各質量を上記の式に代入する

といった手順で求められます。この手順に従って求めてみましょう。

まず、物体を分かりやすい形に分割します。この場合、3×3の正方形と1×1の正方形に分割できます。

次に、それぞれの図形の重心と質量を求めます。3×3の正方形と1×1の正方形の重心は、それぞれ(1.5,1.5),(3.5,0.5)となります。1×1の正方形の質量をmとすると、3×3の正方形の質量は9mとなります。

したがって、求める重心の座標は

$x_{G}$ =(1.5×9m+3.5×m)/(9m+m)=1.7

$y_{G}$ =(1.5×9m+0.5×m)/(9m+m)=1.4

より、(1.7,1.4)となります。

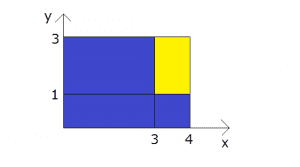
また、物体を4×3、質量12mの長方形と、1×2、質量-2mの長方形に分割する、という考え方もできます。この場合、それぞれの重心は(2,1.5),(3.5,2)となるので、

$x_{G}$ =(2×12m+3.5×(-2m))/(12m-2m)=1.7

$y_{G}$ =(3.5×12m+3×(-2m))/(12m-2m)=1.4

より、同様に(1.7,1.4)となります。