方針の立て方 問題設定がやや奇天烈だか,題意を満たす関数を考えれば良く,それ以外は極めて平易な確率の問題である. (1)~(3)の前半((12)~(26))までは,特筆事項なし. (3)の後半((27)~(30))は,題意を満たす関数の特定がやや難しい.全ての関数の組み合わせに関して「を満たすすべて
- …続きを読む
-
方針の立て方
問題設定がやや奇天烈だか,題意を満たす関数を考えれば良く,それ以外は極めて平易な確率の問題である.
(1)~(3)の前半((12)~(26))までは,特筆事項なし.
(3)の後半((27)~(30))は,題意を満たす関数の特定がやや難しい.全ての関数の組み合わせに関して「 を満たすすべての実数
を満たすすべての実数 に対して
に対して となるか」を調べるのはパターン数も多くとても面倒である.そこで,「必要条件で可能性を絞って,虱潰しする」という方法を取ろう.この考え方はよく使う手段であるから,おさえておこう.具体的には,「
となるか」を調べるのはパターン数も多くとても面倒である.そこで,「必要条件で可能性を絞って,虱潰しする」という方法を取ろう.この考え方はよく使う手段であるから,おさえておこう.具体的には,「 を満たすすべての実数
を満たすすべての実数 に対して
に対して となる」の必要条件「
となる」の必要条件「 かつ
かつ となる」を用いて,題意を満たす関数の組み合わせを絞っていく.「
となる」を用いて,題意を満たす関数の組み合わせを絞っていく.「 かつ
かつ となる」というのは,(3)の前半((22)~(26))で考えているから,すぐに
となる」というのは,(3)の前半((22)~(26))で考えているから,すぐに と分かる.後は,
と分かる.後は, と,
と, の2つを虱潰しに調べればよい.
の2つを虱潰しに調べればよい.解答例
(12)(13)

(14)(15)(16)
(17)(18)(19)(20)(21)
(22)(23)(24)(25)(26)
(27)(28)(29)(30)
解説
(1)
〇 となる確率((12)と(13)について)
となる確率((12)と(13)について)

であるから, を満たすには,
を満たすには, または,
または, であれば必要十分.
であれば必要十分.
よって, となる確率は,
となる確率は,
 ……(答)
……(答)
〇条件つき確率((14)~(16)について)
![Rendered by QuickLaTeX.com \int_{0}^{2}\left(-6x+15\right)dx=\left[-3x^2+15x\right]_0^2=18,\int_{0}^{2}\left(-3x^2+12\right)dx=\left[-x^3+12x\right]_0^2=16](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmgAAAA4AQAAAABhhTk6AAAAAnRSTlMAAHaTzTgAAAAaSURBVFjD7cEBAQAAAIIg/69uSEABAAAAfBkREAABcmKxnAAAAABJRU5ErkJggg==)
であるから, かつ
かつ となるのは,
となるのは, のとき.
のとき.
 かつ
かつ となる確率は,
となる確率は, .
.
よって,求める条件つき確率は,
 ……(答)
……(答)(2)


であるから, かつ
かつ となるような,
となるような, の組み合わせは,
の組み合わせは, の2通り.
の2通り.
よって,求める確率は,
 ……(答)
……(答)(3)
〇 かつ
かつ となる確率((22)~(26)について)
となる確率((22)~(26)について)
前問と同様に, かつ
かつ となるのは
となるのは の2通り.
の2通り.
よって,求める確率は,
 ……(答)
……(答)
〇 を満たすすべての実数
を満たすすべての実数 に対して
に対して となる確率((27)~(30)について)
となる確率((27)~(30)について)
 を満たすすべての実数
を満たすすべての実数 に対して
に対して となる関数の組
となる関数の組 を考える.
を考える.
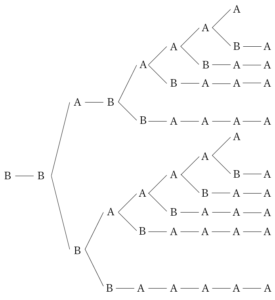
まず, で満たす必要がある(つまり,
で満たす必要がある(つまり, かつ
かつ となる必要がある)ため,考えられる組は,
となる必要がある)ため,考えられる組は, の高々2通り.
の高々2通り.
ここで,

であり,全ての実数 に対して
に対して であるから,
であるから, は題意を満たす.
は題意を満たす.
一方で
 であり,
であり, は
は で
で となってしまうから,
となってしまうから, は題意を満たさない.
は題意を満たさない.
よって,求める確率は, となる確率と等しく,
となる確率と等しく,
 ……(答)
……(答)







![Rendered by QuickLaTeX.com \int_{0}^{2}\left(-6x+15\right)dx=\left[-3x^2+15x\right]_0^2=18,\int_{0}^{2}\left(-3x^2+12\right)dx=\left[-x^3+12x\right]_0^2=16](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-c3bfa33edb30774157f6fafbfffed269_l3.png)
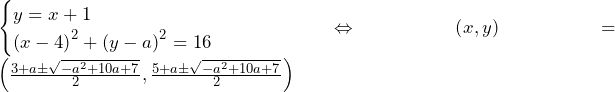 (複号同順)
(複号同順)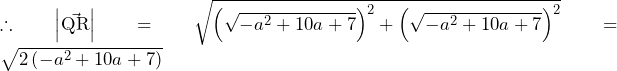
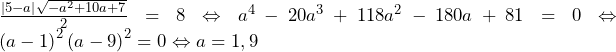 ……(答)
……(答)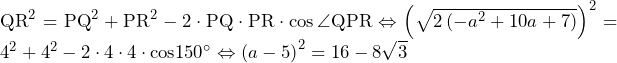 ……(答)
……(答)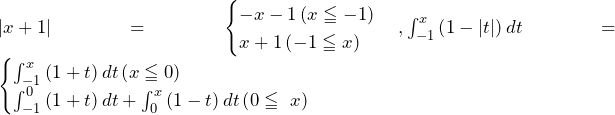 となる.
となる.![Rendered by QuickLaTeX.com F\left(x\right)=x+1+\int_{-1}^{0}\left(1+t\right)dt+\int_{0}^{x}\left(1-t\right)dt=x+1+\left[t+\frac{1}{2}t^2\right]_{-1}^0+\left[t-\frac{1}{2}t^2\right]_0^x=-\frac{1}{2}x^2+2x+\frac{3}{2}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-41c71a6f673b63fa745fc3d548c4ed52_l3.png)
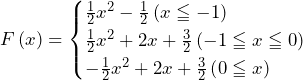 ……(答)
……(答)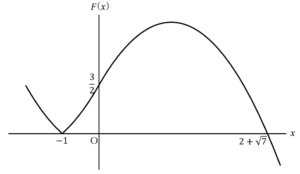
![Rendered by QuickLaTeX.com \int_{-1}^{0}\left(\frac{1}{2}x^2+2x+\frac{3}{2}\right)dx+\int_{0}^{2+\sqrt7}\left(-\frac{1}{2}x^2+2x+\frac{3}{2}\right)dx=\left[\frac{1}{6}x^3+x^2+\frac{3}{2}x\right]_{-1}^0+\left[-\frac{1}{6}x^3+x^2+\frac{3}{2}x\right]_0^{2+\sqrt7}=\frac{19+7\sqrt7}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-49c0c64db15f48db2771431bf99b4c3e_l3.png) ……(答)
……(答)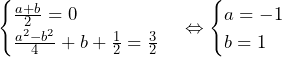
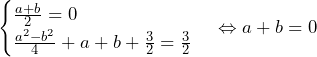
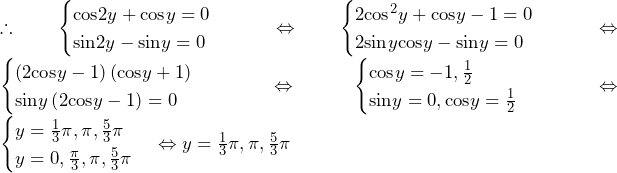 ……(答)
……(答)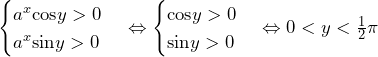
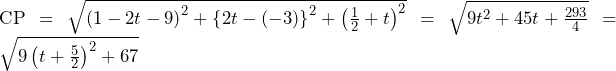
 ……(答)
……(答)
![Rendered by QuickLaTeX.com A=\int_{0}^{2}f\left(t\right)dt=\int_{0}^{2}\left(\frac{3}{a}t^2-\frac{1}{a}t+A^2\right)dt=\left[\frac{1}{a}t^3-\frac{1}{2a}t^2+A^2t\right]_0^2=2A^2+\frac{6}{a}\Leftrightarrow2A^2-A+\frac{6}{a}=0](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-ab0bf548b4a46975e7979ac67d04290f_l3.png)
![Rendered by QuickLaTeX.com \int_{0}^{b}\left\{f\left(x\right)-f\left(b\right)\right\}dx=\int_{0}^{b}\left\{\frac{3}{a}x^2-\frac{1}{a}x-\frac{3}{a}b^2+\frac{1}{a}b\right\}dx=\left[\frac{1}{a}x^3-\frac{1}{2a}x^2-\frac{3}{a}b^2x+\frac{1}{a}bx\right]_0^b=-\frac{b^2\left(4b-1\right)}{2a}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a1ae218f005a4a94ff3accbf2e2f76ee_l3.png)
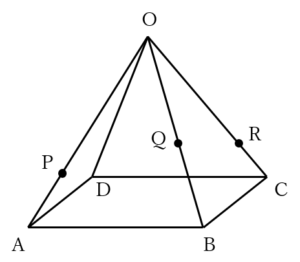
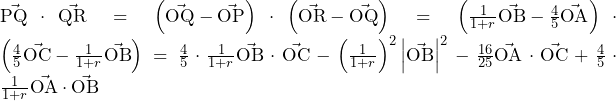
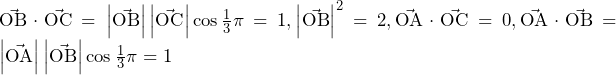 であるから,
であるから,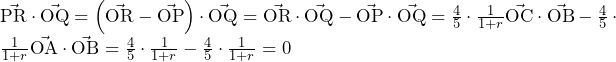 ……(答)
……(答)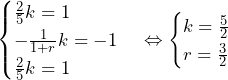
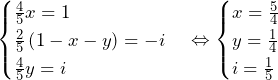
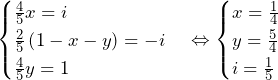
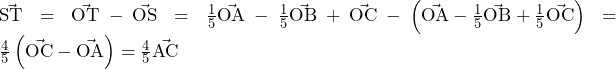
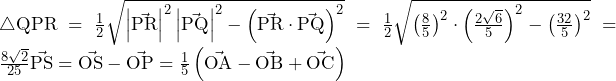 より,
より,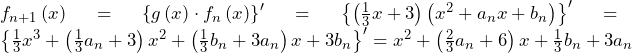
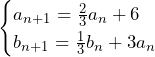 ……(答)
……(答)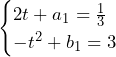
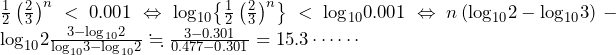
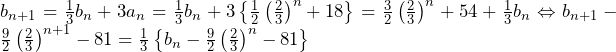
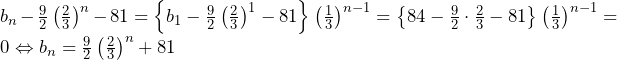 ……(答)
……(答)