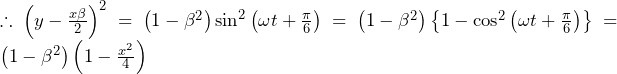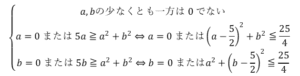2017年慶應大学理工|過去問徹底研究 大問3 方針の立て方 (1) いきなり範囲を考えると難しいため,まず範囲の制約を無視したを解く.その後で範囲を考える. (2) 実際に積分の計算を実行しなければならないが,の具体的な積分計算はできないため,何とかしての積分を解消する必要がある.そこで, で積分
- …続きを読む
-
2017年慶應大学理工|過去問徹底研究 大問3
方針の立て方
(1)
いきなり範囲を考えると難しいため,まず範囲の制約を無視した を解く.その後で範囲を考える.
を解く.その後で範囲を考える.(2)
実際に積分の計算を実行しなければならないが, の具体的な積分計算はできないため,何とかして
の具体的な積分計算はできないため,何とかして の積分を解消する必要がある.そこで,
の積分を解消する必要がある.そこで,
 で積分可能な関数
で積分可能な関数 と
と に対して,
に対して, で
で が成り立つならば,
が成り立つならば,
![Rendered by QuickLaTeX.com \left\{\min_{\left[a,b\right]}{f\left(x\right)}\right\}\int_{a}^{b}g\left(x\right)dx\leqq\int_{a}^{b}f\left(x\right)g\left(x\right)dx\leqq\left\{\max_{\left[a,b\right]}{f\left(x\right)}\right\}\int_{a}^{b}g\left(x\right)dx](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAlgAAAAcAQAAAACVS/wiAAAAAnRSTlMAAHaTzTgAAAAYSURBVBgZYxgFo2AUjIJRMApGwSigEAAACFAAAUWsvJcAAAAASUVORK5CYII=)
が成り立つことを利用する.この不等式は重要な不等式のためおさえておくこと.(3)
(F1)と(F2)が不等式であることから,はさみうちの原理を用いると考える.そのためにはまず を
を で表す必要がある.
で表す必要がある. であることから,積分区間を細かくちぎっていくという変形が思いつく.
であることから,積分区間を細かくちぎっていくという変形が思いつく.(4)
 の絶対値記号を外すために,
の絶対値記号を外すために, の符号の変わり目で場合分け(積分区間をちぎる)をする.すると前問と同じ解法に帰着する.
の符号の変わり目で場合分け(積分区間をちぎる)をする.すると前問と同じ解法に帰着する.解答例
(1)
テ:
ト:
(2)
 が偶数のとき,
が偶数のとき, の範囲で,
の範囲で,
![Rendered by QuickLaTeX.com \therefore\left\{\min_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}\right\}\int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx\leqq a_k\leqq\left\{\max_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}\right\}\int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmgAAAA0AQAAAAAWR/lBAAAAAnRSTlMAAHaTzTgAAAAbSURBVEjH7cEBDQAAAMKg909tDjegAAAAgFcDD9gAAa0Y8NwAAAAASUVORK5CYII=)
ここで,
![Rendered by QuickLaTeX.com \int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx=\left[-\frac{1}{\left(2n+1\right)\pi}\cos{\left(\left(2n+1\right)\pi x\right)}\right]_{x_k}^{x_{k+1}}\bigm=\frac{\left(-1\right)^k-\left(-1\right)^{k+1}}{\left(2n+1\right)\pi}\bigm=\frac{2}{\left(2n+1\right)\pi}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmMAAABJAQAAAABZGxypAAAAAnRSTlMAAHaTzTgAAAAcSURBVFjD7cExAQAAAMKg9U/tbwagAAAAAADgDRY+AAF+KLK7AAAAAElFTkSuQmCC) (∵
(∵ は偶数)
は偶数)
また, は増加関数のため,
は増加関数のため,
![Rendered by QuickLaTeX.com \min_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}=f\left(x_k\right)](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAANAAAAAWAQAAAACZbi9wAAAAAnRSTlMAAHaTzTgAAAAOSURBVBgZYxgFo4CqAAACUgABm35oiwAAAABJRU5ErkJggg==)
![Rendered by QuickLaTeX.com \max_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}=f\left(x_{k+1}\right)](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAOYAAAAWAQAAAAD8g90PAAAAAnRSTlMAAHaTzTgAAAAOSURBVBgZYxgFo2CQAQAClAABSsOOoQAAAABJRU5ErkJggg==)
であるから,

証明終了.
(3)
 ,
, であるから,
であるから, .
.

ここで,(F1)より,

(F2)より,

辺々を足して,


ここで, より,
より,

よって,はさみうちの原理より,

証明終了.
(4)
ナ:
解説
(1)
 (
( は整数)
は整数)
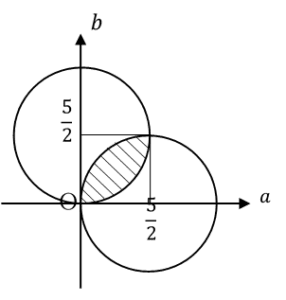
区間![Rendered by QuickLaTeX.com \left[0,1\right]](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAACEAAAATAQAAAAA2LVlkAAAAAnRSTlMAAHaTzTgAAAALSURBVAgdY6A7AAAAcgABQQ/ysgAAAABJRU5ErkJggg==) に属するならば,
に属するならば,


よって,求める個数は 個……(答)
個……(答)
 を順番に代入すると,
を順番に代入すると,

であることが分かる.
 ……(答)
……(答)(4)
 と定義すれば,(F1)と同様に,
と定義すれば,(F1)と同様に,

が成り立つ.
また,

と書ける.
以上より,


が成り立つ.
一方,区分求積法の考え方を用いれば,


よって,はさみうちの原理より
 ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。







![Rendered by QuickLaTeX.com \therefore\left\{\min_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}\right\}\int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx\leqq a_k\leqq\left\{\max_{\left[x_k,x_{k+1}\right]}{f\left(x\right)}\right\}\int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-f36be33140d882a415e9c83b4517d00d_l3.png)
![Rendered by QuickLaTeX.com \int_{x_k}^{x_{k+1}}\sin{\left(\left(2n+1\right)\pi x\right)}dx=\left[-\frac{1}{\left(2n+1\right)\pi}\cos{\left(\left(2n+1\right)\pi x\right)}\right]_{x_k}^{x_{k+1}}\bigm=\frac{\left(-1\right)^k-\left(-1\right)^{k+1}}{\left(2n+1\right)\pi}\bigm=\frac{2}{\left(2n+1\right)\pi}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-c2feed9a41ae6737010103dd006acf33_l3.png) (∵
(∵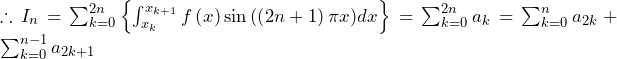
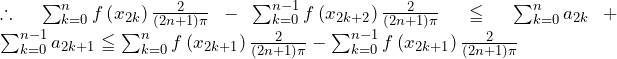
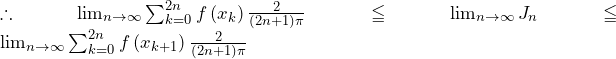
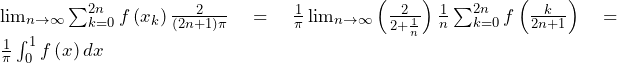
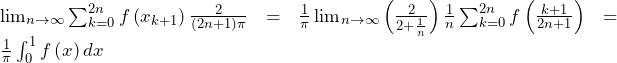

 ……(答)
……(答)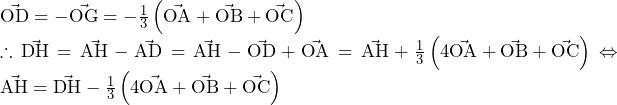
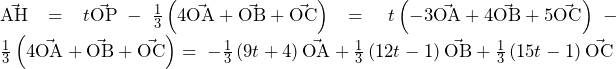 ……(答)
……(答)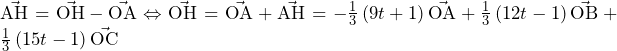
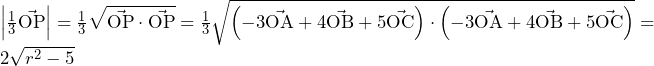
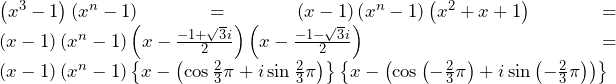
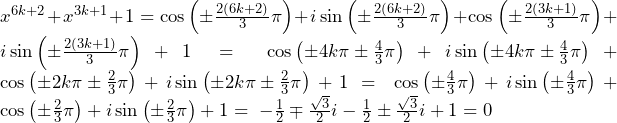
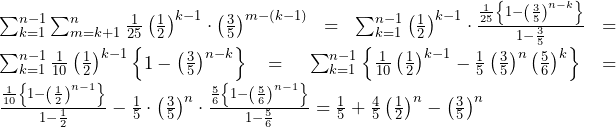 ……(答)
……(答)