2017年慶應義塾大学総合政策|過去問徹底研究 大問6 方針の立て方 (1) どの工場にも自由度はないため,そのものを塊と見て考える.素直に定義に従って計算すれば,特に難しい解法の必要はない. (2) 工場の汲み上げ量が自由度を持つため,他の工場の汲み上げ量の総和とで分離して考えることにしよう.する
- …続きを読む
-
2017年慶應義塾大学総合政策|過去問徹底研究 大問6
方針の立て方
(1)
どの工場にも自由度はないため, そのものを塊と見て考える.素直に定義に従って計算すれば,特に難しい解法の必要はない.
そのものを塊と見て考える.素直に定義に従って計算すれば,特に難しい解法の必要はない.
(2)
工場 の汲み上げ量が自由度を持つため,他の工場の汲み上げ量の総和
の汲み上げ量が自由度を持つため,他の工場の汲み上げ量の総和 と
と で分離して考えることにしよう.すると,
で分離して考えることにしよう.すると, は2文字の関数となるため一文字固定法の考え方で解いていこう.
は2文字の関数となるため一文字固定法の考え方で解いていこう.解答例
(55)(56)(57)(58)(59)(60)(61)(62)……
(63)(64)(65)(66)(67)(68)(69)(70)……
解説
(1)

 のとき,
のとき, ……(答)
……(答)(2)
 とすると,
とすると,

となる.工場 の利益は,
の利益は,

 で,
で,
ここで, より,
より,
両辺を で総和を取ると,左辺は
で総和を取ると,左辺は に依存しないから,
に依存しないから,


 ……(答)
……(答)







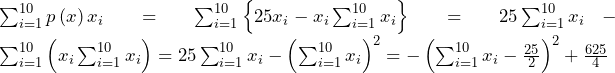
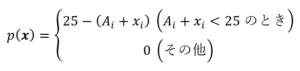

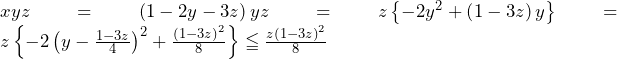
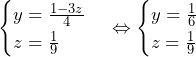
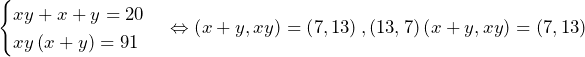 について.
について.