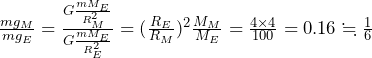物体の運動について考えるとき、v–tグラフをかくととても便利です! このページでは、v–tグラフの描き方、意味を説明していきます。 v-tグラフの意味と読み取り方を中心に~ 力学の最初の方に出てくるv – tグラフについて苦手な方が多いのでまとめてみます。 まず以
- …続きを読む
- [speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]物理、高校に入ってから数学みたいになってきてよく分からない。[/speech_bubble]
[speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]えっどういうこと?[/speech_bubble]
[speech_bubble type="ln-flat" subtype="L1" icon="seitom3.gif" name="小山くん"]この間v-tグラフとかでてきたじゃん〜[/speech_bubble]
[speech_bubble type="ln-flat" subtype="R1" icon="seitow4.gif" name="山田さん"]あれね、どうしてあんなグラフとか描く必要があるのかしら。[/speech_bubble]
物体の運動について考えるとき、v–tグラフをかくととても便利です!
このページでは、v–tグラフの描き方、意味を説明していきます。v-tグラフの意味と読み取り方を中心に~
力学の最初の方に出てくるv – tグラフについて苦手な方が多いのでまとめてみます。
まず以下のことを理解して覚えてください
①v –tグラフの傾き:加速度を表す。
②v –tグラフの面積:移動距離を表す。
まず①について説明します。等加速度運動の式v = v0 + atにおいて、時間tについてのグラフと見ると傾きがaだとわかると思います。
(y = ax +bでaは傾きですよね)また物理において時間t > 0になることが通常ないので、たいていの場合はt = 0から始まります。そのため切片v0は初速度だということもわかります
(y = ax + bでbは切片ですよね)②については小学生の時にこのようなことを考えませんでしたか?

このとき(道のり) = (速さ) × (時間)が成り立ちました。v –tグラフでは縦軸速さv、横軸時間tなので、今回のようなvが一定のグラフにおいて
(面積) = (縦) × (横) = (速さ) × (時間) (1)
が成り立ちます。

速さ一定ではなく時間変化するとしても考える時間幅をとても小さくしたら(1)式は成立します。
これは数学的には積分の考えです。実際に
x=∫ v dt
がこのテーマの裏には隠れています。
グラフの面積の正負については、
グラフの面積>0:正方向へ移動距離
グラフの面積<0:負方向への移動距離
を表しています。
例えば下のグラフではグラフの右の図(青いボール)のような運動を表しています。


VTグラフを読み取る
物体の運動において、大事な要素は3つあります。
位置x、速度v、加速度aの3つです。
これらは、運動の種類によっては時間変化します。
それを分かりやすくするためにグラフにするのです。つまり、v–tグラフは横軸に時間t、縦軸に速度vを取ったもので、速度vと時間tがどのような関係にあるかを示したグラフになります。
また、v−tグラフの面積を計算すると、その値は変位を表します。
そして、このグラフの傾きは加速度aを表します。グラフが出てきたら以上の2つの値が決定します。
[plus url1="https://hiroacademia.jpn.com/blog/5minutes/5minbutsu/enshinryoku/』" title1="0から理解する遠心力の理屈" url2="https://hiroacademia.jpn.com/blog/5minutes/5minbutsu/kepler/" title2="0からのケプラーの法則の理解の仕方" url3="https://hiroacademia.jpn.com/blog/5minutes/5minbutsu/hennisonoiti/" title3="ベクトルとスカラーの違いは?" url4="https://hiroacademia.jpn.com/blog/5minutes/5minbutsu/toukasokusonosann/" title4="等速度運動、等加速度運動の3つの公式"]







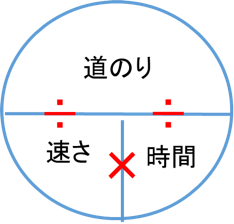
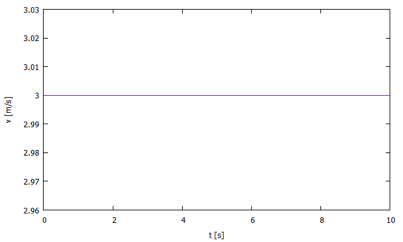
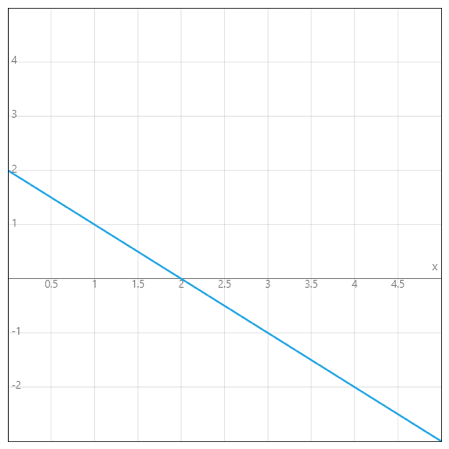
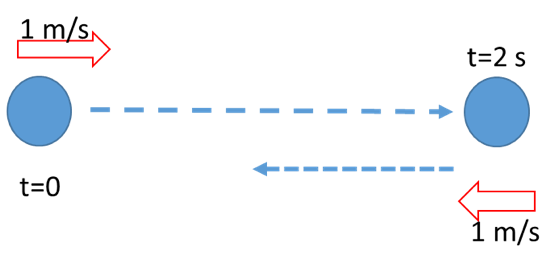
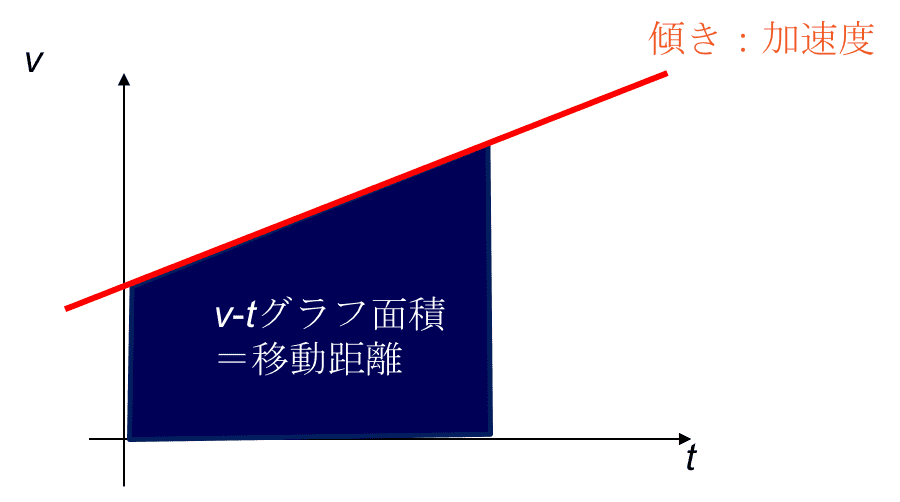



 図2
図2