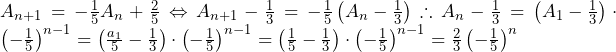2016年慶應大学総合政策数学|過去問徹底研究大問3 方針の立て方 は倍角の公式を用いればのみで表せるため,さえ求められれば良いのだと判断する. 本解冒頭ののように,(は自然数)で与えられている場合に分母を払うのは典型的な処理であるためおさえておくこと. 後は,加法定理で分解していけば求まる. 解答
- …続きを読む
-
2016年慶應大学総合政策数学|過去問徹底研究大問3
方針の立て方
 は倍角の公式を用いれば
は倍角の公式を用いれば のみで表せるため,
のみで表せるため, さえ求められれば良いのだと判断する.
さえ求められれば良いのだと判断する.
本解冒頭の のように,
のように, (
( は自然数)で与えられている場合に分母を払うのは典型的な処理であるためおさえておくこと.
は自然数)で与えられている場合に分母を払うのは典型的な処理であるためおさえておくこと.
後は,加法定理で分解していけば求まる.解答例
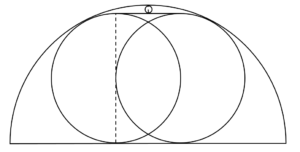
(35)(36)……10
(37)(38)……02
(39)(40)……05
(41)(42)……05解説
 より,
より,
また,加法定理を用いれば,

であるから,

加法定理より,


倍角の公式より,


これを解くと,

であるが, より,
より, より,
より,

であり,


 ……(答)
……(答)
 ……(答)
……(答)続きはこちらから

大問1
大問2
大問3
大問4
大問5
早慶の過去問を解いてみてまったくわからない・・どのように勉強をしたら良いのか知りたい方はお気軽にこちらからご連絡ください。







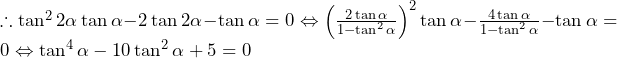
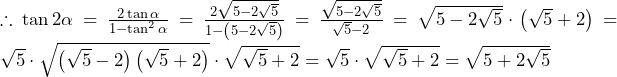
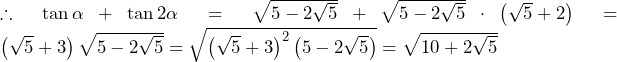 ……(答)
……(答)
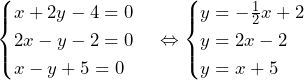

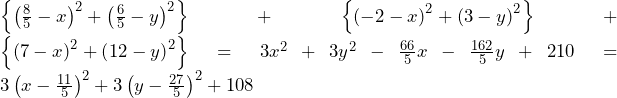
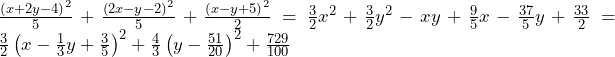
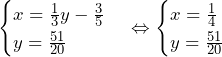
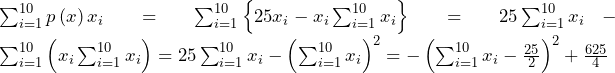
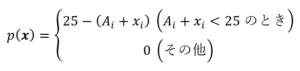
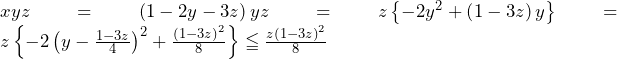
 について.
について.