慶應大学商学部数学方針の立て方 (ⅰ)は具体的に考えてみれば解答が得られる. (ⅱ)(ⅲ)は誘導に乗っていければ解説以上の特筆事項はない.コンビネーションの公式:は本問では度々使う.入試数学(特に文系数学)には必須の公式ではないが,余力のある受験生は覚えておいても良いかもしれない.この公式を覚えてな
- …続きを読む
-
慶應大学商学部数学方針の立て方
(ⅰ)は具体的に考えてみれば解答が得られる.
(ⅱ)(ⅲ)は誘導に乗っていければ解説以上の特筆事項はない.コンビネーションの公式: は本問では度々使う.入試数学(特に文系数学)には必須の公式ではないが,余力のある受験生は覚えておいても良いかもしれない.この公式を覚えてなくとも本問では回答欄の形式から,どう変形していけば良いかが分かる.
は本問では度々使う.入試数学(特に文系数学)には必須の公式ではないが,余力のある受験生は覚えておいても良いかもしれない.この公式を覚えてなくとも本問では回答欄の形式から,どう変形していけば良いかが分かる.解答例
(ⅰ)
(45)
(46)
(47)(48)
(49)
(50)
(51)(52)
(53)(54)
(55)(56)
(57)(58)
(ⅱ)
(59)
(60)
(61)
(62)
(63)
(64)
(65)
(66)
(67)
(68)
(69)
(70)
(71)
(72)
(73)
(74)
(75)
(76)
(77)
(ⅲ)
(ア)
(イ)
(ウ)
(エ)
(オ)
(カ)
(キ)
(ク)
(ケ)
(コ)
(サ)
(シ)
解説
(ⅰ)
客3の待ち時間は0,5,10分のいずれか.



よって,
 ……(答)
……(答)
客4の待ち時間は0,5,10,15分のいずれか.




よって,
 ……(答)
……(答)(ⅱ)
〇(59)~(62)について
 に対して帰納法の仮定が使える.
に対して帰納法の仮定が使える. は奇数であるから,④の
は奇数であるから,④の が奇数のときが適用される.
が奇数のときが適用される.
 ……(答)
……(答)
〇(63)~(65)について
 に対して帰納法の仮定が使える.
に対して帰納法の仮定が使える. は偶数であるから,④の
は偶数であるから,④の が偶数のときが適用される.
が偶数のときが適用される.
 ……(答)
……(答)
〇(66)と(67)について
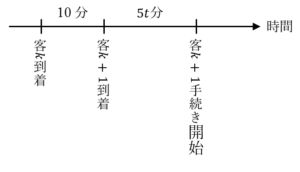
題意を満たす場合,時系列を図示すると,

上図.
Aの手続きは5分かかり,Bの手続きは15分かかることから, は,客
は,客 が
が 分待った後にAを行う確率と,客
分待った後にAを行う確率と,客 が
が 分待った後にBを行う確率の和になる.……(答)
分待った後にBを行う確率の和になる.……(答)〇(68)~(72)について
 は,④で
は,④で としたものと考える.すると
としたものと考える.すると が奇数のときが適用される.
が奇数のときが適用される.
 ……(答)
……(答)
これらを⑤に代入すれば,
 ……(答)
……(答)
(※最後の式変形の際, を用いた)
を用いた)
〇(73)~(77)について
 は,④で
は,④で としたものと考える.すると
としたものと考える.すると が偶数のときが適用される.
が偶数のときが適用される.
 ……(答)
……(答)
これらを⑤に代入すれば,
 ……(答)
……(答)(ⅲ)
〇(ア)~(ウ)について
 は④の
は④の のパターンであり,
のパターンであり, が奇数,偶数のときが適用される.
が奇数,偶数のときが適用される.
 ……(答)
……(答)
〇(エ)について
 ……(答)
……(答)
〇(オ)~(キ)について
(エ)の結果より である.
である.
(ア)~(ウ)の結果を⑥に代入して,
 ……(答)
……(答)
(※最後の式変形の際, を用いた)
を用いた)
〇(ク)~(ケ)について
 は④の
は④の のパターンであり,
のパターンであり, が偶数,奇数のときが適用される.
が偶数,奇数のときが適用される.
 ……(答)
……(答)
〇(コ)と(サ)について
(ク)~(ケ)の結果を⑥に代入して,
 ……(答)
……(答)
〇(シ)について
 は
は のときの中でも,(ⅱ)で考えられていなかった
のときの中でも,(ⅱ)で考えられていなかった のときである.……(答)
のときである.……(答)







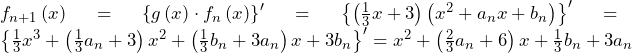
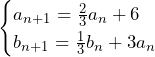 ……(答)
……(答)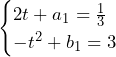
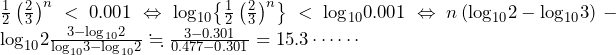
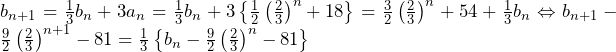
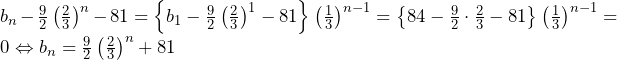 ……(答)
……(答)
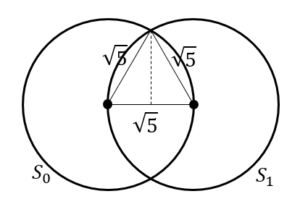
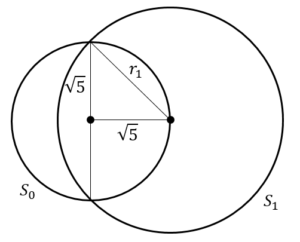
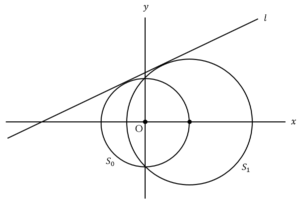
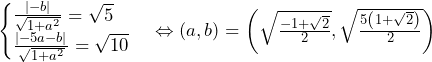
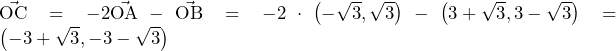
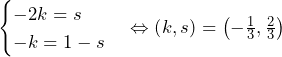
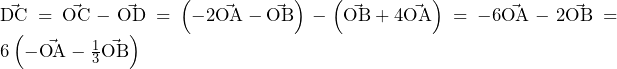
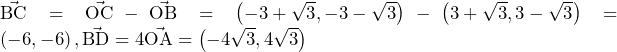 より,
より,