方針の立て方 (1) 実際に題意を満たすサイコロを目の出し方を考えることで方針を得る.複数のサイコロの問題ではサイコロは区別したほうが処理しやすい. (2) 「少なくとも」の問題であるため,基本解法である余事象で解くと考える.後は全問と同様に題意を満たすサイコロの目の出し方を考えれば,解答を得られる
- …続きを読む
-
方針の立て方
(1)
実際に題意を満たすサイコロを目の出し方を考えることで方針を得る.複数のサイコロの問題ではサイコロは区別したほうが処理しやすい.(2)
「少なくとも」の問題であるため,基本解法である余事象で解くと考える.後は全問と同様に題意を満たすサイコロの目の出し方を考えれば,解答を得られる.(3)
これも題意を満たすパターンを考えることで方針を得られる.解答例
(1)(2)(3)(4)……

(5)(6)(7)(8)……
(9)(10)(11)(12)(13)(14)……
解説
サイコロを区別して考え,一つ目のサイコロの目が
 ,二つ目のサイコロの目が
,二つ目のサイコロの目が であったとき,この目の出方を
であったとき,この目の出方を と表す.
と表す.
(1)
題意を満たすサイコロの目の出し方は, とこれらを入れ替えた計8通り.全ての目の出し方は
とこれらを入れ替えた計8通り.全ての目の出し方は 通りのため,求める確率は,
通りのため,求める確率は,
 ……(答)
……(答)(2)
余事象で考える.36通りの目の出し方の中で,差が1か2となる出し方は, とこれらを入れ替えた計18通りであり,これらを除いた18通りの目の出し方を2回すれば余事象の条件が満たされる.よって,余事象の確率は,
とこれらを入れ替えた計18通りであり,これらを除いた18通りの目の出し方を2回すれば余事象の条件が満たされる.よって,余事象の確率は,

である.よって,求める確率は,
 ……(答)
……(答)(3)
箱1の玉を取り出す事象を①,箱2の玉を取り出す事象を②,それ以外の箱を確認する事象を③と表すことにする.1回の操作で,①が起こる確率は ,②が起こる確率は
,②が起こる確率は ,③が起こる確率は
,③が起こる確率は である.
である.
題意を満たすパターンは,「○12」,「○21」,「1○2」,「2○1」,「112」,「221」の6通りであり,前4つが起こる確率はそれぞれ であり,「112」が起こる確率は
であり,「112」が起こる確率は ,「221」が起こる確率は
,「221」が起こる確率は である.よって,求める確率は,
である.よって,求める確率は,
 ……(答)
……(答)







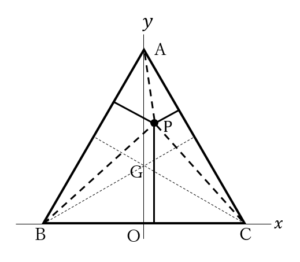
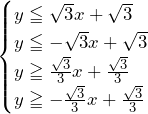
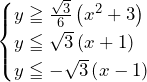
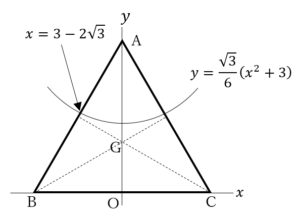
![Rendered by QuickLaTeX.com 2\int_{3-2\sqrt3}^{0}\left\{\left(\sqrt3x+\sqrt3\right)-\left(\frac{\sqrt3}{6}x^2+\frac{\sqrt3}{2}\right)\right\}dx=\left[-\frac{\sqrt3}{9}x^3+\sqrt3x^2+\sqrt3x\right]_{3-2\sqrt3}^0=16-9\sqrt3](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-ca7e2526c667d1ae7bb1ab5fab12914c_l3.png) ……(答)
……(答)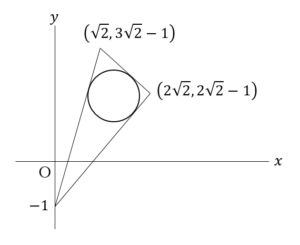
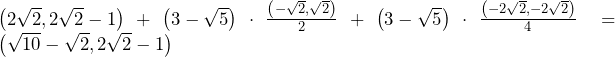 ……(答)
……(答)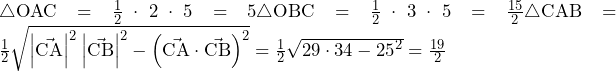 より,
より,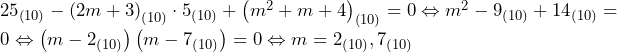
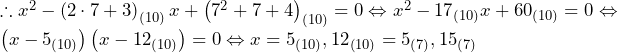
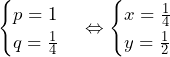 でとり,値を大きくするとある
でとり,値を大きくするとある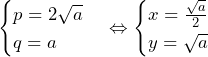 の両方でとり,それより
の両方でとり,それより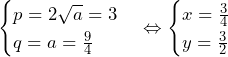 のとき,
のとき,