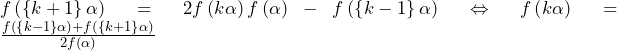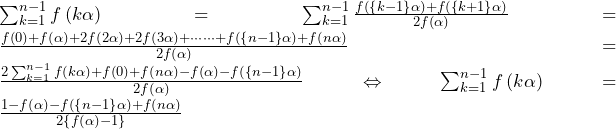方針の立て方 (1) 上の点,上の点の両方を動かして解析しようとするととても複雑になる.そこで,題意を満たすのはどのような線分なのかを定性的に考える.すると,点からに垂線を引いたときを考えれば良いと分かる. (2) まずは,図を描いてみて情報を整理する. 円や球の接点に関する議論は,基本的には半径と
- …続きを読む
-
方針の立て方
(1)
 上の点,
上の点, 上の点の両方を動かして解析しようとするととても複雑になる.そこで,題意を満たすのはどのような線分なのかを定性的に考える.すると,点
上の点の両方を動かして解析しようとするととても複雑になる.そこで,題意を満たすのはどのような線分なのかを定性的に考える.すると,点 から
から に垂線を引いたときを考えれば良いと分かる.
に垂線を引いたときを考えれば良いと分かる.(2)
まずは,図を描いてみて情報を整理する.
円や球の接点に関する議論は,基本的には半径と接線が直交することを応用して,内積が0となることを利用する.本問もそれを使おうと考える.すると,点 についてはそれで上手くいくが,点
についてはそれで上手くいくが,点 は
は と直交するベクトルの情報を出すことが難しい.そこで,別の図形的性質がないかを考える.すると,
と直交するベクトルの情報を出すことが難しい.そこで,別の図形的性質がないかを考える.すると, と
と が平行であることが見つかるから,内積0の代わりにこれを使えばよいと分かる.
が平行であることが見つかるから,内積0の代わりにこれを使えばよいと分かる.
後は と
と の座標を文字を使って表し,解析していく.
の座標を文字を使って表し,解析していく.(3)
直円錐 の体積を出すには,底面の半径と高さの情報が必要になると考える.底面の半径も高さも直接出すのは難しい(球面
の体積を出すには,底面の半径と高さの情報が必要になると考える.底面の半径も高さも直接出すのは難しい(球面 が
が 内の半端な位置にいるために難しい)から,分割して考える.前問で点
内の半端な位置にいるために難しい)から,分割して考える.前問で点 ,
, の座標を求めさせたことから,点
の座標を求めさせたことから,点 ,
, の箇所で分割(
の箇所で分割( と
と に分割)して考える.すると三角形
に分割)して考える.すると三角形 で考えるという方針が立つ.
で考えるという方針が立つ. については,(1)の議論や前問で得た「
については,(1)の議論や前問で得た「 と
と が平行である」という知見を考えれば,
が平行である」という知見を考えれば, に変換して考えることが思いつく.すると,高さについては点
に変換して考えることが思いつく.すると,高さについては点 で分割(
で分割( と
と に分割)して考えるという方針が立つ.
に分割)して考えるという方針が立つ.解答例
球面
 の方程式は
の方程式は である.
である.
(1)
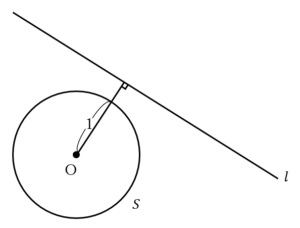
題意を満たす 上の点は,原点から直線
上の点は,原点から直線 に下ろした垂線(つまり,中心と直線の最短距離)と球面
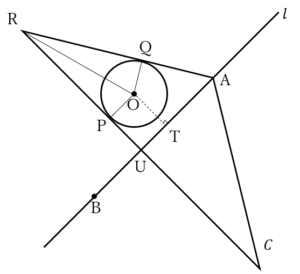
に下ろした垂線(つまり,中心と直線の最短距離)と球面 との交点である(下図).
との交点である(下図).

 の方程式は,実数
の方程式は,実数 を用いて
を用いて と書ける.
と書ける.
よって,原点と 上の点との距離は,
上の点との距離は,

と書ける. は
は のとき最小値
のとき最小値 を取るから,原点と
を取るから,原点と 上の点を結ぶ線分の長さの最小値は,
上の点を結ぶ線分の長さの最小値は, である.
である.
よって, 上の点と
上の点と 上の点を結ぶ線分の長さの最小値は,
上の点を結ぶ線分の長さの最小値は, の半径が1であることから,
の半径が1であることから, ……(答)
……(答)(2)

〇点 の座標
の座標
線分 と
と は平行であるため,実数
は平行であるため,実数 を用いて
を用いて とおける.
とおける.
また,点 は
は 上の点であるから,
上の点であるから,

 の方向と
の方向と の方向は等しいため,
の方向は等しいため, が適当.
が適当.
 ……(答)
……(答)
〇点 の座標
の座標
 (
( は実数)と表せる.
は実数)と表せる.
点 は
は 上の点であるため,
上の点であるため,
 ……①
……①
また, より,
より, である.
である. であるから,
であるから,
 ……②
……②
①②を連立すれば,
 (複号同順)
(複号同順)
となる.
 と
と の方向を考えれば,
の方向を考えれば, であるから,
であるから,

が適当.
 ……(答)
……(答)(3)

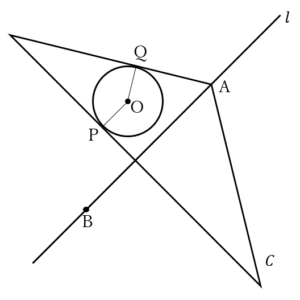
上図のように点 ,
, ,
, を取る.
を取る.
 と
と は
は の半径に当たるから,
の半径に当たるから, である.
である.

また,前問の結果より であるから,
であるから,

これらより,

 より,
より,


よって,

ところで,線分 (図中の点線)の長さは(1)の途中で求めた原点と
(図中の点線)の長さは(1)の途中で求めた原点と 上の点との距離と等しく
上の点との距離と等しく である.また,
である.また, である.
である.
よって, の底面の半径(
の底面の半径( )は,
)は,

となる.更に線分 の長さは6であるから,三平方の定理より,
の長さは6であるから,三平方の定理より,

である.また, であるから,
であるから, の高さ(
の高さ( )は,
)は,

よって,求める体積は,
 ……(答)
……(答)








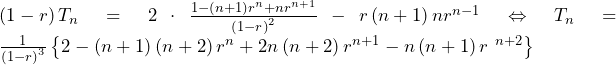 ……(答)
……(答)![Rendered by QuickLaTeX.com \int_{0}^{2}\left(-6x+15\right)dx=\left[-3x^2+15x\right]_0^2=18,\int_{0}^{2}\left(-3x^2+12\right)dx=\left[-x^3+12x\right]_0^2=16](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-c3bfa33edb30774157f6fafbfffed269_l3.png)
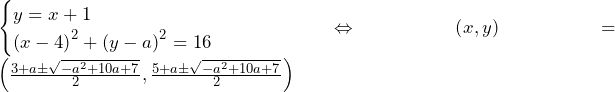 (複号同順)
(複号同順)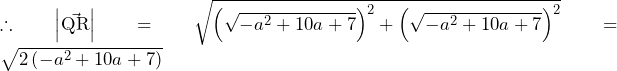
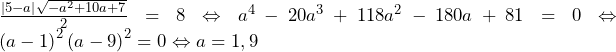 ……(答)
……(答)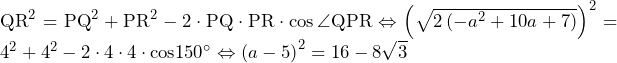 ……(答)
……(答)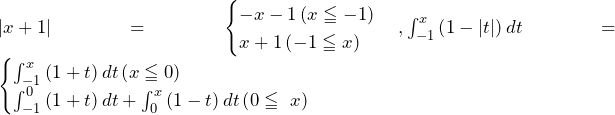 となる.
となる.![Rendered by QuickLaTeX.com F\left(x\right)=x+1+\int_{-1}^{0}\left(1+t\right)dt+\int_{0}^{x}\left(1-t\right)dt=x+1+\left[t+\frac{1}{2}t^2\right]_{-1}^0+\left[t-\frac{1}{2}t^2\right]_0^x=-\frac{1}{2}x^2+2x+\frac{3}{2}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-41c71a6f673b63fa745fc3d548c4ed52_l3.png)
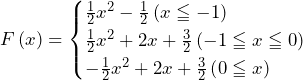 ……(答)
……(答)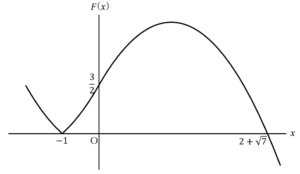
![Rendered by QuickLaTeX.com \int_{-1}^{0}\left(\frac{1}{2}x^2+2x+\frac{3}{2}\right)dx+\int_{0}^{2+\sqrt7}\left(-\frac{1}{2}x^2+2x+\frac{3}{2}\right)dx=\left[\frac{1}{6}x^3+x^2+\frac{3}{2}x\right]_{-1}^0+\left[-\frac{1}{6}x^3+x^2+\frac{3}{2}x\right]_0^{2+\sqrt7}=\frac{19+7\sqrt7}{3}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-49c0c64db15f48db2771431bf99b4c3e_l3.png) ……(答)
……(答)
 ……(答)
……(答)
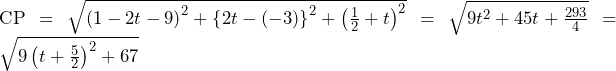
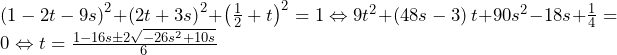
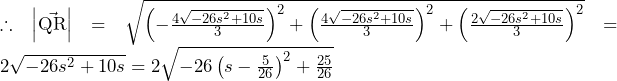
 ……(答)
……(答)