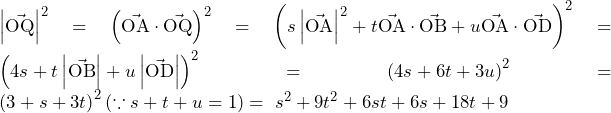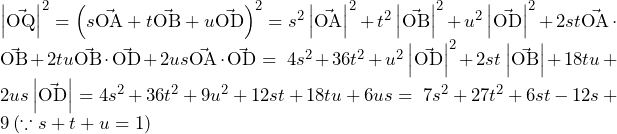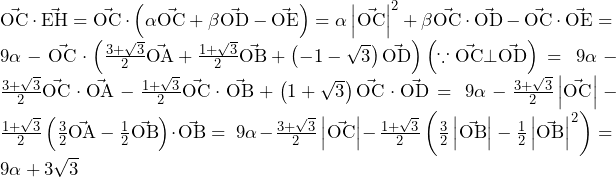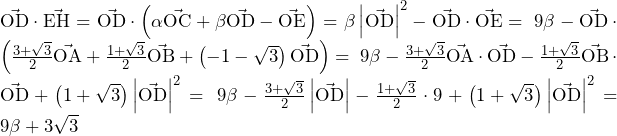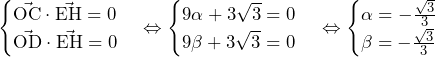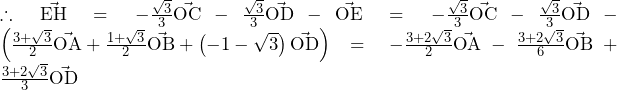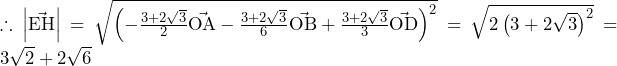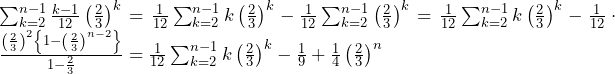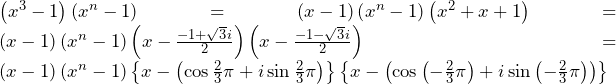方針の立て方 (1) (サ)については特筆事項なし. (シ)との関係を問われているため,の形を具体的に書き下してみると方針を得やすい.すると,が必要だと分かるため,部分積分の際にの項を微分すればよいと分かる. (2)前問で漸化式を求めたので,漸化式を利用することを考える.本解答のような漸化式を用いて
- …続きを読む
-
方針の立て方
(1)
(サ)については特筆事項なし.
(シ) と
と の関係を問われているため,
の関係を問われているため, の形を具体的に書き下してみると方針を得やすい.すると,
の形を具体的に書き下してみると方針を得やすい.すると, が必要だと分かるため,部分積分の際に
が必要だと分かるため,部分積分の際に の項を微分すればよいと分かる.
の項を微分すればよいと分かる.(2)前問で漸化式を求めたので,漸化式を利用することを考える.本解答のような漸化式を用いて
 や
や まで下げる解法は頻出のためおさえておこう.
まで下げる解法は頻出のためおさえておこう.(3)極限値が1と与えられているため,
 で考える.(※
で考える.(※ を直接示す方針でも間違いではないが,はさみうちの原理が使いにくくなる.)変形をしていくと
を直接示す方針でも間違いではないが,はさみうちの原理が使いにくくなる.)変形をしていくと の評価が必要になる.一項差のため,まずは前問(2)の結果を使おうと試みるが,前問は積(二項の掛け算)の形であるため使えない.そこで,(1)の(シ)の結果なら,分数の形を作り出せると考え,
の評価が必要になる.一項差のため,まずは前問(2)の結果を使おうと試みるが,前問は積(二項の掛け算)の形であるため使えない.そこで,(1)の(シ)の結果なら,分数の形を作り出せると考え, を
を か
か に変形することを考える.
に変形することを考える.(4)
 のままでは解法が思い浮かばないため,一先ず変形して
のままでは解法が思い浮かばないため,一先ず変形して とする.二項の掛け算の形が出てきているため,(2)の結果を使うという方針が立つ.(※(2)の結果をここまで使っていないので,(2)の結果を使うのではと疑うことでも方針が立つ.)
とする.二項の掛け算の形が出てきているため,(2)の結果を使うという方針が立つ.(※(2)の結果をここまで使っていないので,(2)の結果を使うのではと疑うことでも方針が立つ.)解答例
(1)
サ:
シ:
(2)
ス:
(3)

ここで, の範囲で,
の範囲で, であるから,
であるから, であり,積分区間
であり,積分区間 で,等号は常に成立しないことから,
で,等号は常に成立しないことから,

が成立する.(1)の(シ)の結果と合わせると,

よって,

であり,はさみうちの原理より,

これは,数列 が1に収束することに他ならない.
が1に収束することに他ならない.
証明終了.
(4)
セ:
解説
(1)
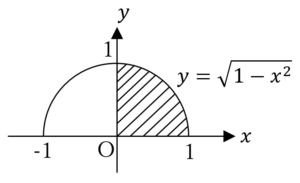
〇 (サについて)
(サについて)

これは,下図斜線部に示した四分円の面積を表す.

 ……(答)
……(答)
〇 (シについて)
(シについて)
![Rendered by QuickLaTeX.com a_n=\int_{0}^{1}\left(1-x^2\right)^\frac{n}{2}dx=\int_{0}^{1}{\left(x\right)^\prime\left(1-x^2\right)^\frac{n}{2}}dx=\left[x\left(1-x^2\right)^\frac{n}{2}\right]_0^1-\int_{0}^{1}{x\cdot\frac{n}{2}\left(1-x^2\right)^\frac{n-2}{2}\cdot\left(-2x\right)}dx=n\int_{0}^{1}{x^2\left(1-x^2\right)^\frac{n-2}{2}}dx](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmgAAABHAQAAAACb8YYuAAAAAnRSTlMAAHaTzTgAAAAcSURBVFjD7cExAQAAAMKg9U9tDB+gAAAAAAD4GBWiAAFSuDK+AAAAAElFTkSuQmCC)

一方で,

 ……(答)
……(答)(2)
前問の結果より,

(ⅰ) が偶数のとき,
が偶数のとき,

ここで,
![Rendered by QuickLaTeX.com a_2=\int_{0}^{1}\left(1-x^2\right)dx=\left[x-\frac{1}{3}x^3\right]_0^1=\frac{2}{3}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAATMAAAAcAQAAAAAlrmWkAAAAAnRSTlMAAHaTzTgAAAARSURBVBgZYxgFo2AUjAIaAQAEYAABq9PfAwAAAABJRU5ErkJggg==)

より,

(ⅱ) が奇数のとき,
が奇数のとき,

ここで,

![Rendered by QuickLaTeX.com a_0=\int_{0}^{1}1dx=\left[x\right]_0^1=1](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAALgAAAAbAQAAAADnwHgqAAAAAnRSTlMAAHaTzTgAAAAOSURBVBgZYxgFo2AQAAACiAABHLXt4gAAAABJRU5ErkJggg==)
より,

以上,(ⅰ)と(ⅱ)より,
 ……(答)
……(答)(4)
前問の結果より,

である.これより,
 ……(答)
……(答)








![Rendered by QuickLaTeX.com a_n=\int_{0}^{1}\left(1-x^2\right)^\frac{n}{2}dx=\int_{0}^{1}{\left(x\right)^\prime\left(1-x^2\right)^\frac{n}{2}}dx=\left[x\left(1-x^2\right)^\frac{n}{2}\right]_0^1-\int_{0}^{1}{x\cdot\frac{n}{2}\left(1-x^2\right)^\frac{n-2}{2}\cdot\left(-2x\right)}dx=n\int_{0}^{1}{x^2\left(1-x^2\right)^\frac{n-2}{2}}dx](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-3383a4e3a41de53f568ac6beddb7b89b_l3.png)
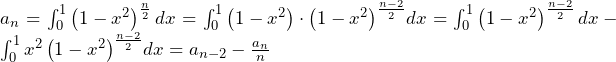
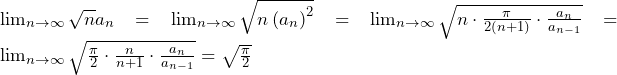 ……(答)
……(答)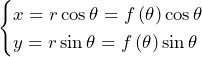
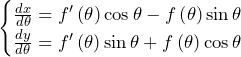
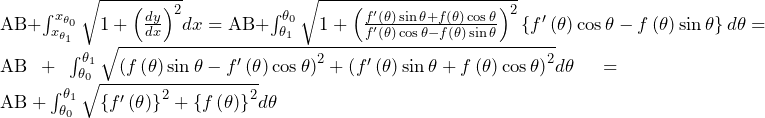
![Rendered by QuickLaTeX.com \mathrm{AB}+\int_{\theta_0}^{\theta_1}\sqrt{\left\{f^\prime\left(\theta\right)\right\}^2+\left\{f\left(\theta\right)\right\}^2}d\theta=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}\sqrt{\left\{\alpha\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2+\left\{\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right\}^2}d\theta\bigm=\frac{v}{\sqrt{v^2-1}}+\int_{\frac{\pi}{2}}^{\theta_1}{\sqrt{1+\alpha^2}\beta e^{\alpha\left(\theta-\frac{\pi}{2}\right)}}d\theta=\frac{v}{\sqrt{v^2-1}}+\sqrt{1+\alpha^2}\beta\left[\frac{1}{\alpha}e^{\alpha\left(\theta-\frac{\pi}{2}\right)}\right]_{\frac{\pi}{2}}^{\theta_1}\bigm=\frac{v}{\sqrt{v^2-1}}-\frac{\beta}{\alpha}\sqrt{1+\alpha^2}+\frac{\beta}{\alpha}\sqrt{1+\alpha^2}e^{\alpha\left(\theta_1-\frac{\pi}{2}\right)}](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-3251c46fb035b1c6f3d900fd751c1cf5_l3.png)
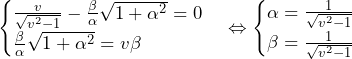 ……(答)
……(答)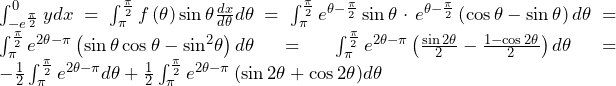
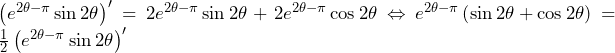
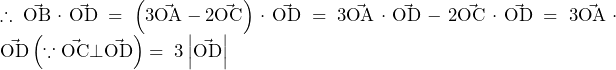 (
(