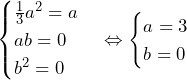方針の立て方 (1) 実際にを求めていくことで解答を得られる. (2) 前問での議論で,には周期性があることが分かる.更に,大事なのはとのなす角であることも分かるだろう(もし前問の議論だけでは方針を得られない場合には,他の具体的な組み合わせで考えてみると良い).そこで,とのなす角で場合分けをして議論
- …続きを読む
- 方針の立て方
(1)
実際に を求めていくことで解答を得られる.
を求めていくことで解答を得られる.
(2)
前問での議論で, には周期性があることが分かる.更に,大事なのは
には周期性があることが分かる.更に,大事なのは と
と のなす角であることも分かるだろう(もし前問の議論だけでは方針を得られない場合には,他の具体的な組み合わせで考えてみると良い).そこで,
のなす角であることも分かるだろう(もし前問の議論だけでは方針を得られない場合には,他の具体的な組み合わせで考えてみると良い).そこで, と
と のなす角で場合分けをして議論していけば良いと判断する.
のなす角で場合分けをして議論していけば良いと判断する.解答例
(1)

(ⅰ)と(ⅱ)に従って を求めていくと,上図のようになる.
を求めていくと,上図のようになる.
上図より であるから,求める
であるから,求める は
は ……(答)
……(答)(2)
 として,前問の議論(
として,前問の議論( のとき)をまとめると,下表のようになる.
のとき)をまとめると,下表のようになる.

































これより,
 の値は
の値は という周期9の並びを繰り返すことが分かる.
という周期9の並びを繰り返すことが分かる.
 となる
となる が存在するため
が存在するため は題意を満たさない.
は題意を満たさない.
以下, として,
として, のみを考える.更に
のみを考える.更に と
と のなす角の内,小さい方を
のなす角の内,小さい方を と表す.
と表す.
(Ⅰ) となる
となる のとき
のとき
実際に を求めていくと,
を求めていくと, のときのように
のときのように の値は周期9の並びを繰り返し,
の値は周期9の並びを繰り返し, は1から9の全ての値をとる.よって,題意を満たさない.
は1から9の全ての値をとる.よって,題意を満たさない.
(Ⅱ) となる
となる のとき
のとき
実際に を求めていく.例えば
を求めていく.例えば の場合,
の場合,

上図のようになる.
 としてまとめると,下表のようになる.
としてまとめると,下表のようになる.



























これより,
 の値は
の値は という周期9の並びを繰り返すことが分かる.
という周期9の並びを繰り返すことが分かる.
 となる
となる が存在するため
が存在するため は題意を満たさない.また,他の
は題意を満たさない.また,他の についても同様に題意を満たさない.
についても同様に題意を満たさない.
(Ⅲ) となる
となる のとき
のとき
実際に を求めていく.例えば
を求めていく.例えば の場合,
の場合,

上図のようになる.
 としてまとめると,下表のようになる.
としてまとめると,下表のようになる.















これより,
 の値は
の値は という周期3の並びを繰り返すことが分かる.
という周期3の並びを繰り返すことが分かる.
 となる
となる が存在しないため
が存在しないため は題意を満たす.また,他の
は題意を満たす.また,他の についても同様に題意を満たす.
についても同様に題意を満たす.
 となる
となる の組み合わせは
の組み合わせは であり,これら6組は題意を満たす.
であり,これら6組は題意を満たす.
(Ⅳ) となる
となる のとき
のとき
実際に を求めていく.例えば
を求めていく.例えば の場合,
の場合,





























これより,
 の値は
の値は という周期9の並びを繰り返すことが分かる.
という周期9の並びを繰り返すことが分かる.
 となる
となる が存在するため
が存在するため は題意を満たさない.また,他の
は題意を満たさない.また,他の についても同様に題意を満たさない.
についても同様に題意を満たさない.
以上,(Ⅰ)~(Ⅳ)より,題意を満たす の組み合わせは
の組み合わせは の範囲でも題意を満たす
の範囲でも題意を満たす の組み合わせは6組あるので,求める個数は
の組み合わせは6組あるので,求める個数は 個……(答)
個……(答)






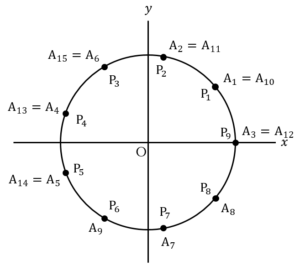

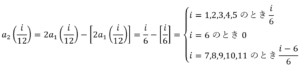
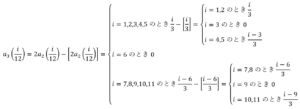
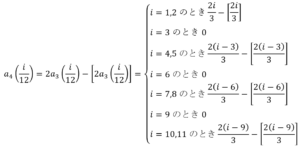
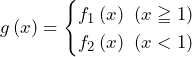
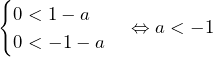 のとき
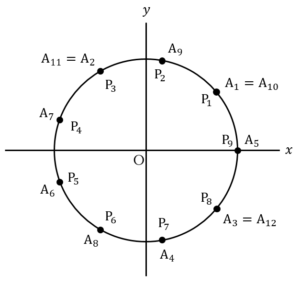
のとき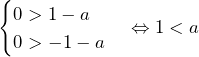 のとき
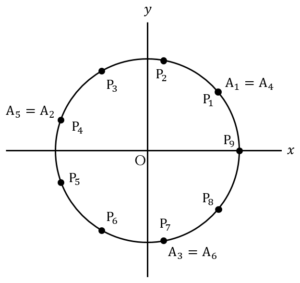
のとき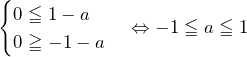 のとき
のとき
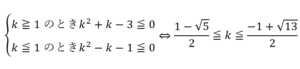
![Rendered by QuickLaTeX.com \int_{0}^{x}\left\{P\left(t\right)\right\}^mdt=\int_{0}^{x}\left\{at+b\right\}^2dt=\left[\frac{1}{3}a^2t^3+abt^2+b^2t\right]_0^x=\frac{1}{3}a^2x^3+abx^2+b^2x P\left(x^3\right)-P\left(0\right)=\left(ax^3+b\right)-b=ax^3](https://hiroacademia.jpn.com/wp/wp-content/ql-cache/quicklatex.com-a11b033768caae58621300cc339f8d26_l3.png)